Содержание
- 2. Определение 1 Множество А называется подмножеством В, если для любого х ( ) Обозначение: Другими словами,
- 3. Доказательство Для доказательства а) надо убедиться в истинности высказывания , но оно очевидным образом истинно, так
- 4. Конечно, теорема 2 интуитивно очевидна, но если мы, кроме очевидности, стремимся еще и к строгости, то
- 5. Определение 3 Множества А и В называются равными, если они состоят из одних и тех же
- 6. Пример 1 {a, b, c, d} = {c, d, a, b}. Пример 2 {a, b, c,
- 7. Таким образом, для того, чтобы доказать равенство множеств А и В, надо доказать два включения: и
- 8. Отметим, что понятия элемента и множества довольно условны. Один и тот же объект в одной ситуации
- 9. 2. Операции объединения и пересечения Определение 1 Объединением двух множеств А и В называется множество .
- 10. Доказательство а) Возьмем . При последнем переходе мы воспользовались идемпотентностью дизъюнкции. Таким образом, идемпотентность объединения в
- 11. Следовательно, . г) Возьмем , так как высказывание тождественно ложно. Следовательно, . д) Если , то
- 12. Теорема 3 Пусть А, В – произвольные множества, тогда: а) ; б) . Доказательство а) Возьмем
- 13. Докажем второе включение. Возьмем , так как , . Следовательно, . Теорема доказана. Определение 4 Пересечением
- 14. Теорема 5 Пусть А, В, С – произвольные множества, тогда: а) - идемпотентность пересечения; б) -
- 15. Следовательно, . в) Возьмем Следовательно, . г) , так как – тождественно ложное высказывание. Теорема 6
- 16. б) . Доказательство а) Возьмем , то есть . б) Пусть . Возьмем , то есть
- 17. Теорема 7 (дистрибутивные законы) Пусть А, В, С – произвольные множества, тогда: а) – дистрибутивность пересечения
- 18. 3. Разность множеств, дополнение, симметрическая разность Определение 1 Разностью множеств называется множество . Пример Пусть А={1,3,4,7,8,9,10},
- 19. б) Пусть . Возьмем , так как , то , значит , то есть . Теперь
- 20. Теорема 3 (законы Моргана) а) ; б) . Доказательство а) Возьмем
- 21. б) Возьмем Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его
- 22. Довольно часто под универсальным множеством понимают множество R –– множество вещественных чисел или множество С –
- 24. Скачать презентацию

















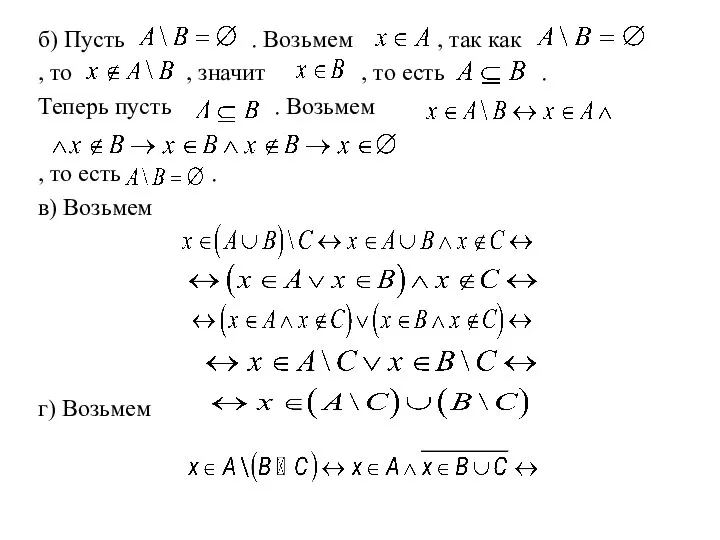



 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Классификация уровней понимания
Классификация уровней понимания Сложение и вычитание в пределах 1000
Сложение и вычитание в пределах 1000 Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Деление чисел
Деление чисел Простые и составные числа (дистант)
Простые и составные числа (дистант) Числовой луч (1 класс)
Числовой луч (1 класс) Площадь параллелограмма
Площадь параллелограмма Основы математической статистики
Основы математической статистики Линейные пространства
Линейные пространства По следам телепередач. Поле чудес
По следам телепередач. Поле чудес Степень с отрицательным показателем
Степень с отрицательным показателем Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла Координати вектора. Модуль вектора
Координати вектора. Модуль вектора Множество. Элемент множества
Множество. Элемент множества Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ  Классификация треугольников
Классификация треугольников Объёмные фигуры и формулы нахождения объёма
Объёмные фигуры и формулы нахождения объёма Нахождение дроби от числа
Нахождение дроби от числа Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Системы массового обслуживания с отказом
Системы массового обслуживания с отказом Умножение обыкновенных дробей
Умножение обыкновенных дробей Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Решение составных задач
Решение составных задач Наборы из нулей и единиц. Дискретный анализ. Лекция 2
Наборы из нулей и единиц. Дискретный анализ. Лекция 2 ВПР - 7- 9 класс
ВПР - 7- 9 класс Симметрия в пространстве. Уравнение Сферы
Симметрия в пространстве. Уравнение Сферы Финансовая грамотность
Финансовая грамотность