Содержание
- 2. Вентцель Е.С. Исследование операций: задачи, принципы, методология / Е.С. Вентцель. – М.: 1972 г. – 552
- 3. Линейное программирование Каждый человек ежедневно, не всегда осознавая это решает проблему: как получить наибольший эффект, обладая
- 4. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений.
- 5. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений.
- 6. К числу задач линейного программирования можно отнести задачи: рационального использования сырья и материалов; задачи оптимального раскроя;
- 7. Постановка задачи линейного программирования Линейной функцией n переменных x1 ,x2 ,…, xn называется функция вида Задача
- 8. Постановка задачи линейного программирования Другие постановки задачи линейного программирования могут быть сведены к данной: 1) если
- 9. Геометрический метод решения задачи линейного программирования Графическое решение задачи линейного программирования с двумя переменными и системой
- 10. Геометрический метод решения задачи линейного программирования На плоскости строим прямые для Далее определяем полуплоскости, удовлетворяющие неравенствам
- 11. Геометрический метод решения задачи линейного программирования Далее строим вектор нормали . После этого через начало вектора
- 12. Геометрический метод решения задачи линейного программирования Рассмотрим пример решения задачи линейного программирования геометрическим способом. Задача о
- 13. Геометрический метод решения задачи линейного программирования Обозначим x1 – количество выпускаемой продукции A1, x2 – количество
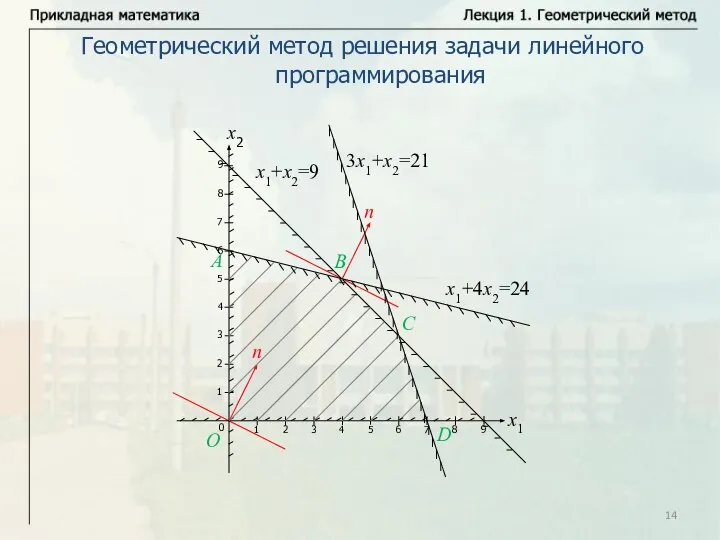
- 14. Геометрический метод решения задачи линейного программирования
- 15. Геометрический метод решения задачи линейного программирования ОДР – пятиугольник OABCD. Координаты вектора нормали соответствуют коэффициентам перед
- 16. Геометрический метод решения задачи линейного программирования Замечание. Если в условиях рассмотренной задачи то Получаем решение на
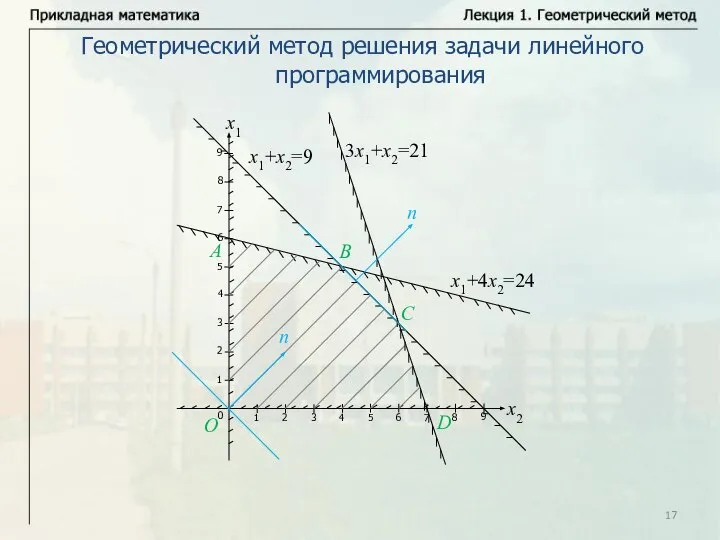
- 17. Геометрический метод решения задачи линейного программирования
- 18. Геометрический метод решения задачи линейного программирования Рассмотрим различные случаи при решении задач линейного программирования геометрическим способом.
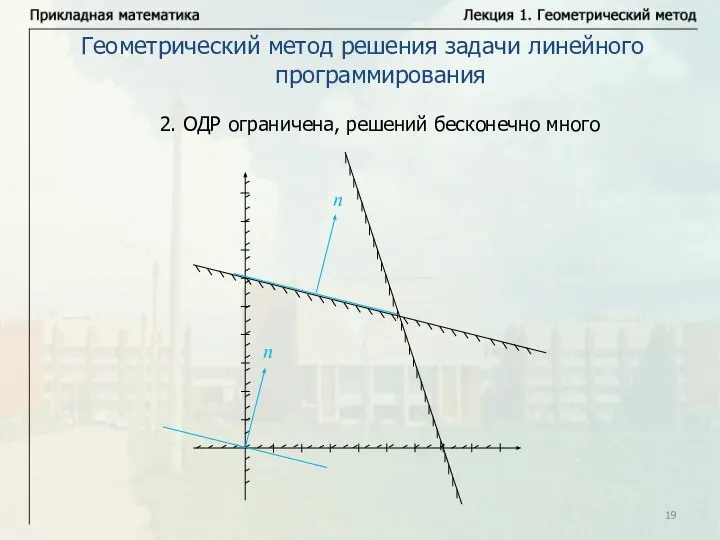
- 19. Геометрический метод решения задачи линейного программирования 2. ОДР ограничена, решений бесконечно много
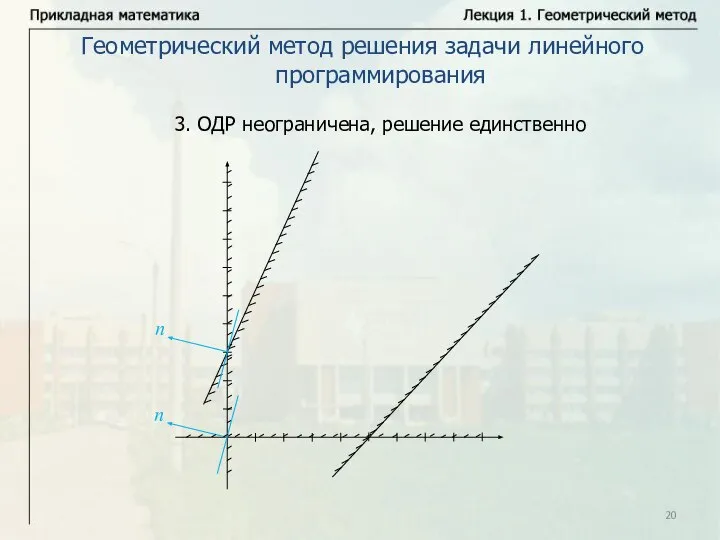
- 20. Геометрический метод решения задачи линейного программирования 3. ОДР неограничена, решение единственно
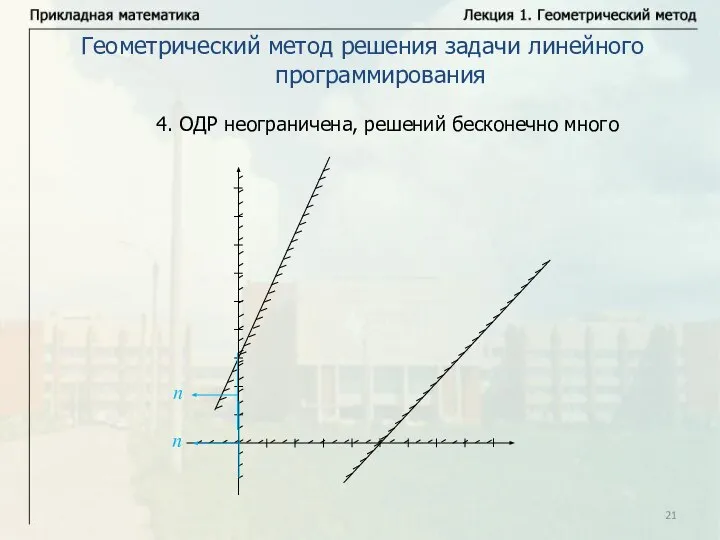
- 21. Геометрический метод решения задачи линейного программирования 4. ОДР неограничена, решений бесконечно много
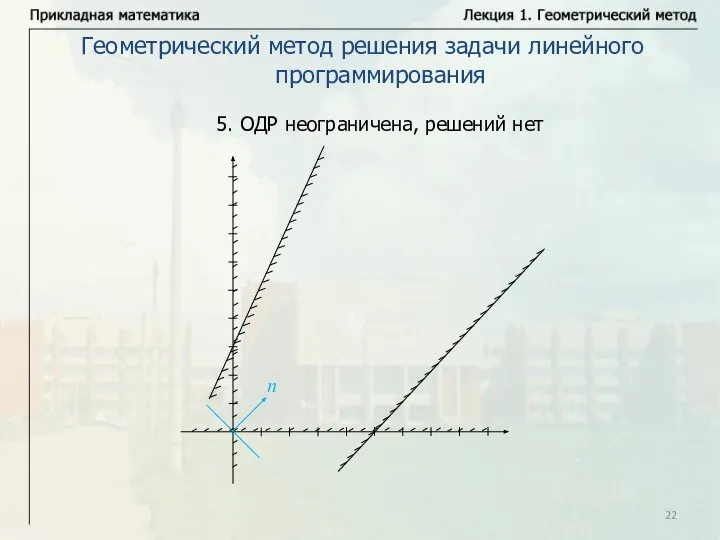
- 22. Геометрический метод решения задачи линейного программирования 5. ОДР неограничена, решений нет
- 23. Геометрический метод решения задачи линейного программирования 6. ОДР пуста, решений нет
- 24. Задания для самоконтроля 1. Какие из следующих функция являются линейными? 1) 2) 3) 4)
- 25. Задания для самоконтроля 2. Область допустимых решений – это 1) множество всех наборов значений переменных целевой
- 26. Задания для самоконтроля 3. Найдите значение целевой функции в задаче линейного программирования. 1) 763, 2) 835,
- 28. Скачать презентацию



















 Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Сложение отрицательных чисел
Сложение отрицательных чисел Презентация на тему Разность и её значение (1 класс)
Презентация на тему Разность и её значение (1 класс)  Весёлая математика: Давайте посчитаем
Весёлая математика: Давайте посчитаем Презентация на тему Комплексные числа 11 класс
Презентация на тему Комплексные числа 11 класс  Первообразная и интеграл
Первообразная и интеграл Основы математической статистики
Основы математической статистики Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций
Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций Многогранники в природе
Многогранники в природе теория вероятностей задачи
теория вероятностей задачи Задача по математике (4 класс, задание 85.1)
Задача по математике (4 класс, задание 85.1) Вычисление вероятностей сложных событий
Вычисление вероятностей сложных событий Ряды распределения в статистике
Ряды распределения в статистике Л 5 Функция одной переменной
Л 5 Функция одной переменной Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Исследование функции с помощью производной
Исследование функции с помощью производной Свойство параллелограмма
Свойство параллелограмма ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи Презентация на тему Тетраэдр (10 класс)
Презентация на тему Тетраэдр (10 класс)  Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  ЕГЭ 2012
ЕГЭ 2012 Многоугольники в нашей жизни
Многоугольники в нашей жизни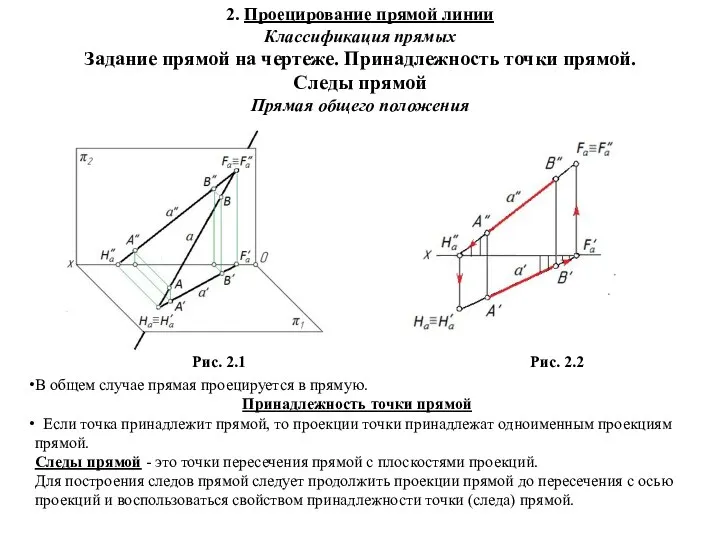 Начертательная геометрия. Проецирование прямой линии
Начертательная геометрия. Проецирование прямой линии Контрольная работа. 8 класс
Контрольная работа. 8 класс Множества натуральных чисел
Множества натуральных чисел Первый признак параллельности прямых
Первый признак параллельности прямых