Содержание
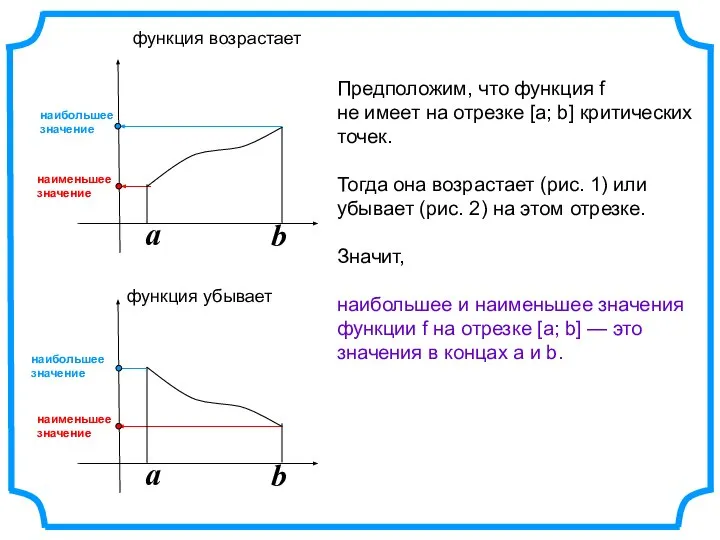
- 2. a b a b Предположим, что функция f не имеет на отрезке [а; b] критических точек.
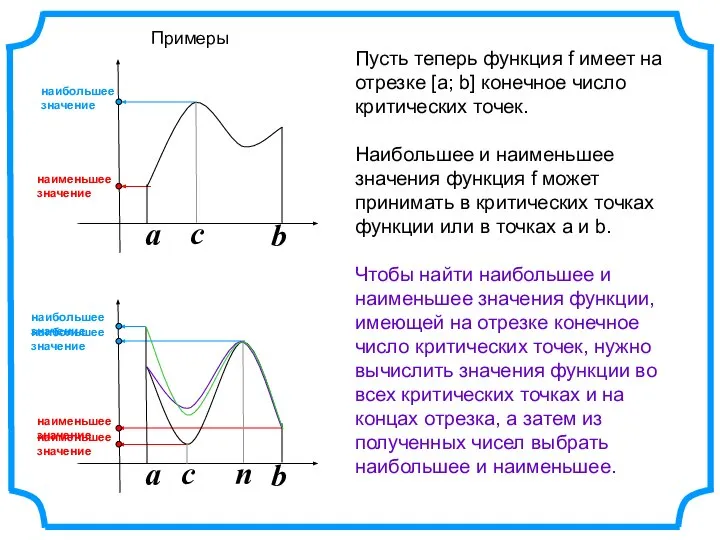
- 3. a b a b Пусть теперь функция f имеет на отрезке [а; b] конечное число критических
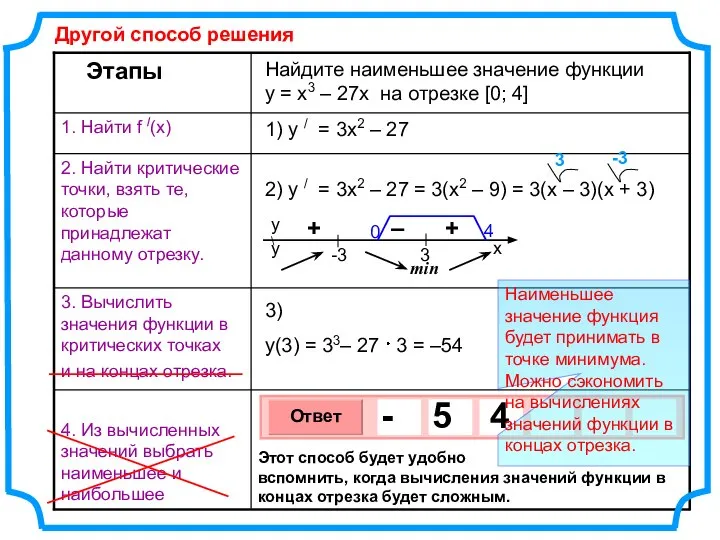
- 5. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1. Найдем критические
- 6. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
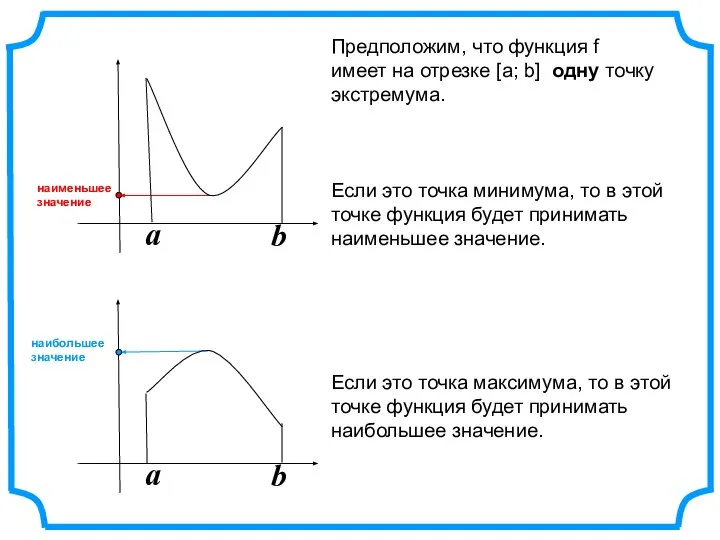
- 7. a b a b Предположим, что функция f имеет на отрезке [а; b] одну точку экстремума.
- 8. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 9. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1. Найдем критические
- 10. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наибольшее из полученных значений. 1) y(0) = 4
- 11. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наименьшее из полученных значений. 1) y(1) = 1
- 12. Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем критические точки, которые принадлежат
- 13. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем критические точки, которые принадлежат
- 14. Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем критические точки, которые принадлежат
- 15. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 16. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 17. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем критические точки, которые принадлежат
- 18. Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем критические точки, которые принадлежат
- 19. Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем критические точки, которые принадлежат
- 20. Найдите наибольшее значение функции y = ln(x+5)5 – 5x на отрезке [-4,5; 0] 11. max Наибольшее
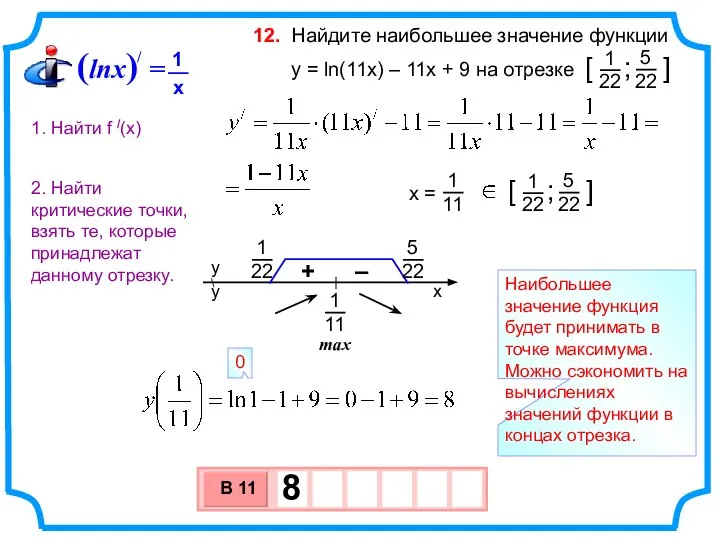
- 21. Найдите наибольшее значение функции y = ln(11x) – 11x + 9 на отрезке 12. max Наибольшее
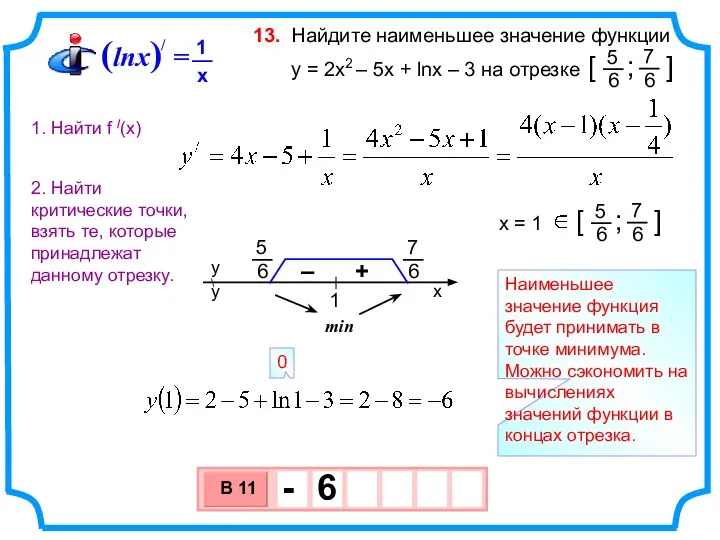
- 22. Найдите наименьшее значение функции y = 2х2 – 5x + lnx – 3 на отрезке 13.
- 23. Найдите наибольшее значение функции y = 7cosx +16x – 2 на отрезке 14. Функция на всей
- 24. Критических точек нет. Тогда наибольшее значение функция будет принимать в одном из концов отрезка. Можно было
- 25. Функция на всей области определения убывает. Нетрудно догадаться, что у / Тогда наименьшее значение функция будет
- 26. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
- 27. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
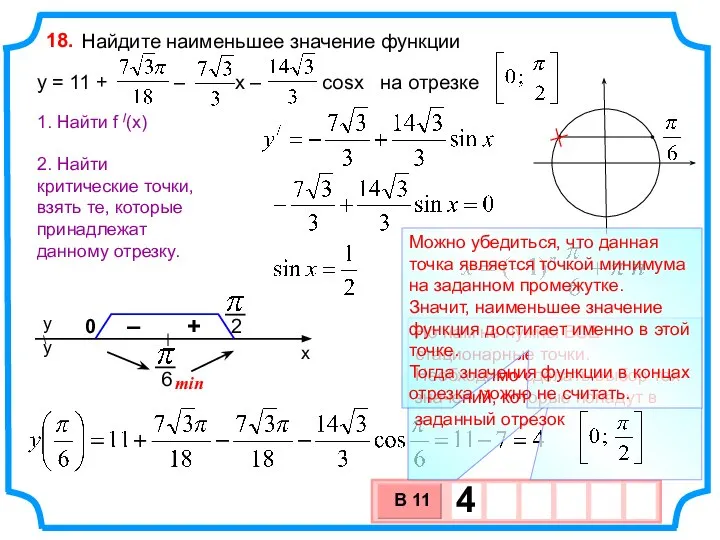
- 28. Найдите наименьшее значение функции y = 11 + – х – cosx на отрезке 18. 1.
- 29. Найдите наименьшее значение функции y = 4tgx – 4x – 4 + 5 на отрезке 19.
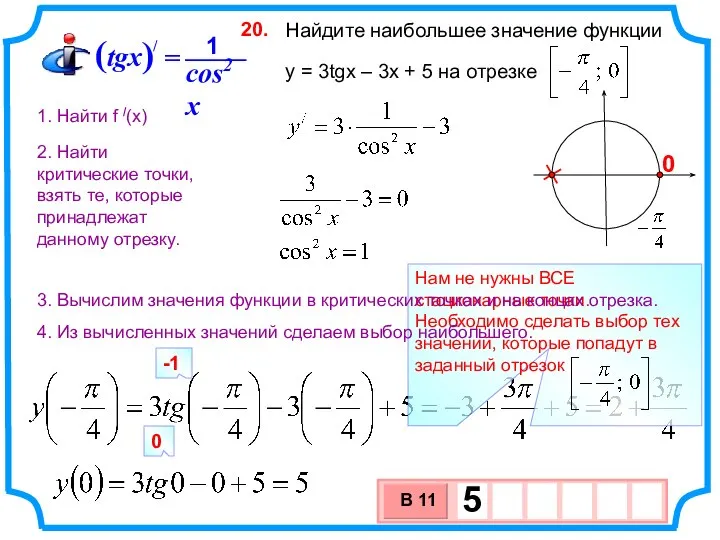
- 30. Найдите наибольшее значение функции y = 3tgx – 3x + 5 на отрезке 20. 1. Найти
- 32. Скачать презентацию






![Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-11.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-12.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-13.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-14.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-15.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-16.jpg)
![Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-17.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1046755/slide-18.jpg)







 Многоугольники в нашей жизни
Многоугольники в нашей жизни Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс XII командный турнир по математике Математические бои
XII командный турнир по математике Математические бои Пирамида. Элементы пирамиды. Поверхность пирамиды
Пирамида. Элементы пирамиды. Поверхность пирамиды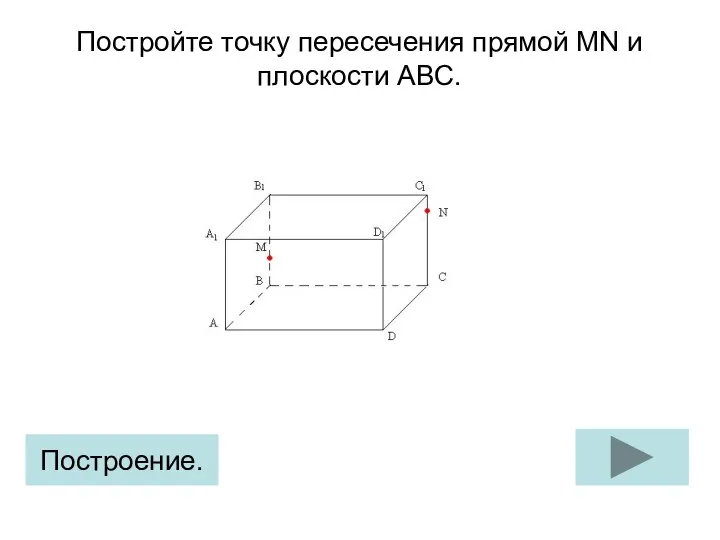 Точка пересечения прямой MN и плоскости ABC. Построение (задание 2)
Точка пересечения прямой MN и плоскости ABC. Построение (задание 2) Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс
Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс Переводчицы. Задача
Переводчицы. Задача Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Вычисления вида 32 + 8, 40 – 8
Вычисления вида 32 + 8, 40 – 8 Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11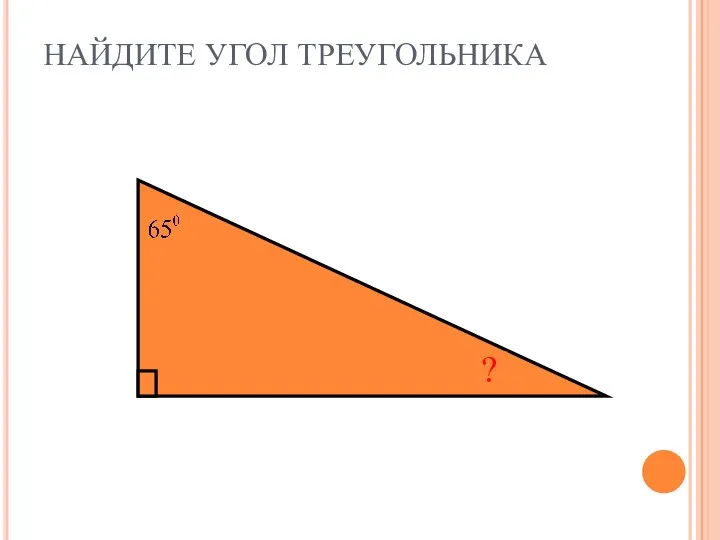 Нахождение угла треугольника
Нахождение угла треугольника Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Окружность и круг
Окружность и круг Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Математика и Незнайка. Математическая сказка
Математика и Незнайка. Математическая сказка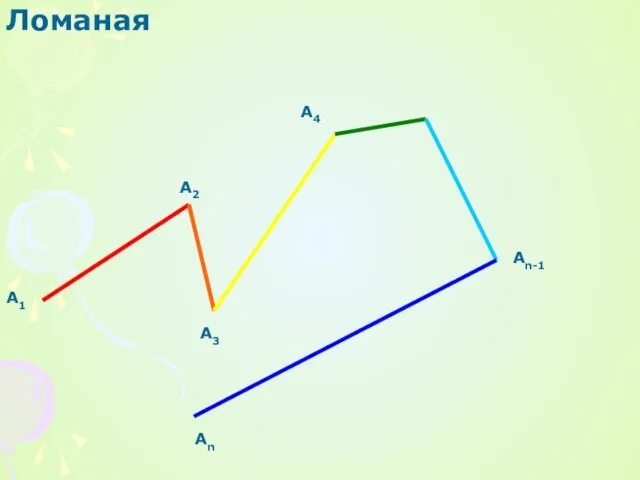 Презентация на тему Ломаная
Презентация на тему Ломаная  Основы геометрии
Основы геометрии История дифференциального исчисления
История дифференциального исчисления Построение графиков функций
Построение графиков функций Цифра в 21 веке
Цифра в 21 веке Карточки по математике
Карточки по математике Окружность и длина окружности
Окружность и длина окружности Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Методы решения логарифмических уравнений. 11 класс
Методы решения логарифмических уравнений. 11 класс Площадь параллелограмма и ромба
Площадь параллелограмма и ромба