- Главная
- Математика
- Решение задач. Куб, параллелепипед, призма

Содержание
Слайд 216. Вариант 116 http://alexlarin.net/ege/2015/trvar116.pdf
В прямоугольном параллелепипеде ABCDА1В1С1D1 АВ = ВС = 8,
16. Вариант 116 http://alexlarin.net/ege/2015/trvar116.pdf
В прямоугольном параллелепипеде ABCDА1В1С1D1 АВ = ВС = 8,
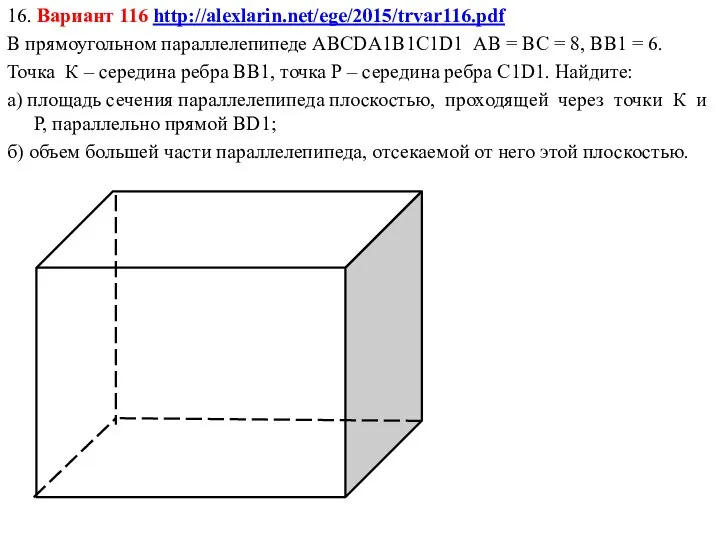
ВВ1 = 6.
Точка К – середина ребра ВВ1, точка Р – середина ребра С1D1. Найдите:
а) площадь сечения параллелепипеда плоскостью, проходящей через точки К и Р, параллельно прямой ВD1;
б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью.
Точка К – середина ребра ВВ1, точка Р – середина ребра С1D1. Найдите:
а) площадь сечения параллелепипеда плоскостью, проходящей через точки К и Р, параллельно прямой ВD1;
б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью.
Слайд 3 16. В кубе ABCDA1B1C1D1 все ребра равны 5. На его ребре
16. В кубе ABCDA1B1C1D1 все ребра равны 5. На его ребре
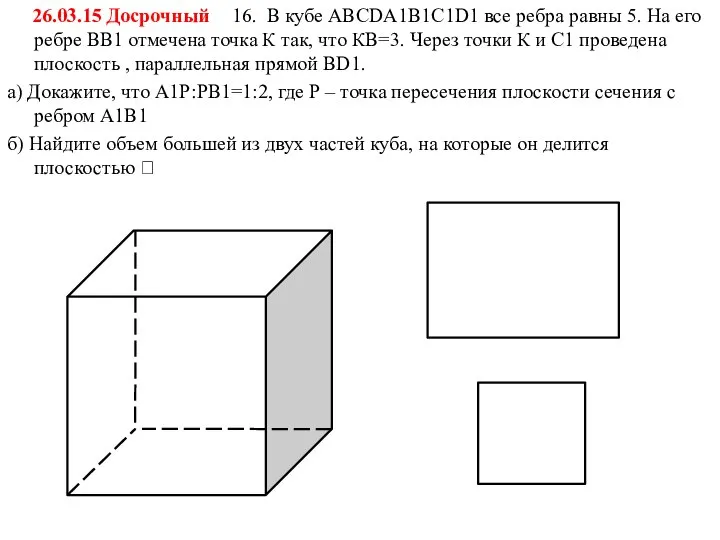
ВВ1 отмечена точка К так, что КВ=3. Через точки К и С1 проведена плоскость , параллельная прямой ВD1.
а) Докажите, что А1Р:РВ1=1:2, где Р – точка пересечения плоскости сечения с ребром А1В1
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью
а) Докажите, что А1Р:РВ1=1:2, где Р – точка пересечения плоскости сечения с ребром А1В1
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью
26.03.15 Досрочный
 Линейное уравнение с одной переменной. Подготовка к контрольной работе
Линейное уравнение с одной переменной. Подготовка к контрольной работе Комбинаторика. Комбинаторные объекты
Комбинаторика. Комбинаторные объекты Случайные величины
Случайные величины Сравни выражения
Сравни выражения Таблица для мешка по двум признакам
Таблица для мешка по двум признакам Деление. Неправильные дроби
Деление. Неправильные дроби Действия с натуральными числами. Решение задач, с помощью уравнений
Действия с натуральными числами. Решение задач, с помощью уравнений Треугольник. Периметр треугольника. 9 класс
Треугольник. Периметр треугольника. 9 класс Интегрированный урок на закрепление знаний по математике, биологии с применением информационных технологий. Можно создавать тес
Интегрированный урок на закрепление знаний по математике, биологии с применением информационных технологий. Можно создавать тес Презентация на тему Конкретный смысл действия умножения (2 класс)
Презентация на тему Конкретный смысл действия умножения (2 класс)  Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы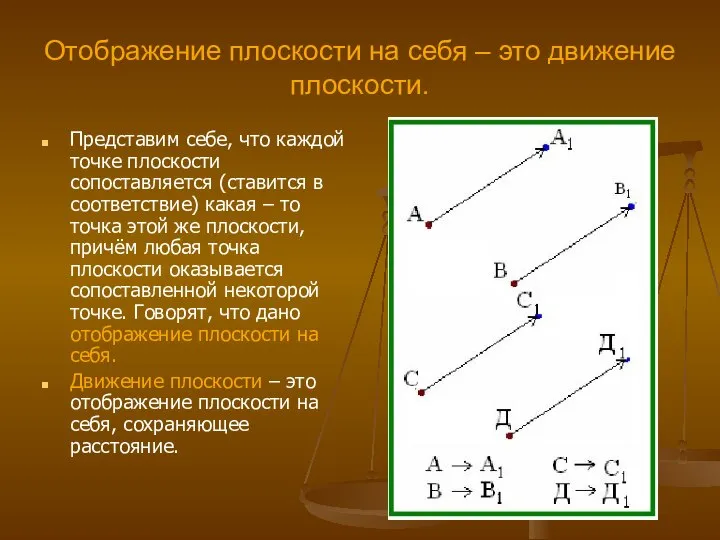 Геометрические преобразования плоскости
Геометрические преобразования плоскости Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Математические методы анализа динамики цен на нефтегазовых рынках в работах американских экономистов
Математические методы анализа динамики цен на нефтегазовых рынках в работах американских экономистов Решение уравнений
Решение уравнений Випадкова подія. Відносна частота події. Імовірність події
Випадкова подія. Відносна частота події. Імовірність події Обратные тригонометрические функции
Обратные тригонометрические функции Платоновы и Архимедовы тела
Платоновы и Архимедовы тела Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Великолепная пятерка. Игра
Великолепная пятерка. Игра Задачи на построение примера. Геометрические конструкции
Задачи на построение примера. Геометрические конструкции Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Окружность и прямая
Окружность и прямая Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Сумма углов треугольника
Сумма углов треугольника Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? КВН по математике Привет друзья! Сегодня в школе Большой и интересный день Мы приготовили веселый Наш школьный праздник КВН.
КВН по математике Привет друзья! Сегодня в школе Большой и интересный день Мы приготовили веселый Наш школьный праздник КВН. Презентация на тему Описательная статистика
Презентация на тему Описательная статистика