Содержание
- 2. Замечание!!! Определение перпендикуляра к прямой (описательное) изучаем из пункта 16; теорему о проведении перпендикуляра к прямой
- 3. Замечание!!! На след слайде изучим как можно построить перпендикуляр из точки к прямой!!!
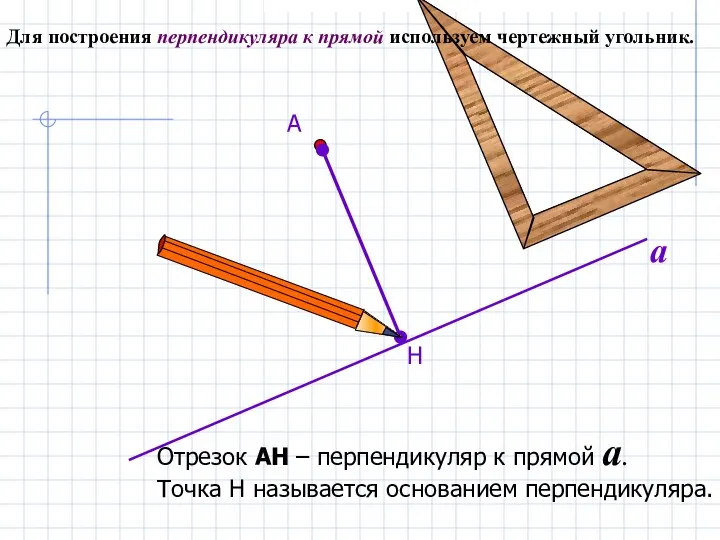
- 4. Для построения перпендикуляра к прямой используем чертежный угольник. Н А Отрезок АН – перпендикуляр к прямой
- 5. Замечание!!! На след слайде подводим мышку на слова медиана, высота, биссектриса и изучаем эти понятия
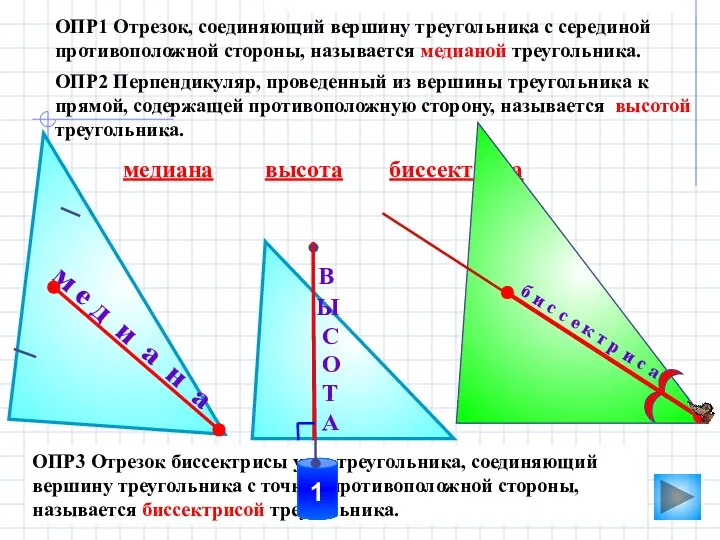
- 6. м е д и а н а ОПР3 Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
- 7. Замечание!!! На след слайде еще раз на примере устной задачи отрабатываем понятия медиана, высота, биссектриса
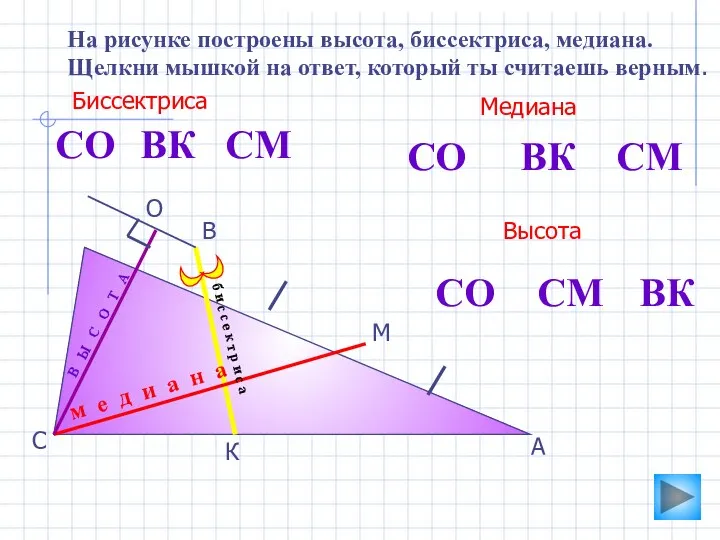
- 8. О А В С К М На рисунке построены высота, биссектриса, медиана. Щелкни мышкой на ответ,
- 9. Замечание!!! На след слайдах изучаем свойство медиан треугольника; свойство высот треугольника (остроугольного, прямоугольного и тупоугольного)
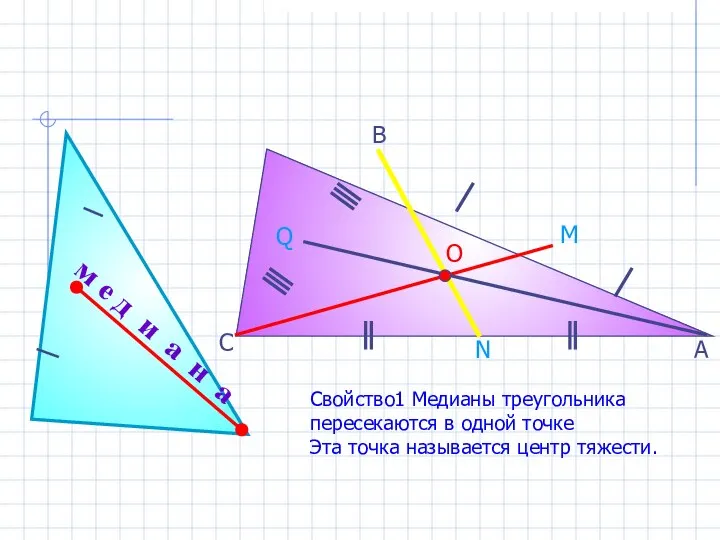
- 10. м е д и а н а В С М А N Q Свойство1 Медианы треугольника
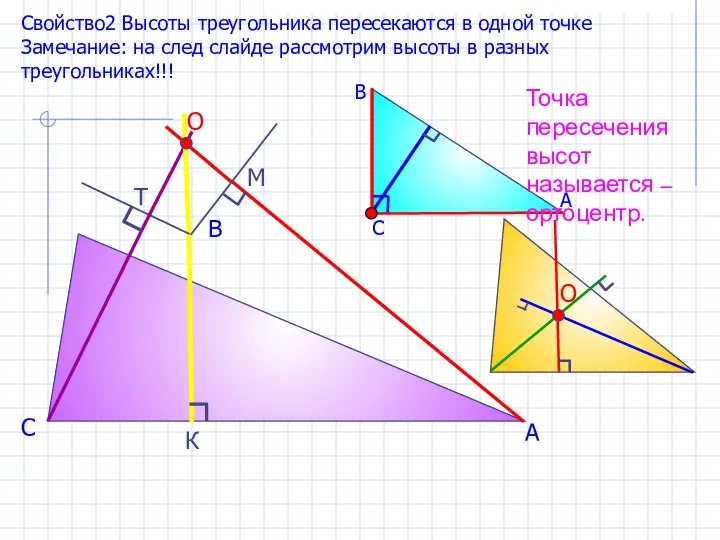
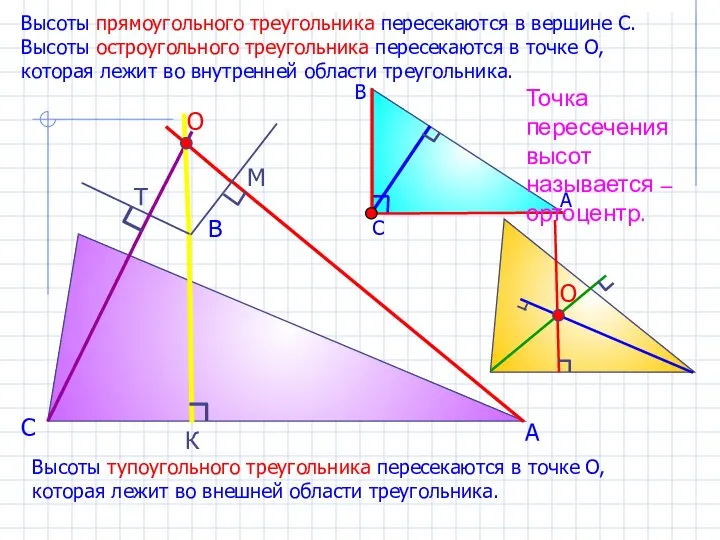
- 11. А В С К М Т Свойство2 Высоты треугольника пересекаются в одной точке Замечание: на след
- 12. А В С К М Т Высоты тупоугольного треугольника пересекаются в точке О, которая лежит во
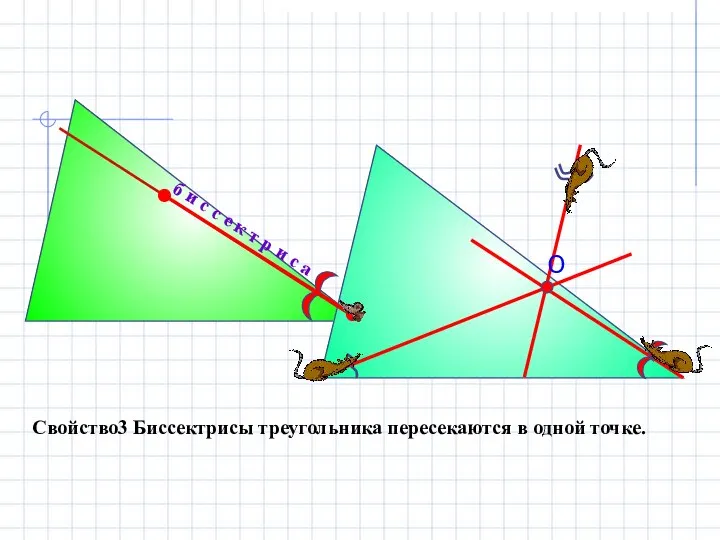
- 13. Свойство3 Биссектрисы треугольника пересекаются в одной точке. б и с с е к т р и
- 14. Замечание!!! На след слайдах изучаем понятия равнобедренного и равностороннего треугольника в рисунках, а из пункта 18
- 16. Скачать презентацию






 Округление.десятичных дробей
Округление.десятичных дробей Теория вероятностей. Задачи ЕГЭ
Теория вероятностей. Задачи ЕГЭ Действия с десятичными дробями
Действия с десятичными дробями Согласование существительных с числительными
Согласование существительных с числительными Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -
Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -  Задание 19. Профиль
Задание 19. Профиль Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма 2_Teoria_veroyatnostey_920_is
2_Teoria_veroyatnostey_920_is Усеченная пирамида
Усеченная пирамида Взаимосвязь между скоростью, временем и расстоянием. Умножение на числа, оканчивающиеся нулями
Взаимосвязь между скоростью, временем и расстоянием. Умножение на числа, оканчивающиеся нулями Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат
Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат Пропозиційна логика (продовження). Лекція №2
Пропозиційна логика (продовження). Лекція №2 Задачи с дробями
Задачи с дробями Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника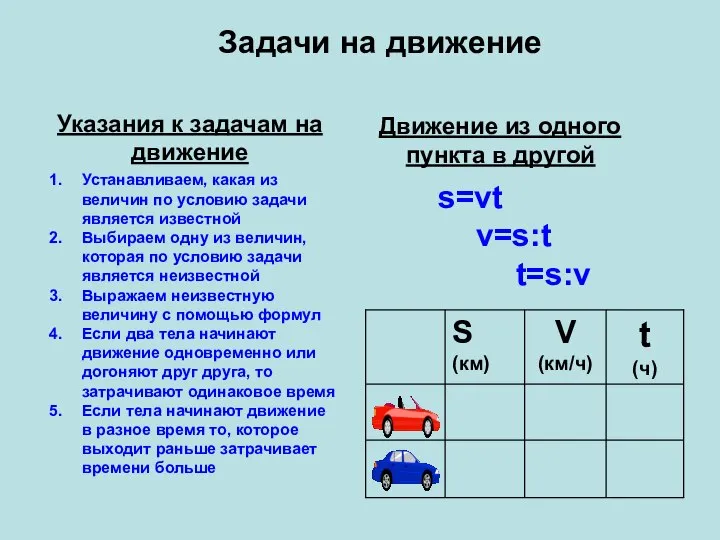 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Понятие вектора
Понятие вектора Понятие вектора в пространстве
Понятие вектора в пространстве Применение распределительного свойства умножения
Применение распределительного свойства умножения Запомни цифры
Запомни цифры Презентация на тему Квадратичная функция
Презентация на тему Квадратичная функция  Уравнение окружности
Уравнение окружности Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Взаимное расположение прямых в пространстве. Угол между двумя прямыми
Взаимное расположение прямых в пространстве. Угол между двумя прямыми Aproximarea numerică a funcţiilor. Metode numerice – curs 10
Aproximarea numerică a funcţiilor. Metode numerice – curs 10 Сумма углов треугольника
Сумма углов треугольника Число или цифра 5
Число или цифра 5 Признаки параллельности прямых
Признаки параллельности прямых Задача з піцою
Задача з піцою