Содержание
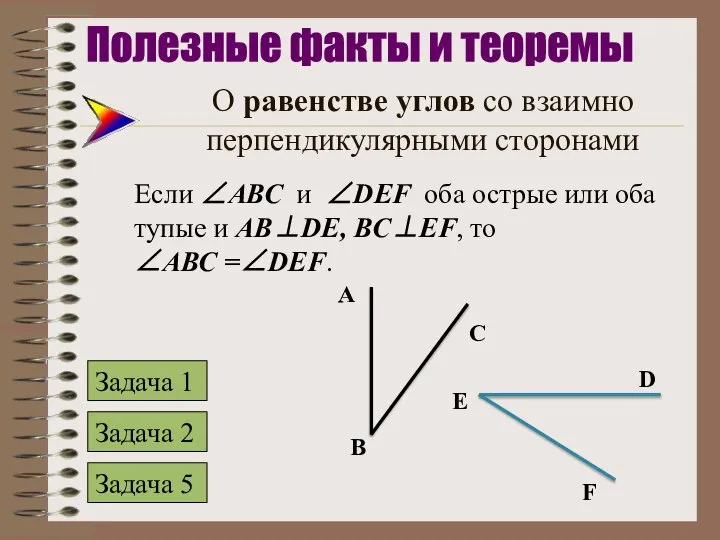
- 2. О равенстве углов со взаимно перпендикулярными сторонами Если ∠АВС и ∠DEF оба острые или оба тупые
- 3. О точках пересечения медиан, биссектрис, высот треугольника Три биссектрисы треугольника пересекаются в одной точке. Три высоты
- 4. Свойства средней линии трапеции Средняя линия параллельна основаниям трапеции. Средняя линия (и только она) делит пополам
- 5. Свойство медианы в прямоугольном треугольнике В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. Если
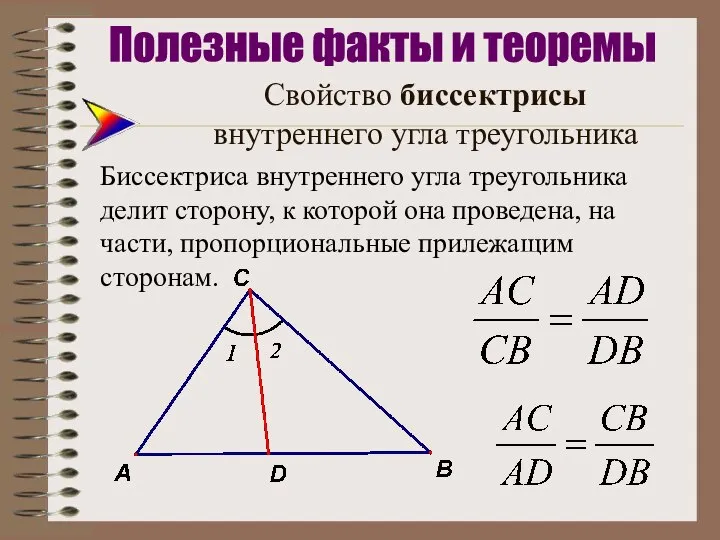
- 6. Свойство биссектрисы внутреннего угла треугольника Биссектриса внутреннего угла треугольника делит сторону, к которой она проведена, на
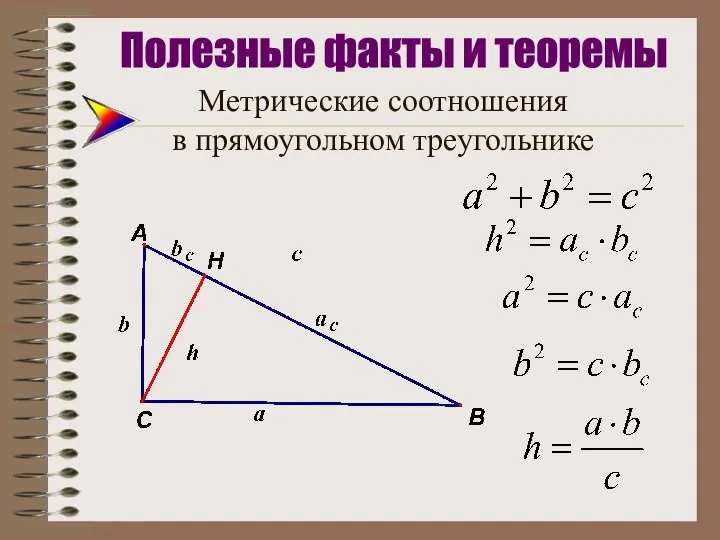
- 7. Метрические соотношения в прямоугольном треугольнике Полезные факты и теоремы
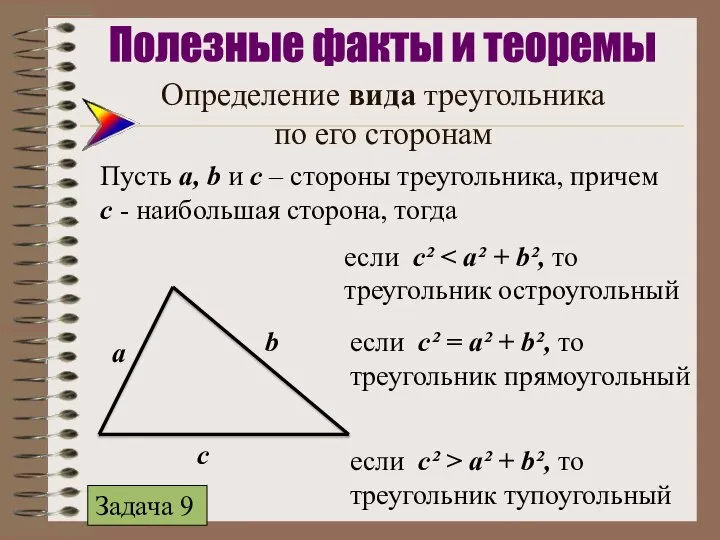
- 8. Определение вида треугольника по его сторонам Пусть а, b и с – стороны треугольника, причем с
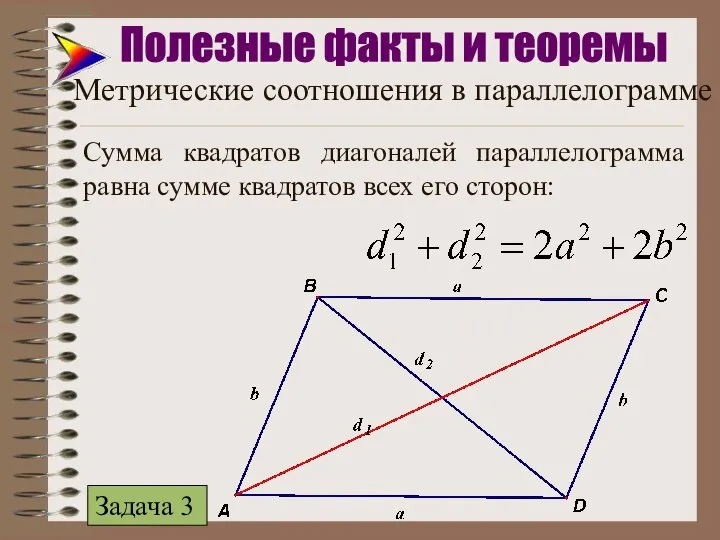
- 9. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: Полезные факты и теоремы Метрические соотношения
- 10. Если два треугольника подобны, то любой линейный элемент (или сумма линейных элементов) одного треугольника относится к
- 11. Рассмотреть эти отрезки как стороны двух треугольников и доказать, что треугольники равны. Заменить отрезок а равным
- 12. Проведение прямой, параллельной или перпендикулярной одной из имеющихся. Проведение вспомогательной биссектрисы. Дополнительные построения Удвоение медианы треугольника
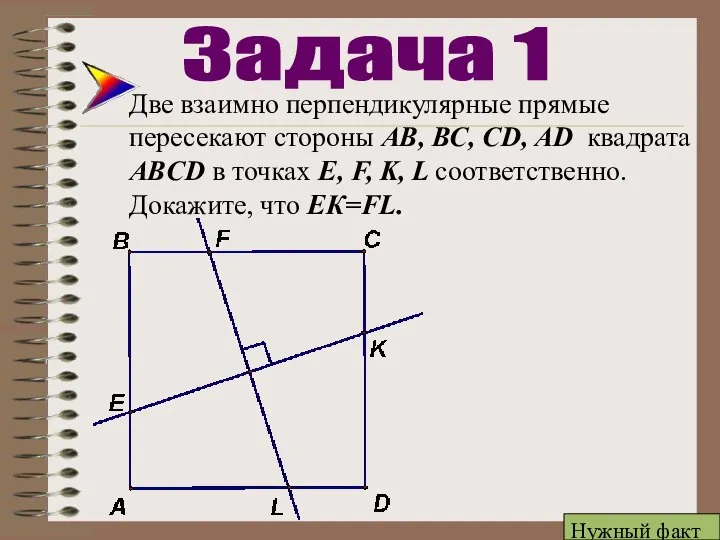
- 13. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
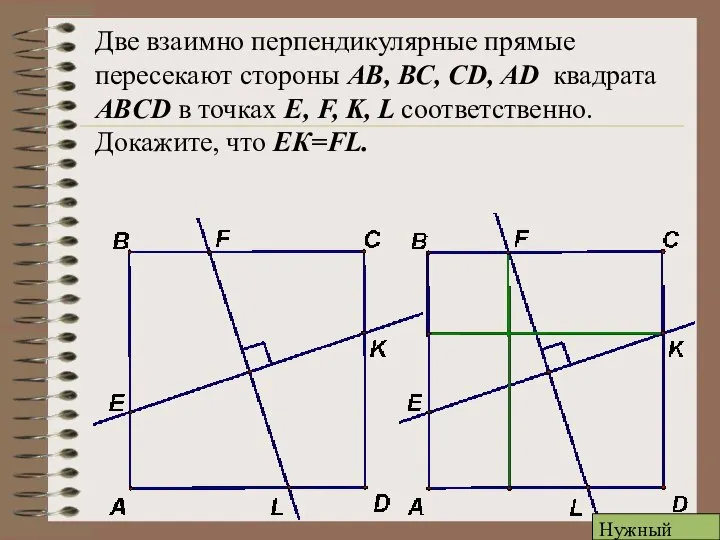
- 14. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
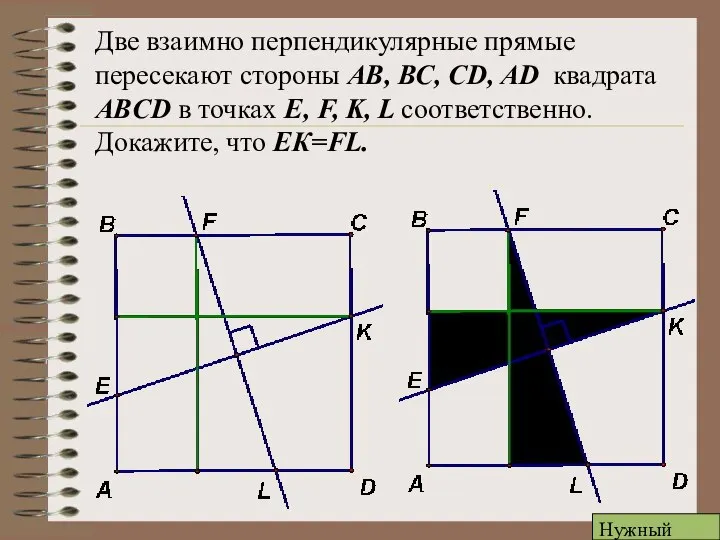
- 15. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
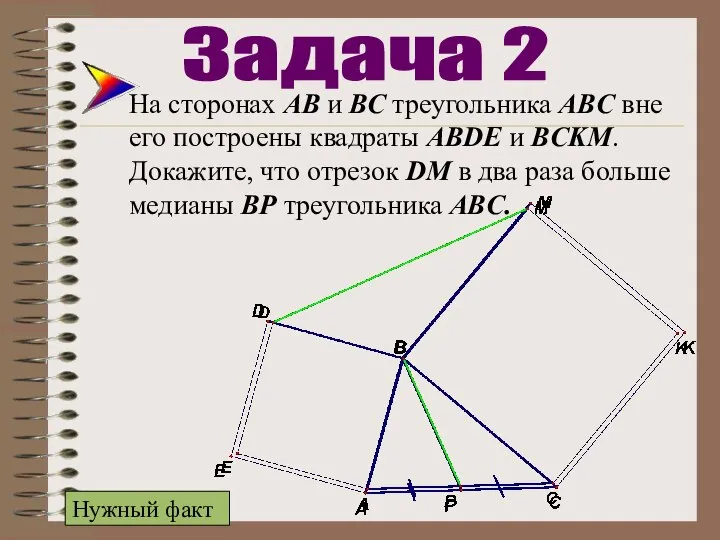
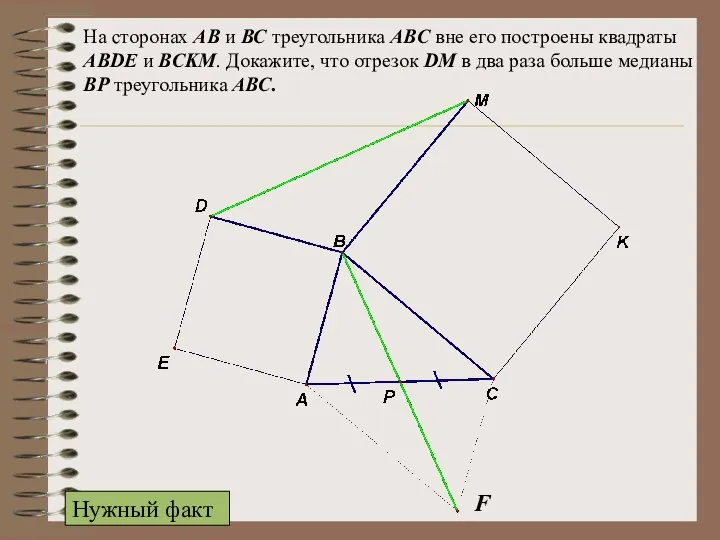
- 16. На сторонах АВ и ВС треугольника ABC вне его построены квадраты ABDE и BCKM. Докажите, что
- 17. На сторонах АВ и ВС треугольника ABC вне его построены квадраты ABDE и BCKM. Докажите, что
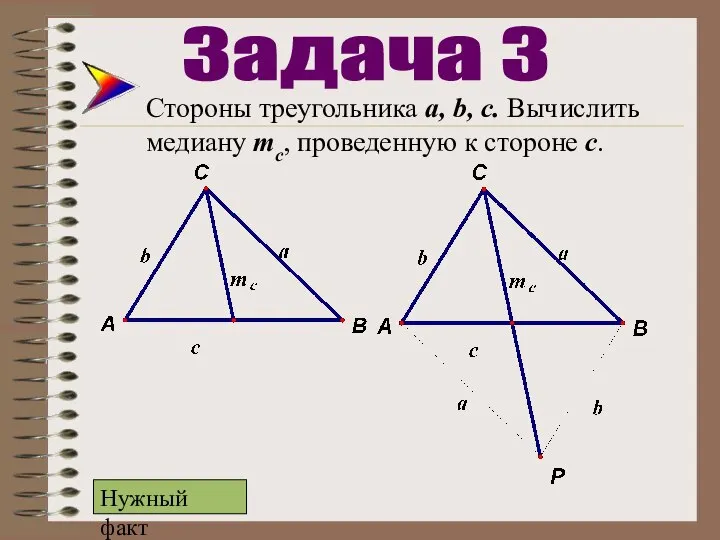
- 18. Стороны треугольника а, b, c. Вычислить медиану mc, проведенную к стороне с. Задача 3 Нужный факт
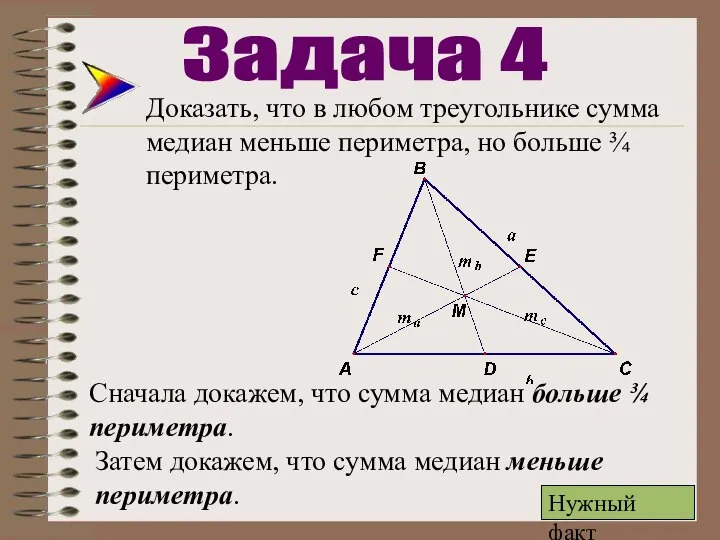
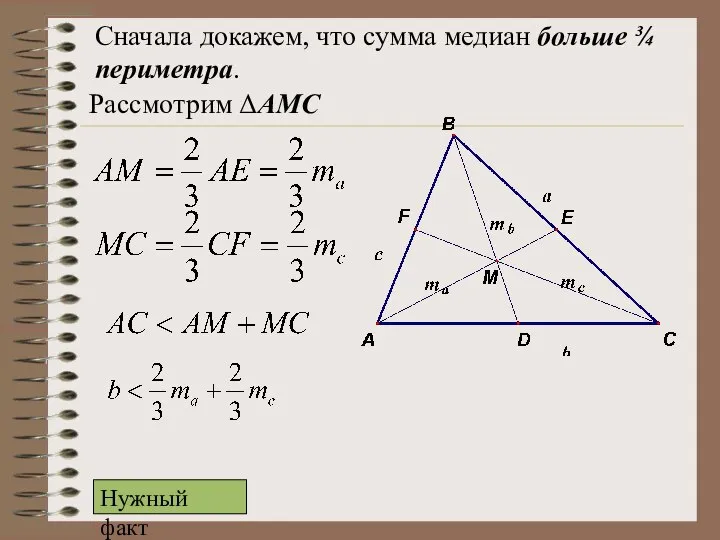
- 19. Доказать, что в любом треугольнике сумма медиан меньше периметра, но больше ¾ периметра. Задача 4 Сначала
- 20. Сначала докажем, что сумма медиан больше ¾ периметра. Рассмотрим ΔАМС Нужный факт
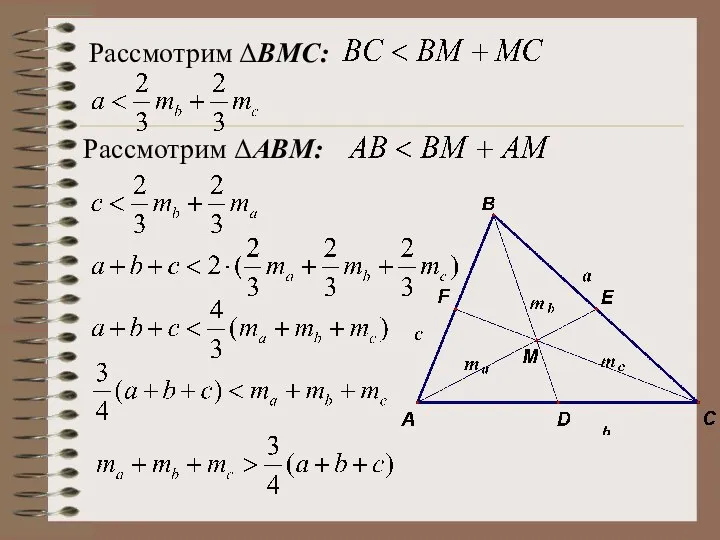
- 21. Рассмотрим ΔBМС: Рассмотрим ΔABМ:
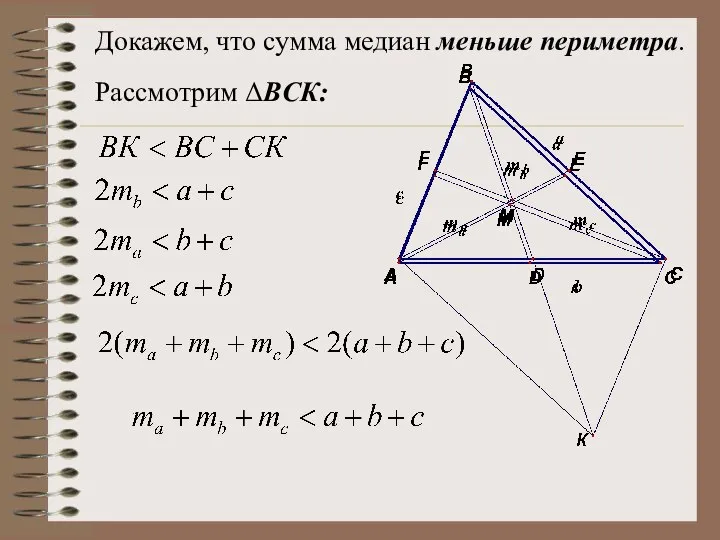
- 22. Докажем, что сумма медиан меньше периметра. Рассмотрим ΔBСК:
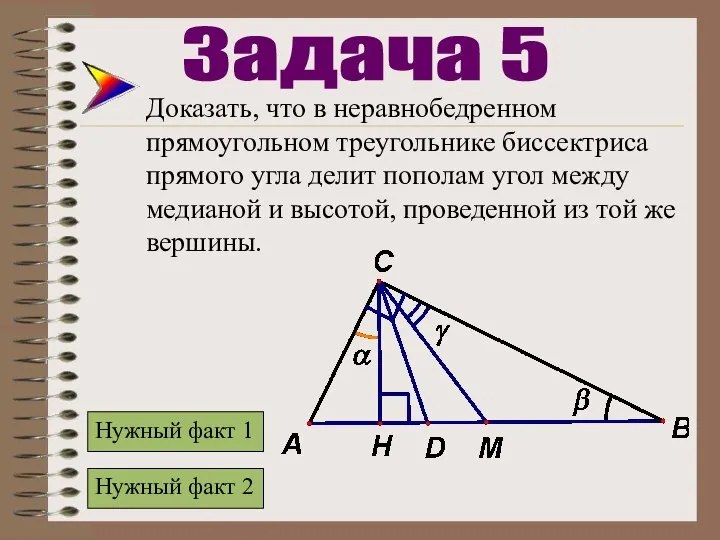
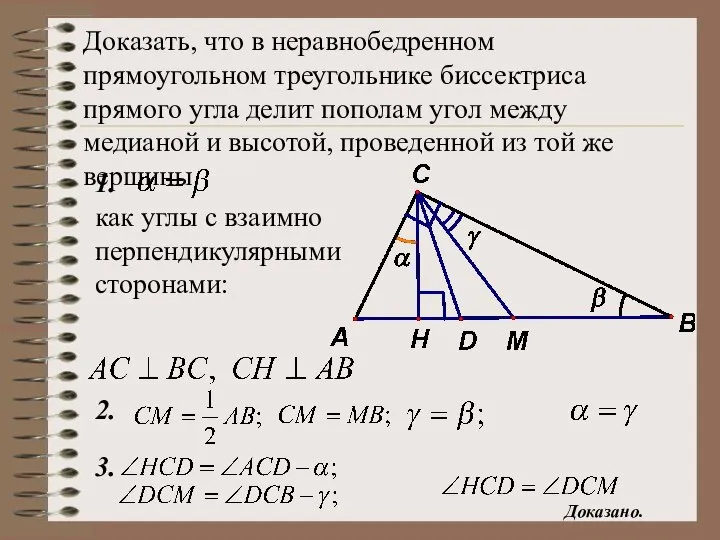
- 23. Доказать, что в неравнобедренном прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой,
- 24. Доказать, что в неравнобедренном прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой,
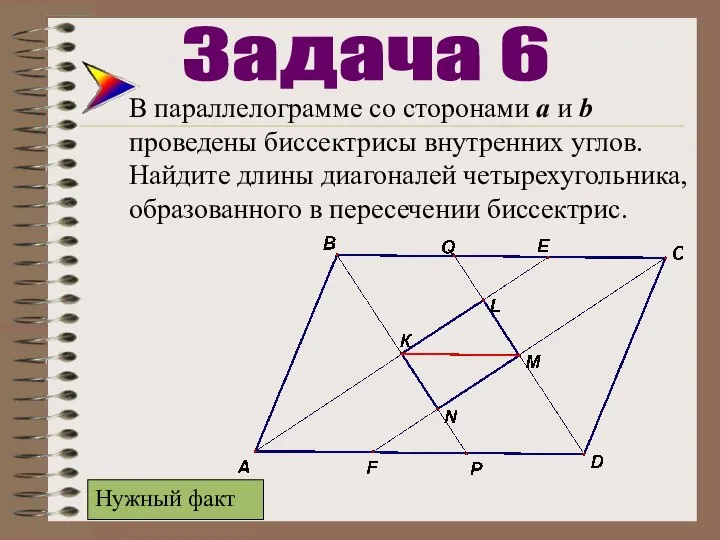
- 25. В параллелограмме со сторонами а и b проведены биссектрисы внутренних углов. Найдите длины диагоналей четырехугольника, образованного
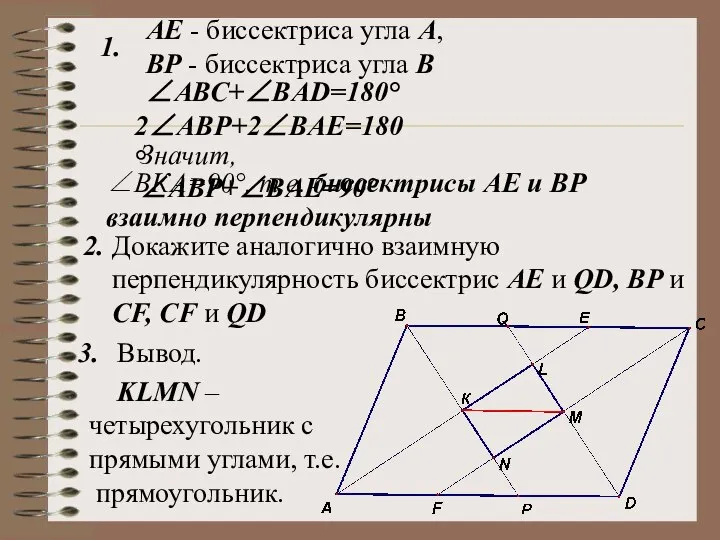
- 26. АЕ - биссектриса угла А, ВР - биссектриса угла В 1. 2. KLMN – четырехугольник с
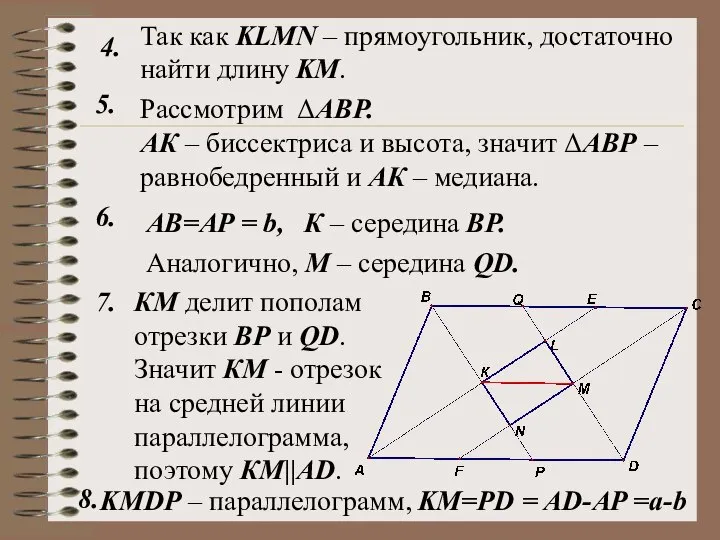
- 27. Рассмотрим ΔАВР. 4. 5. Так как KLMN – прямоугольник, достаточно найти длину KM. 7. KM=PD =
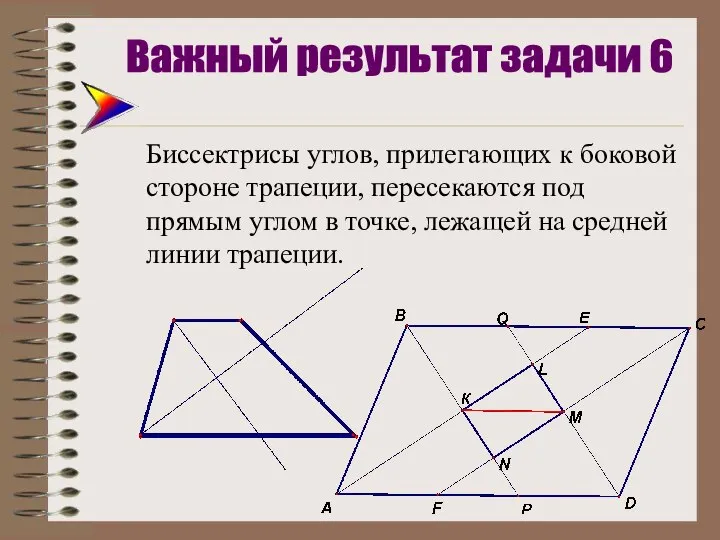
- 28. Биссектрисы углов, прилегающих к боковой стороне трапеции, пересекаются под прямым углом в точке, лежащей на средней
- 29. Основным методом составления уравнений в геометрических задачах является метод опорного элемента. Он заключается в том, что
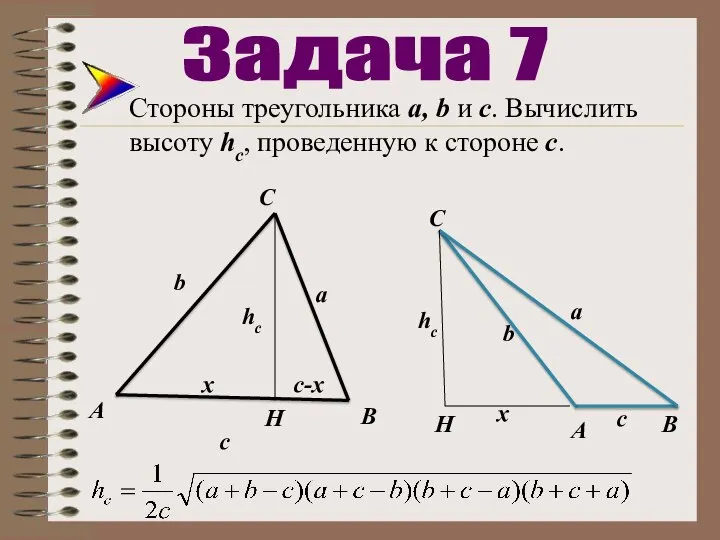
- 30. Стороны треугольника а, b и с. Вычислить высоту hc, проведенную к стороне с. Задача 7 x
- 31. Если в задаче требуется найти отношение каких-либо величин, то она решается методом введения вспомогательного параметра. В
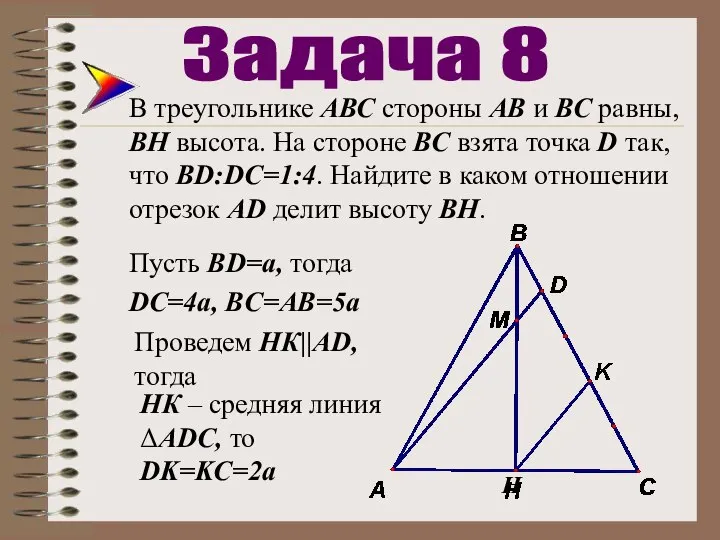
- 32. В треугольнике АВС стороны АВ и ВС равны, ВН высота. На стороне ВС взята точка D
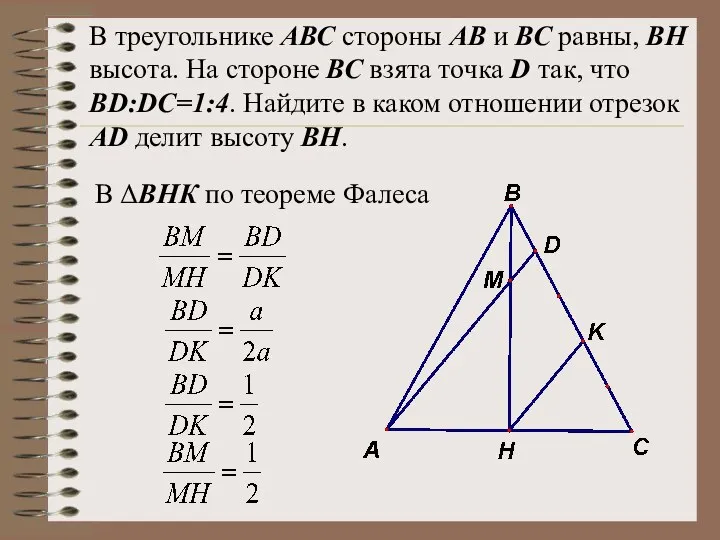
- 33. В треугольнике АВС стороны АВ и ВС равны, ВН высота. На стороне ВС взята точка D
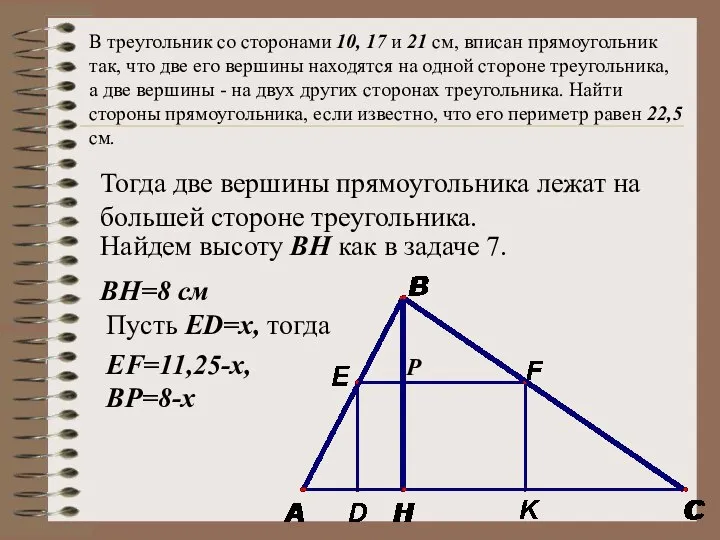
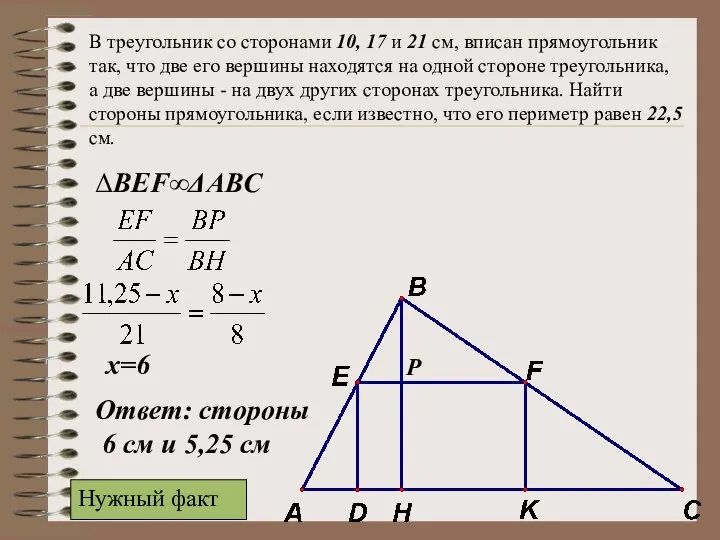
- 34. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
- 35. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
- 36. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
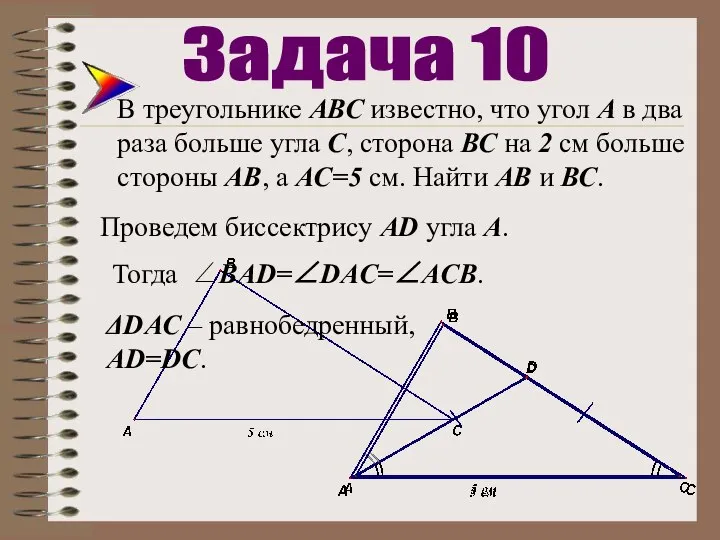
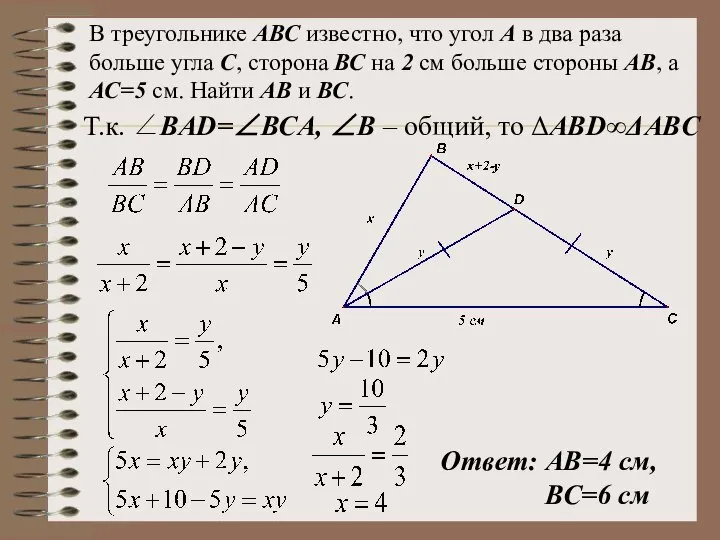
- 37. В треугольнике АВС известно, что угол А в два раза больше угла С, сторона ВС на
- 38. В треугольнике АВС известно, что угол А в два раза больше угла С, сторона ВС на
- 40. Скачать презентацию









 Подготовка к ЕГЭ. вычисление значений производной. В8
Подготовка к ЕГЭ. вычисление значений производной. В8 Случаи сложения вида +4
Случаи сложения вида +4 9_setyabrya_distant_urok_matem
9_setyabrya_distant_urok_matem Доказательство клауз. Лекция 7
Доказательство клауз. Лекция 7 Разгадайте загадки
Разгадайте загадки Решение треугольников
Решение треугольников Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Шар. Объём шара
Шар. Объём шара Нахождение неопределенного интеграла
Нахождение неопределенного интеграла Основные тригонометрические тождества
Основные тригонометрические тождества Неравенства. Обобщающий урок. Подготовка к ЕГЭ
Неравенства. Обобщающий урок. Подготовка к ЕГЭ Признак параллельности плоскостей
Признак параллельности плоскостей Таблица сложения
Таблица сложения Справочный материал. 9 класс
Справочный материал. 9 класс Графический диктант Кенгуру
Графический диктант Кенгуру Элементы комбинаторики
Элементы комбинаторики Математика 1 класс
Математика 1 класс Презентация 1
Презентация 1 Тройные и многократные интегралы
Тройные и многократные интегралы Презентация на тему Разложение многочленов на множители
Презентация на тему Разложение многочленов на множители  Презентация на тему Письменное умножение на двузначное число (4 класс)
Презентация на тему Письменное умножение на двузначное число (4 класс)  Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Теория вероятностей
Теория вероятностей Решение задач
Решение задач Додавання, редагування та формування таблиць
Додавання, редагування та формування таблиць Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Системы уравнений. Способы решения систем уравнений
Системы уравнений. Способы решения систем уравнений Занимательная математика
Занимательная математика