Содержание
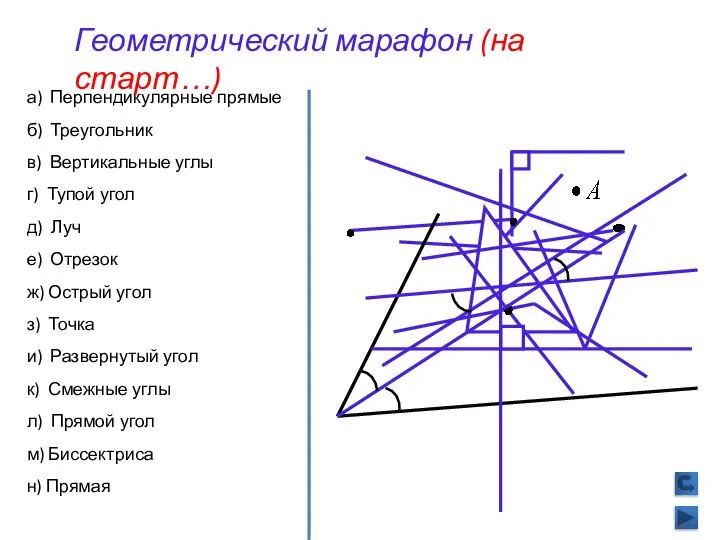
- 2. а) Перпендикулярные прямые б) Треугольник в) Вертикальные углы г) Тупой угол д) Луч е) Отрезок ж)
- 3. Проверь себя: е , з , к , л , д , г , и ,
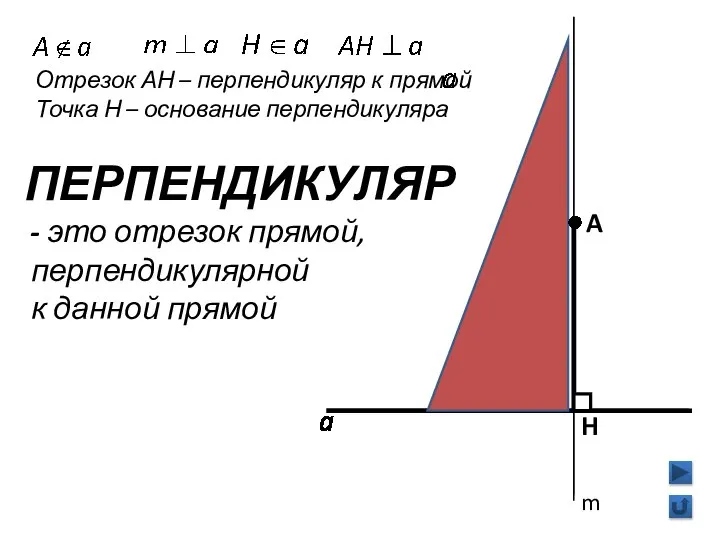
- 4. A H ПЕРПЕНДИКУЛЯР - это отрезок прямой, перпендикулярной к данной прямой Отрезок АН – перпендикуляр к
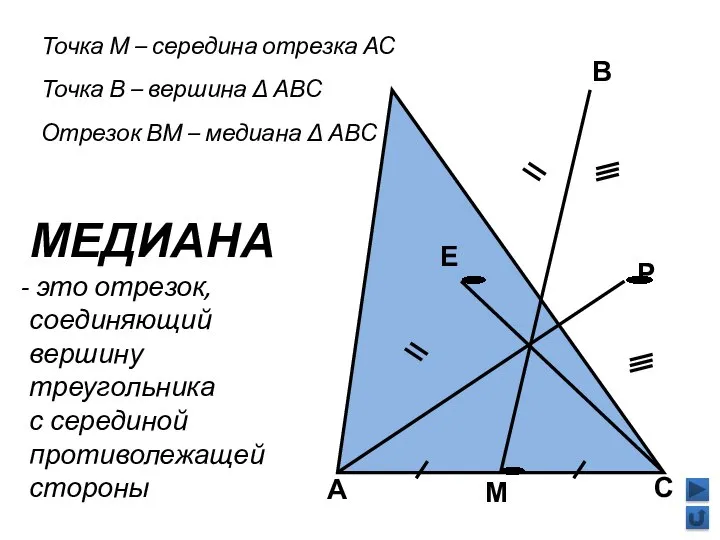
- 5. А В М С Точка М – середина отрезка АС Точка В – вершина Δ АВС
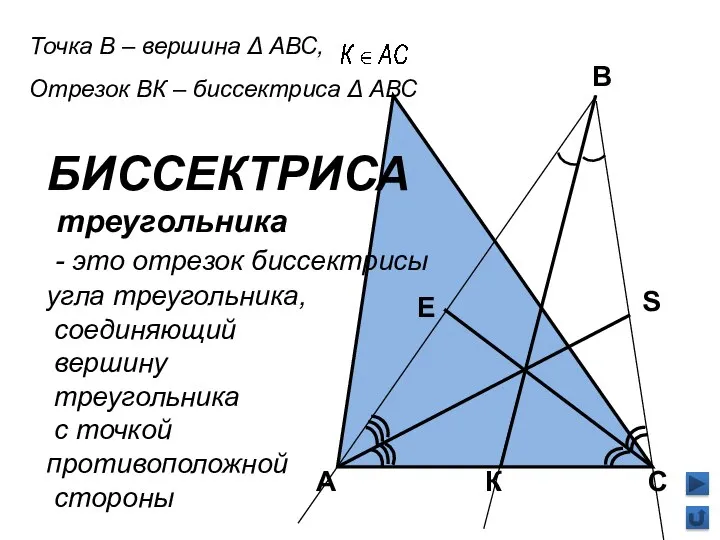
- 6. В А С К Точка В – вершина Δ АВС, Отрезок ВК – биссектриса Δ АВС
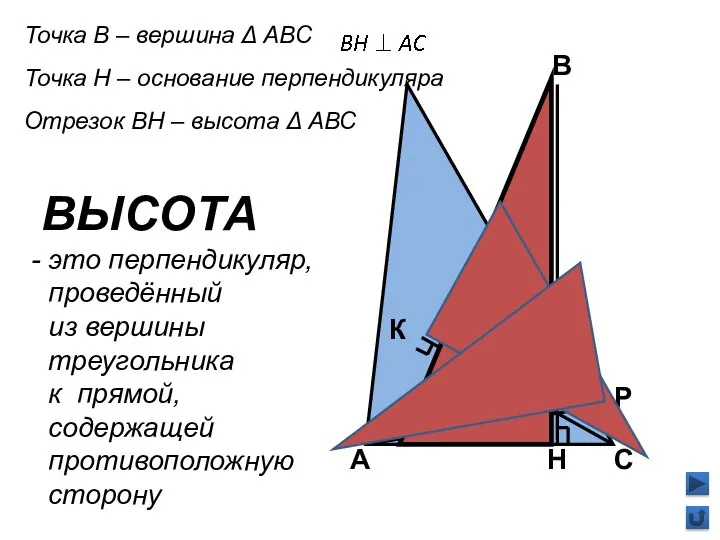
- 7. А Н С В Точка В – вершина Δ АВС Точка Н – основание перпендикуляра Отрезок
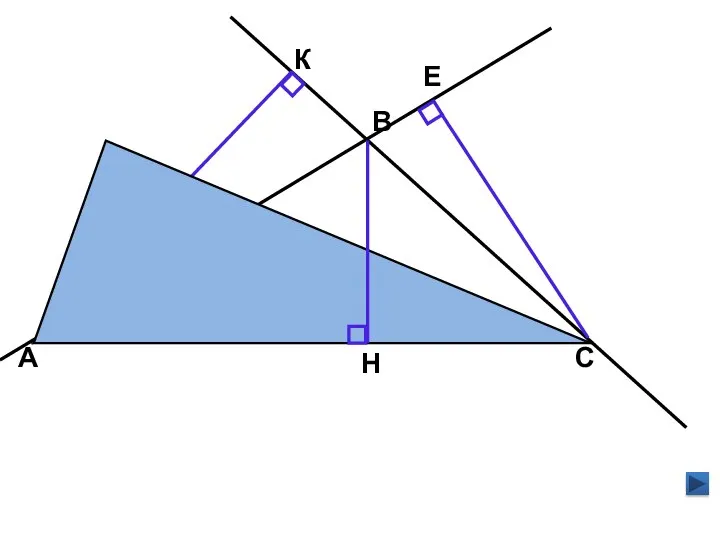
- 8. А С В Н К Е
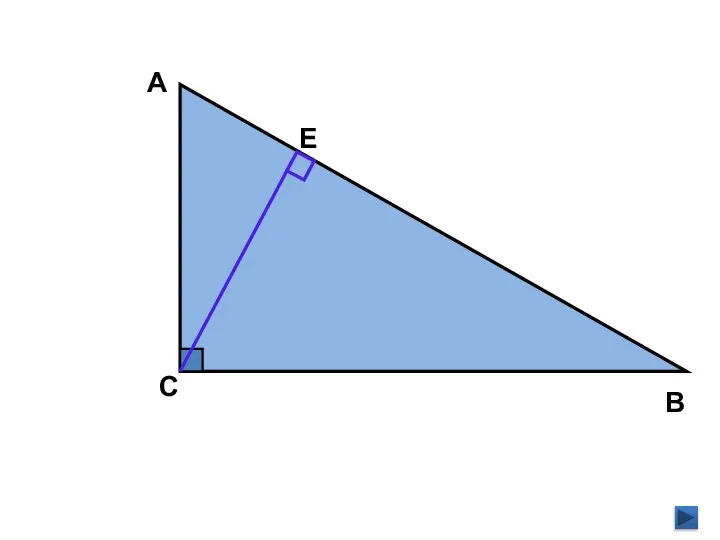
- 9. А В С Е
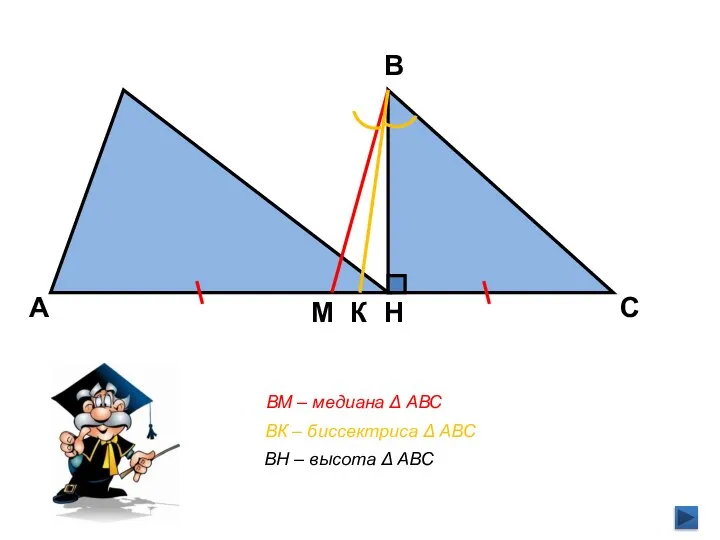
- 10. В С А Н ВК – биссектриса Δ АВС ВМ – медиана Δ АВС ВН –
- 11. МЕДИАНА ВЫСОТА БИССЕКТРИСА ПЕРПЕНДИКУЛЯР
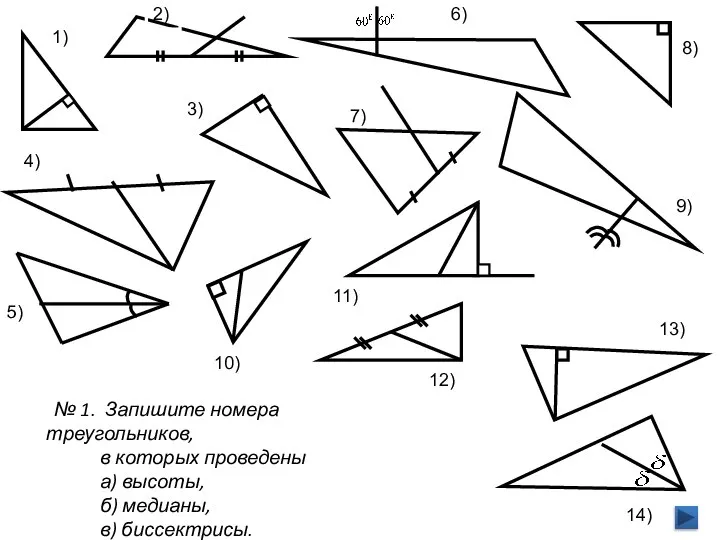
- 12. 2) 1) 5) 6) 7) 8) 9) 11) 12) 13) 14) 3) 4) 10) № 1.
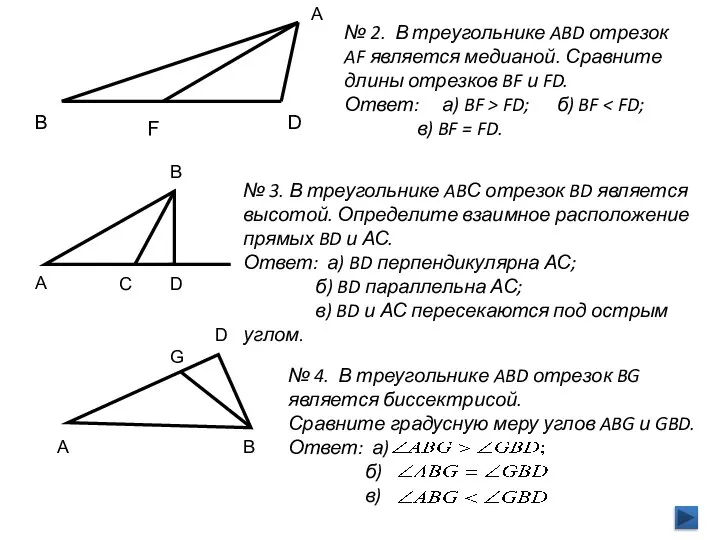
- 13. А В D F В A C D G A D В № 2. В треугольнике
- 15. Скачать презентацию

 Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ
Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ  Углы между прямыми и плоскостями (координатный метод), 11 класс
Углы между прямыми и плоскостями (координатный метод), 11 класс reshenie-trigonometricheskih-uravneniy-i-sposoby-otbora-korney-na-zadannom-promezhutke
reshenie-trigonometricheskih-uravneniy-i-sposoby-otbora-korney-na-zadannom-promezhutke Матрицы. Действия над матрицами
Матрицы. Действия над матрицами Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Призма и ее виды. Чертеж призмы
Призма и ее виды. Чертеж призмы Задача на спрос и предложение
Задача на спрос и предложение Круг, окружность, длина окружности. 6 класс
Круг, окружность, длина окружности. 6 класс Исследование на принадлежность классам функцию. Практическая работа
Исследование на принадлежность классам функцию. Практическая работа Раскраска графов. Лекция 07
Раскраска графов. Лекция 07 Probability Distributions
Probability Distributions Математические ребусы
Математические ребусы Cхема (метод) Горнера. Способ деления многочлена
Cхема (метод) Горнера. Способ деления многочлена Окружность Аполлония
Окружность Аполлония Угол между векторами
Угол между векторами Что такое математика?
Что такое математика? Арифметические действия
Арифметические действия Теорема. Франсуа Виет (1540-1603)
Теорема. Франсуа Виет (1540-1603) Квадратные уравнения. Основные понятия
Квадратные уравнения. Основные понятия Метрология, основные понятия
Метрология, основные понятия Урок-КВН
Урок-КВН Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Метрическая система мер
Метрическая система мер Основы анализа данных. Метод наименьших квадратов. (Лекция 6)
Основы анализа данных. Метод наименьших квадратов. (Лекция 6)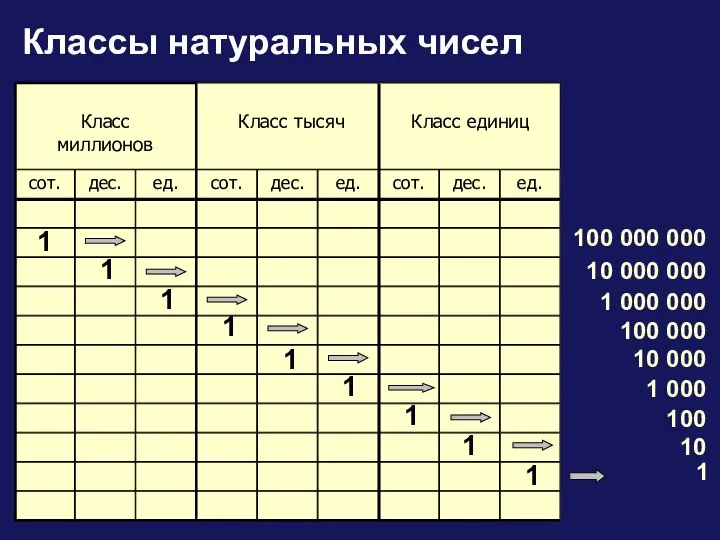 Классы натуральных чисел
Классы натуральных чисел Число и цифра 8
Число и цифра 8 Правильные многоугольники
Правильные многоугольники