Ускоренное умножение

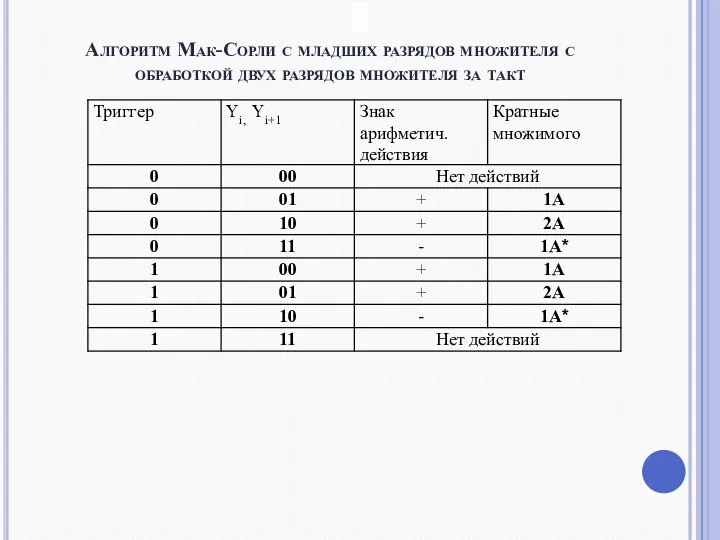
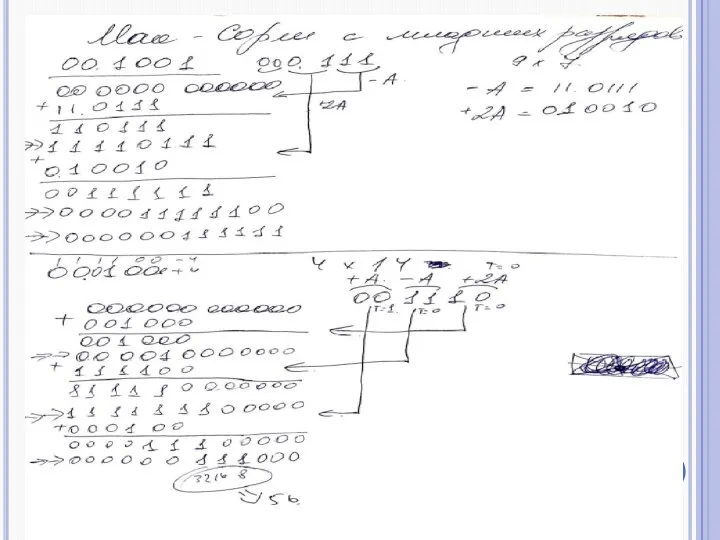
Алгоритм Мак-Сорли с младших разрядов множителя с обработкой двух разрядов множителя за такт

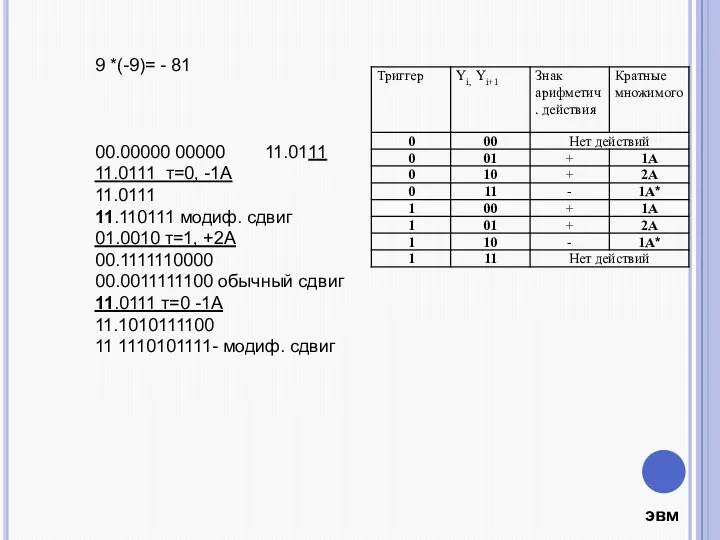
9 *(-9)= - 81
00.00000 00000 11.0111
11.0111 т=0, -1А
11.0111
11.110111 модиф. сдвиг
01.0010 т=1, +2А
00.1111110000
00.0011111100 обычный сдвиг
11.0111 т=0 -1A
11.1010111100
11 1110101111- модиф. cдвиг

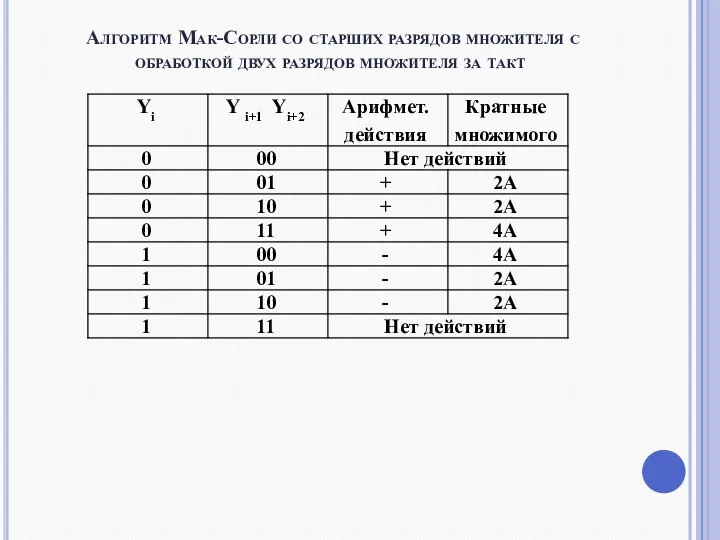
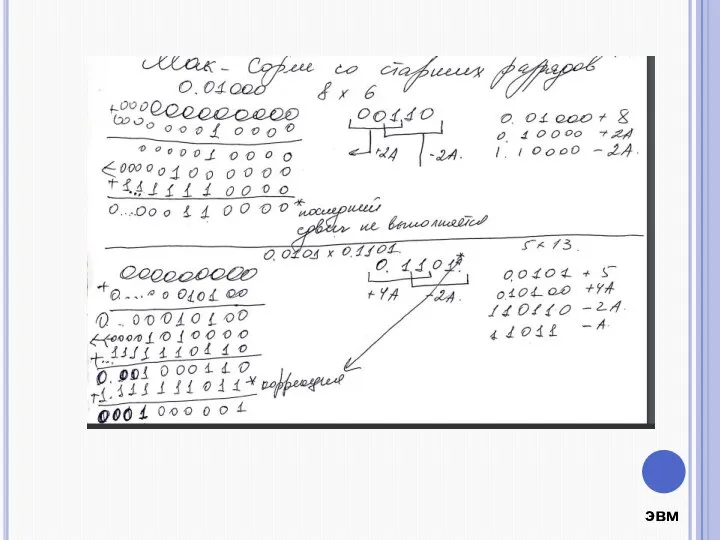
Алгоритм Мак-Сорли со старших разрядов множителя с обработкой двух разрядов множителя за такт

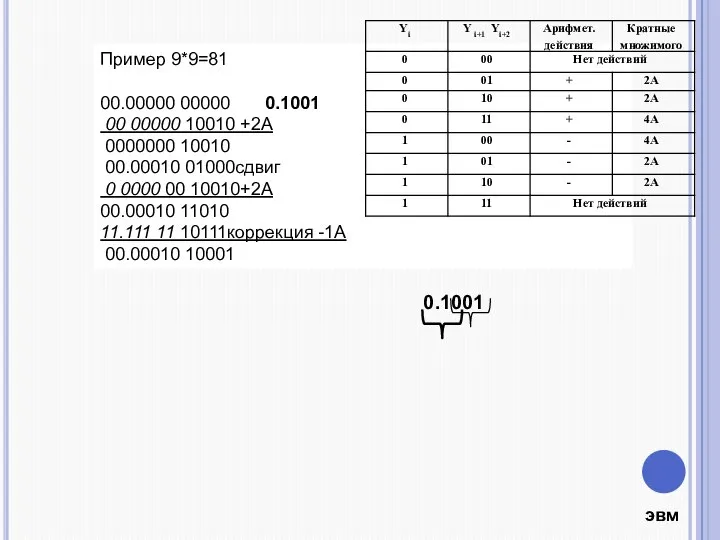
Пример 9*9=81
00.00000 00000 0.1001
00 00000 10010 +2А
0000000 10010 00.00010 01000сдвиг
0 0000 00 10010+2А
00.00010 11010
11.111 11 10111коррекция -1А
00.00010 10001
0.1001

,
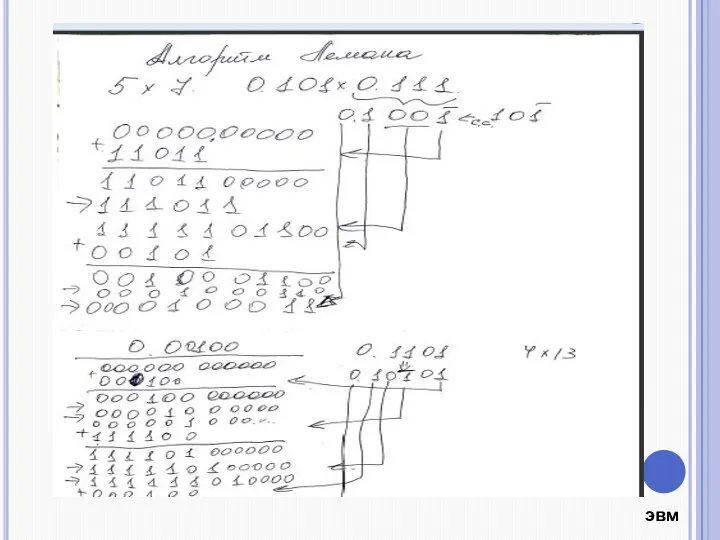
Алгоритм Лемана
На каждом шаге умножения выполняются действия, которые можно описать с помощью логических выражений :
0111== 1001

Основные этапы алгоритма
1. Прием сомножителей, запоминание знаков, формирование модулей.
2. Анализ сомножителей на 0. Формирование знака результата. Установка значения СчЦ.
3. Анализ младшего разряда множителя. Если младший разряд множителя равен 0, то производится сдвиг до появления первой 1. Если младший разряд множителя равен 1, то выполняется вычитание, если следующий разряд 1 и сложение, если следующий разряд 0.
4. Сдвиг суммы ЧП вправо на один разряд прямой или модифицированный сдвиг, если промежуточная сумма частичных произведений отрицательна.. Пункты З, 4 повторяются для всех цифровых разрядов множителя.
5. Формирование результата.
Пример: Разряды множителя 0111( b3 b2 b1 b0 )
,

10*7 01010 * 0.0111

Каждый элемент ai bj ( i, j = 1, n) принимает значение 0 или 1. Произведение A∙B может быть получено, если суммировать элементы матрицы .
Матричные методы умножения

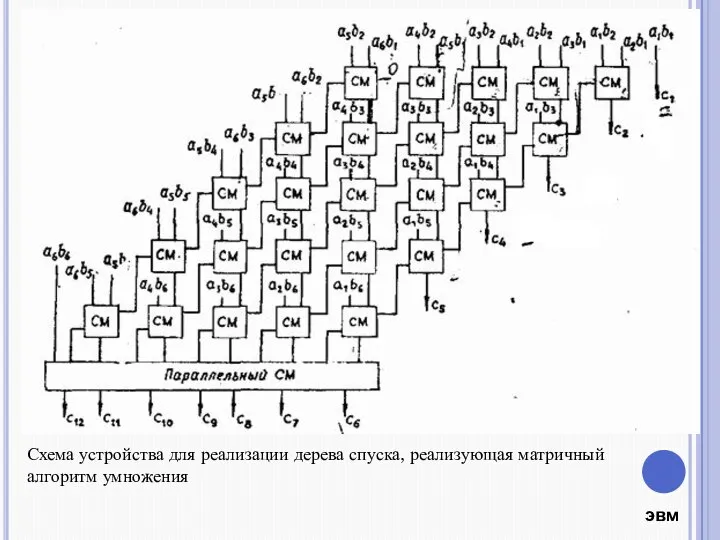
Схема устройства для реализации дерева спуска, реализующая матричный алгоритм умножения

Матричный умножитель п х п содержит п2 схем «И», n ПС и (п2 - 2п) СМ.
Если принять, что для реализации полусумматора требуются два логических элемента, а для полного сумматора — пять, то общее количество логических элементов в ум­ножителе составляет
п2 + 2п + 5(п2 – 2n) = 6n2 – 8n.
Полагая задержки в схеме «И» и полусумматоре равными θ, а в полном сумматоре — 2θ. общую задержку в умножителе можно оценить выражением {4n - 5)θ.

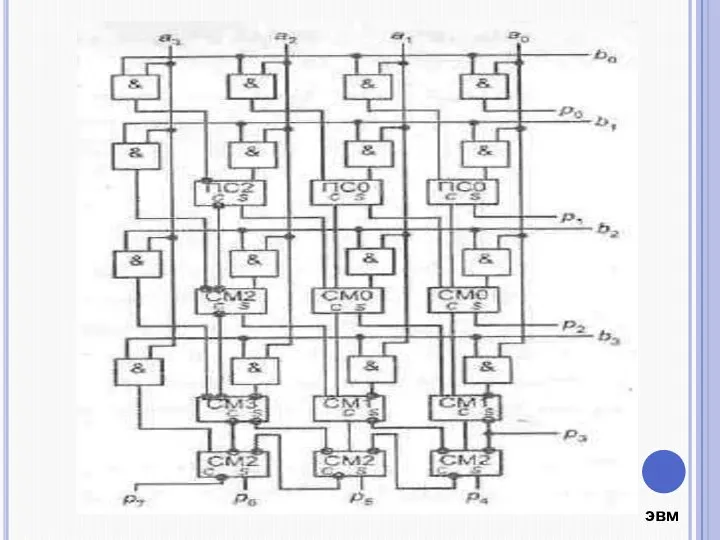
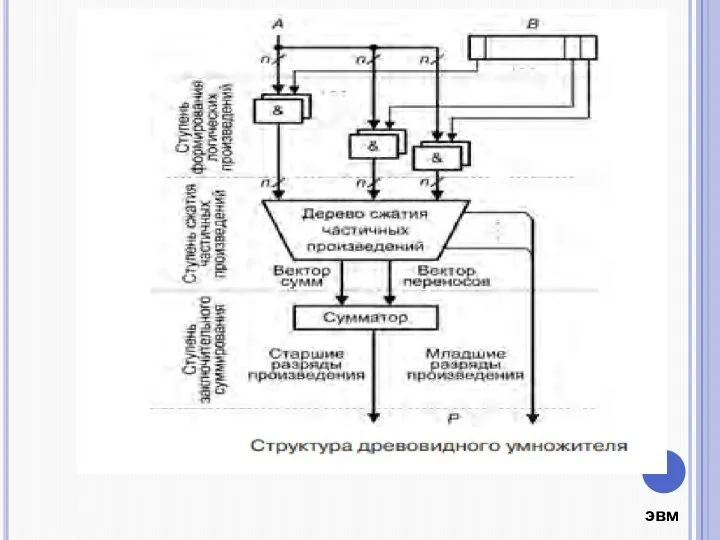
Древовидные умножители включают в себя три ступени:
- ступень формирования битов частичных произведений, состоящую из п2 эле­ментов «И»;
- ступень сжатия частичных произведений — реализуется в виде дерева параллельных сумматоров (накопителей), служащего для сведения частичных произведений к вектору сумм и вектору переносов. Сжатие реализуется несколькими рядами сумматоров, причем каждый ряд вносит задержку, свойственна одному полному сумматору;
- ступень заключительного суммирования, где осуществляется сложение вектора сумм и вектора переносов с целью получения конечного результата.

Суммирование ЧП с помощью дерева Уоллеса : а — логика суммирования; б — точечная диаграмма

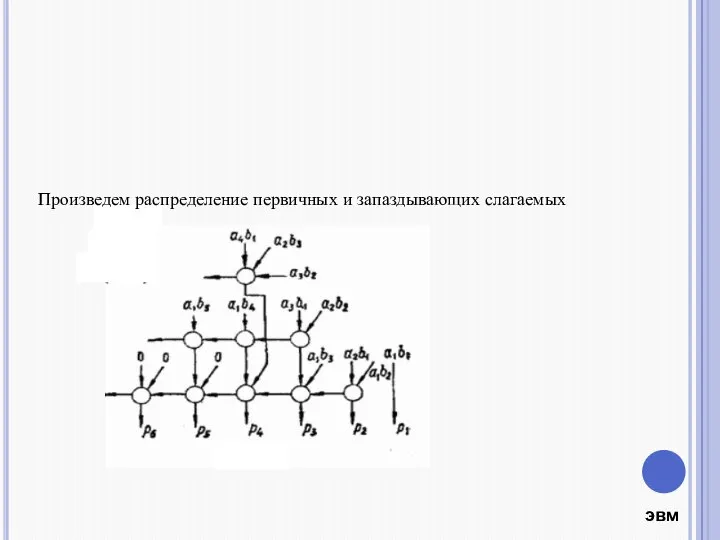
Произведем распределение первичных и запаздывающих слагаемых

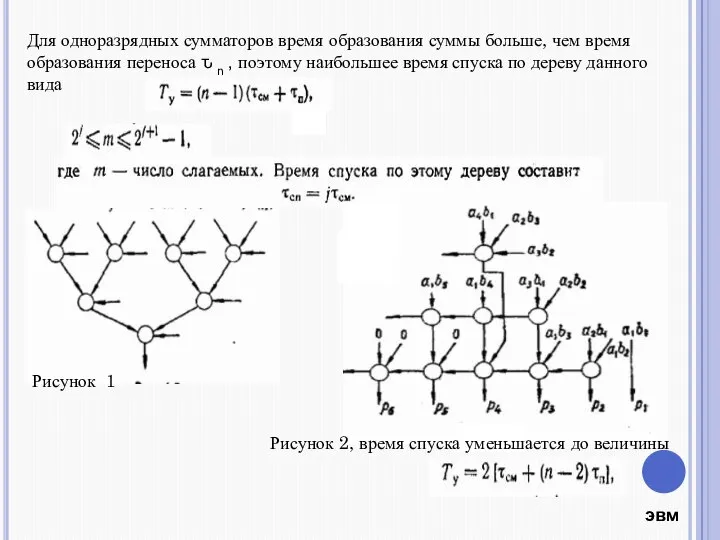
Для одноразрядных сумматоров время образования суммы больше, чем время образования переноса ԏ n , поэтому наибольшее время спуска по дереву данного вида
Рисунок 1
Рисунок 2, время спуска уменьшается до величины