Содержание
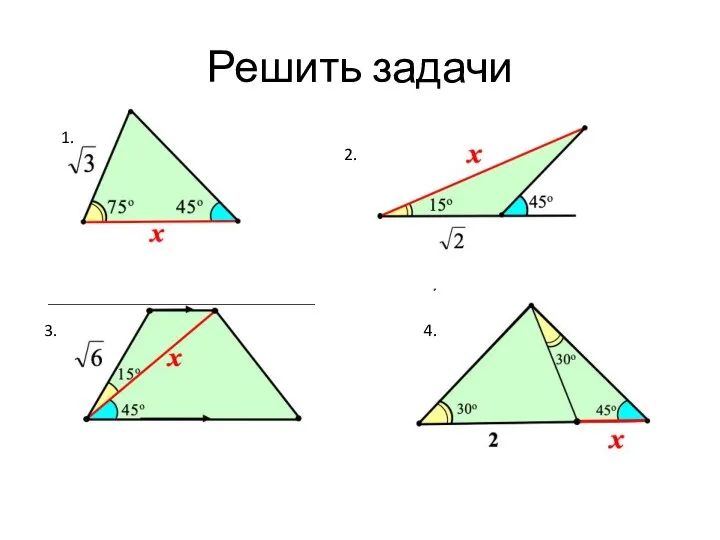
- 2. Решить задачи 1. 2. 3. 4.
- 3. ФОРМУЛЫ ДЛЯ ПЛОЩАДИ ТРЕУГОЛЬНИКА Если треугольник со сторонами а, b, c и углами α,β, γ вписан
- 4. Доказательство. Сначала докажем первую формулу.Возьмём известную формулу для площади треугольникаи подставим в неё выражения для его
- 5. ТЕОРЕМА ПТОЛЕМЕЯ Произведение диагоналей четырёхугольника,вписанного в окружность, равно сумме произведений двух пар его противоположных сторон. АС*ВД=
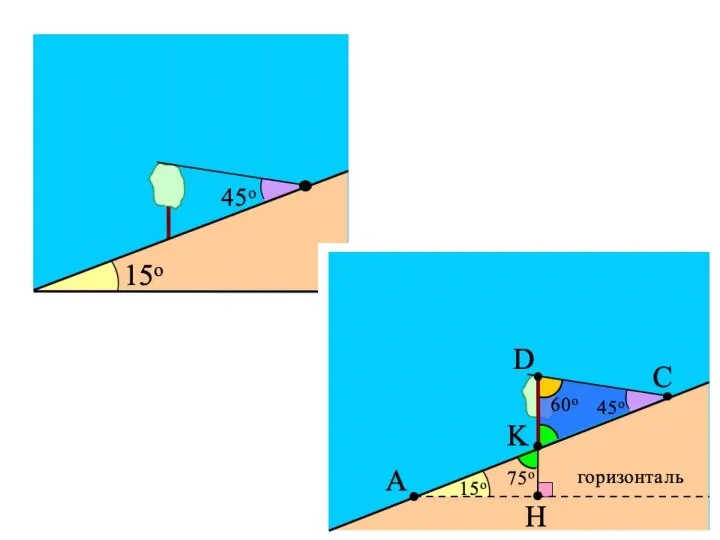
- 6. Примеры задач ПРИМЕР 1. (А) Человек видит дерево внизу на склоне холма под углом 45° по
- 7. Решение. Обозначим корень дерева буквой K, а его вершину – точкой D. Дерево растёт под прямым
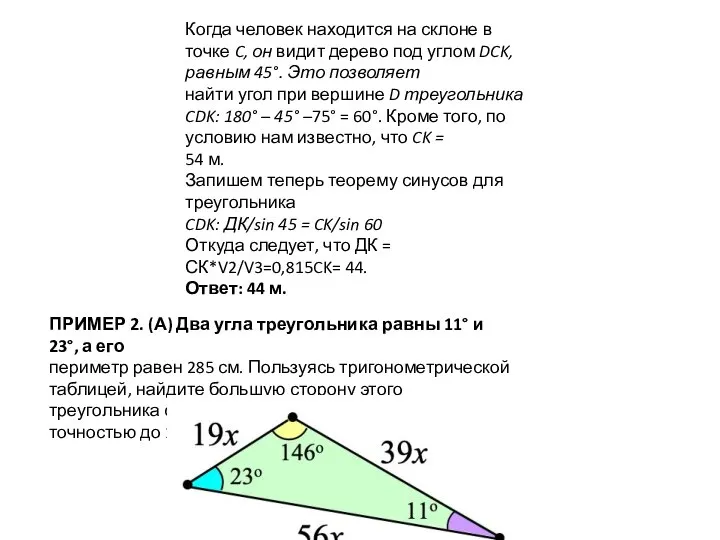
- 9. Когда человек находится на склоне в точке C, он видит дерево под углом DCK, равным 45°.
- 10. Решение. Сначала найдём третий угол данного треугольника. Его величина равна 180° – 11° – 23° =
- 11. приблизительно как 19 : 39 : 56. Значит, длины этих сторон можно обозначить как 19x, 39x
- 12. 1. (А) Два угла треугольника равны 16° и 30°. Его сторона, лежащая против большего из этих
- 14. Скачать презентацию








 Разбор заданий из ЕГЭ. Логарифмы
Разбор заданий из ЕГЭ. Логарифмы Математика учит точности мысли
Математика учит точности мысли Комплексные числа и координатная плоскость
Комплексные числа и координатная плоскость Презентация на тему Числовые выражения 7 класс
Презентация на тему Числовые выражения 7 класс  Урок-презентация по теме _Наибольший общий делитель. Взаимно простые числа_ (6 класс)
Урок-презентация по теме _Наибольший общий делитель. Взаимно простые числа_ (6 класс) множества дистант
множества дистант Интервальные оценки
Интервальные оценки Подготовка к ОГЭ, 9 класс, геометрия
Подготовка к ОГЭ, 9 класс, геометрия Линейная функция
Линейная функция Функции и их графики
Функции и их графики 5_vektory
5_vektory Квадратичная функция
Квадратичная функция Числовые домики. Тренажер
Числовые домики. Тренажер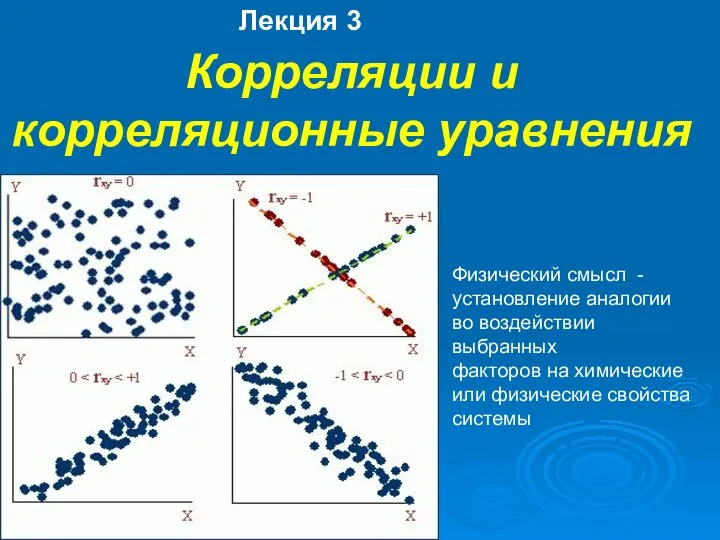 Корреляции и корреляционные уравнения
Корреляции и корреляционные уравнения Решение задач на проценты
Решение задач на проценты Веселые примеры
Веселые примеры Алгебраические уравнения
Алгебраические уравнения Линейная функция
Линейная функция Математическая логика
Математическая логика Личные местоимения
Личные местоимения Уравнения с модулем
Уравнения с модулем Методика изучения массы
Методика изучения массы Решение дробных рациональных уравнений. Алгебра 8 класс
Решение дробных рациональных уравнений. Алгебра 8 класс Логарифмические уравнения
Логарифмические уравнения Умножение смешанных дробей
Умножение смешанных дробей L_2_Zakony_logiki_ravnosilnye_preobrazovania_lektsia
L_2_Zakony_logiki_ravnosilnye_preobrazovania_lektsia Золотое сечение
Золотое сечение Геометрические фигуры
Геометрические фигуры