Содержание
- 2. Изобразите точку М, принадлежащую прямой b, и точки К, L, не принадлежащие прямой b. Сделайте соответствующие
- 3. - Изобразите прямую а, пересекающую плоскость α. Сделайте соответствующую запись.
- 4. Математический диктант 1). Сформулируйте аксиомы стереометрии: Аксиома 1. __________________________________________________________ _____________________________________________________________________ Аксиома 2. __________________________________________________________ _____________________________________________________________________ Аксиома 3.
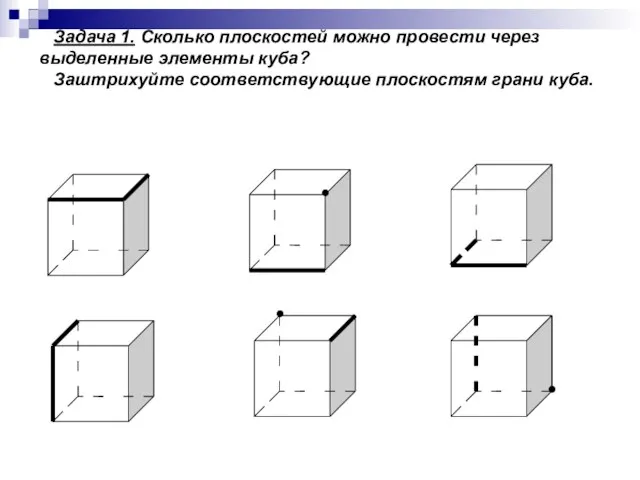
- 5. Задача 1. Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба. ●
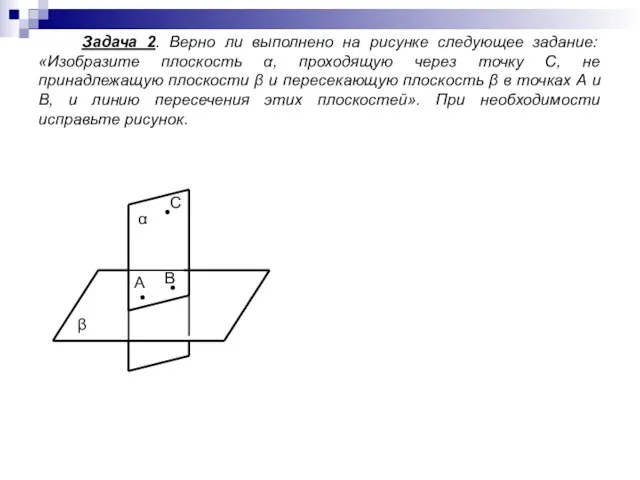
- 6. Задача 2. Верно ли выполнено на рисунке следующее задание: «Изобразите плоскость α, проходящую через точку С,
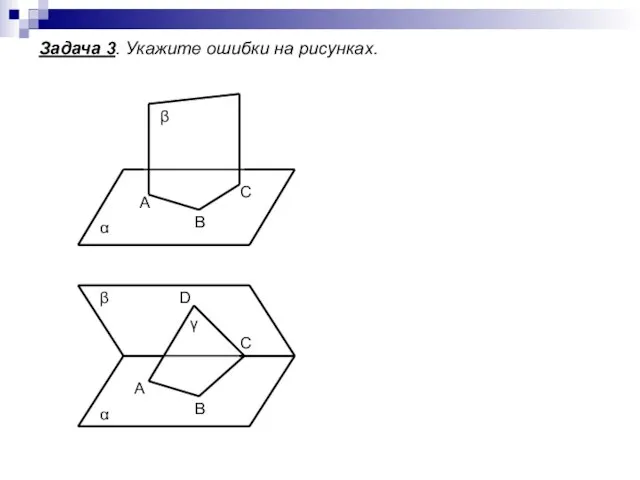
- 7. Задача 3. Укажите ошибки на рисунках. β β α α γ А В С А В
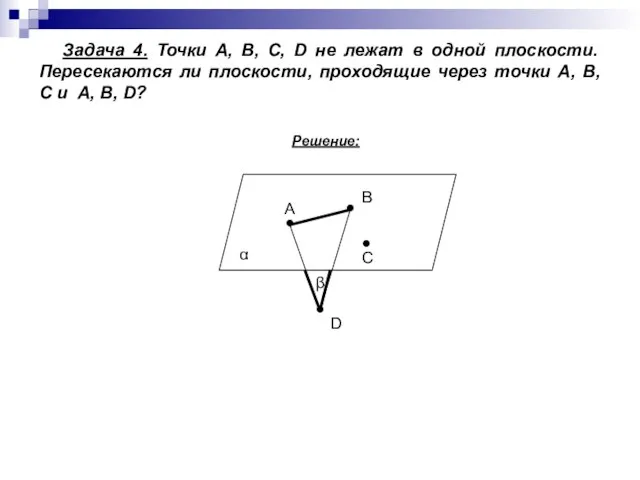
- 8. Задача 4. Точки А, В, С, D не лежат в одной плоскости. Пересекаются ли плоскости, проходящие
- 10. Скачать презентацию



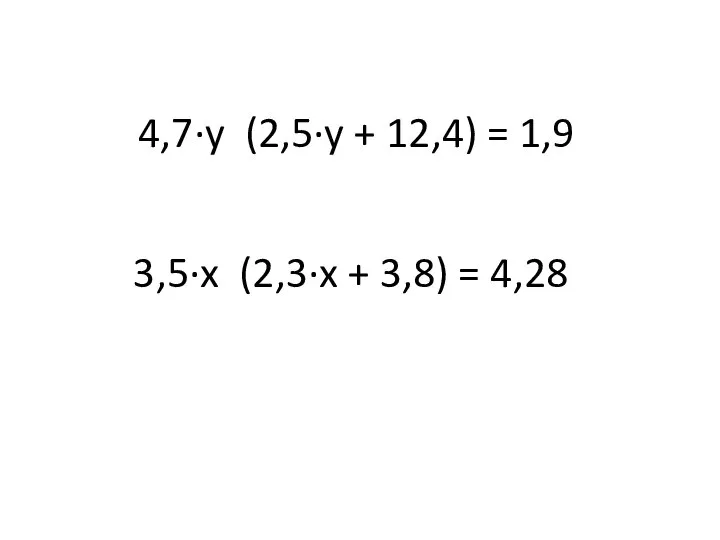 Учение о десятичных дробях
Учение о десятичных дробях Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Устная работа. Разложите на множители
Устная работа. Разложите на множители Факторный анализ торговых алгоритмов
Факторный анализ торговых алгоритмов Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Способы решения квадратных уравнений
Способы решения квадратных уравнений Вероятность случайного события. Математика
Вероятность случайного события. Математика Повторение курса геометрии. 7 класс
Повторение курса геометрии. 7 класс Графический диктант: Формулы
Графический диктант: Формулы Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И. Плоскость. Лекция 8
Плоскость. Лекция 8 Задача с экологическим содержанием
Задача с экологическим содержанием Реши самостоятельно
Реши самостоятельно Розв'язання задач
Розв'язання задач Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Свойства степени
Свойства степени График функции. Тест, 1-6 варианты
График функции. Тест, 1-6 варианты Матрицы. Прямоугольная таблица
Матрицы. Прямоугольная таблица Координатная плоскость. Задания для интерактивной доски
Координатная плоскость. Задания для интерактивной доски Естественный отбор и его математические характеристики
Естественный отбор и его математические характеристики Периметр, площадь, объём
Периметр, площадь, объём мощность множеств Леонгардт
мощность множеств Леонгардт Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений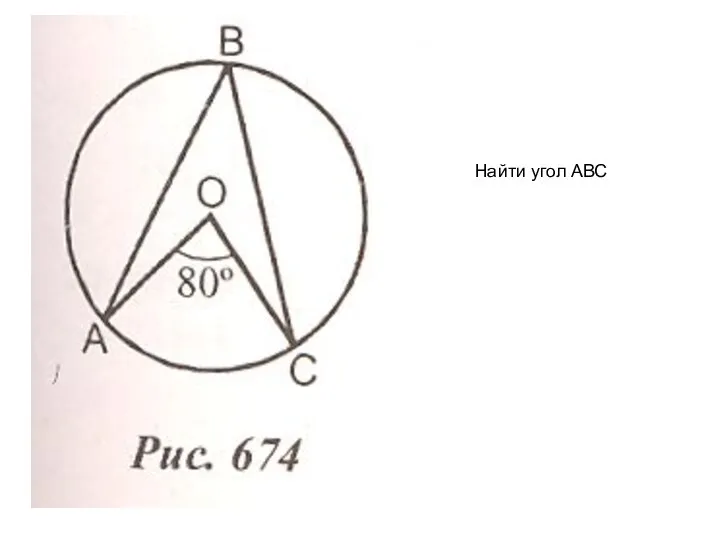 Найти угол АВС
Найти угол АВС Интеграл Лебега по измеримому в смысле Лебега множеству
Интеграл Лебега по измеримому в смысле Лебега множеству Приближенные значения чисел. Округление
Приближенные значения чисел. Округление В стране математики
В стране математики Задачи в координатах
Задачи в координатах