Естественный отбор и его математические характеристики

Цель урока:
Показать потенциальную возможность безграничного размножения особей популяции и ограниченность жизненных ресурсов
Убедиться в достоверности положений теории Дарвина
С помощью математического метода доказать, что естественный отбор – направленный эволюционный фактор.

План урока:
Интенсивность размножения особей и ее математическое выражение
Биологическое состязание как условие выживания
Естественный отбор и его количественные характеристики

Продуцирует в сутки 200 тыс. яиц.
3 тыс. семян 10 соцветий
За всю жизнь – 6 детенышей
За 750 лет – 19 млн.
До 10 млн. икринок за год

задача
Одно растение одуванчика занимает
Ѕ≈10м² и дает в год 100 летучих семян. Сколько км² площади покроет все потомство одной особи одуванчика через 10 лет, при условии, если он размножается беспрепятственно в геометрической прогрессии?

ОТВЕТ:
потомство одной особи одуванчика за 10 лет
ПРОБЛЕМА:
Хватит ли одуванчикам на 11 год места на Земле, если поверхность суши 148 млн. км2 (одно растение 10 м2)

Площадь Земли
Площадь,
которую заняли одуванчики на 11 год

Внутривидовая.
С неблагоприятными условиями среды.
Межвидовая.
Внутривидовая.

ВЫВОД:
Все формы борьбы за существование являются предпосылками естественного отбора, главный механизм которого заключается в выживании и размножении наиболее приспособленных особей за счет гибели менее приспособленных

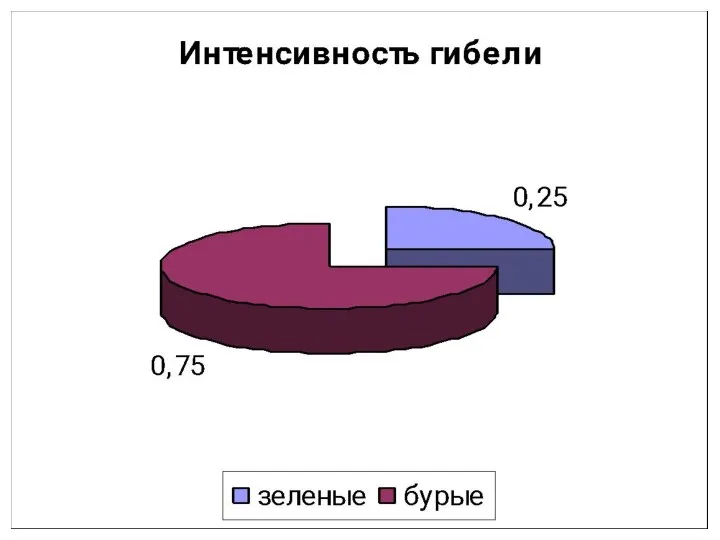
Естественный отбор и его математическая характеристика
Задача:
На дарвиновской площадке провели эксперимент: на зеленый покров выпустили 600 зеленых особей обыкновенного кузнечика и 600 бурых особей обыкновенного кузнечика.
Опыт показал, что птицы поедают 75% бурых особей и 25% зеленых. Определите коэффициент отбора. (f)

Для справки:
Е – интенсивность гибели
Е=m-n/n,
где m-начальное число особей
n-число особей выживших
S – коэффициент Е.О.
S=n2-n1/n1
где n2-число особей выживших зеленых
n1-бурых особей
F – эффективность отбора
f=n1(1+S)/1