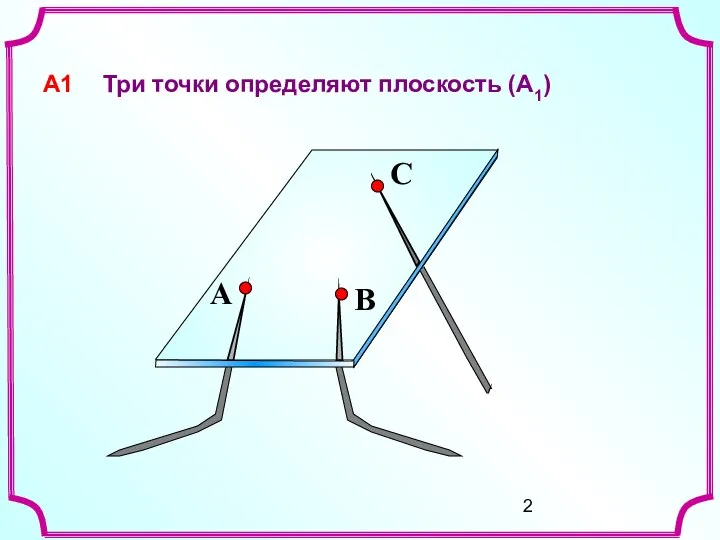
Содержание
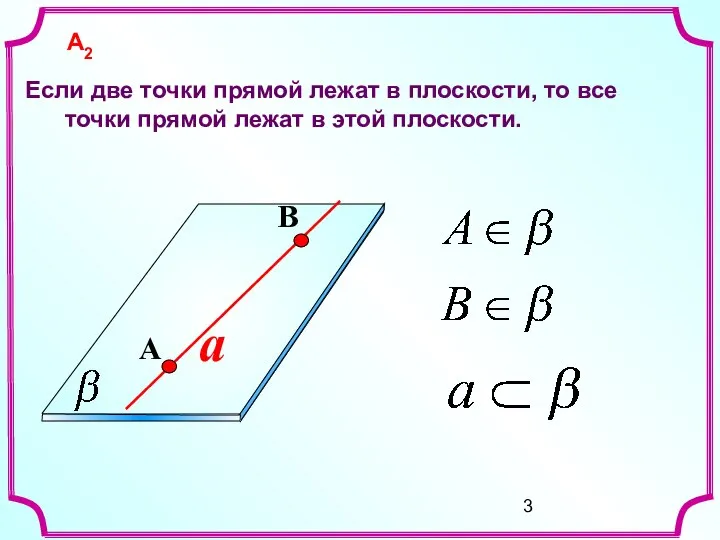
- 3. a Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
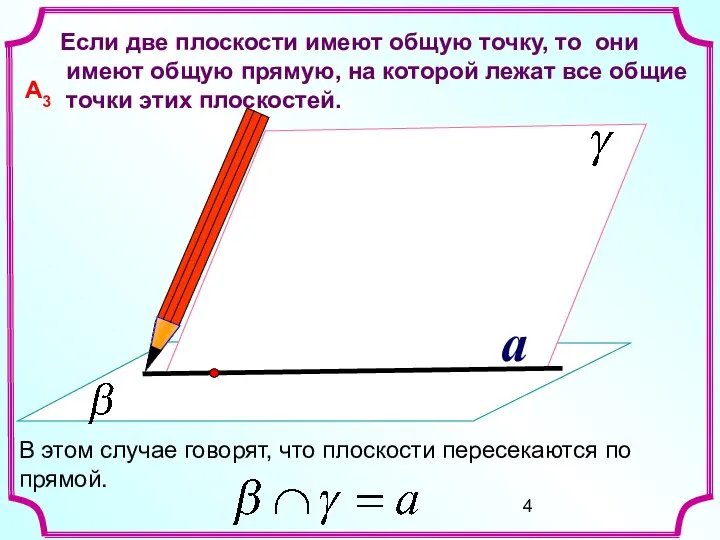
- 4. a Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все
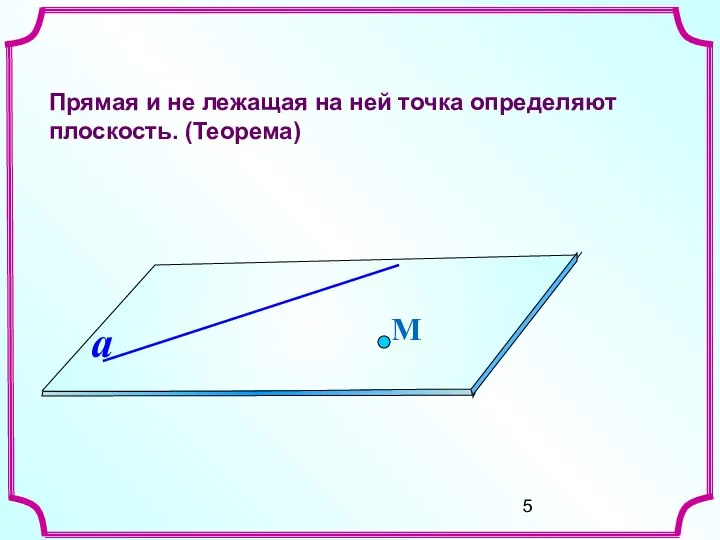
- 5. Прямая и не лежащая на ней точка определяют плоскость. (Теорема) М a
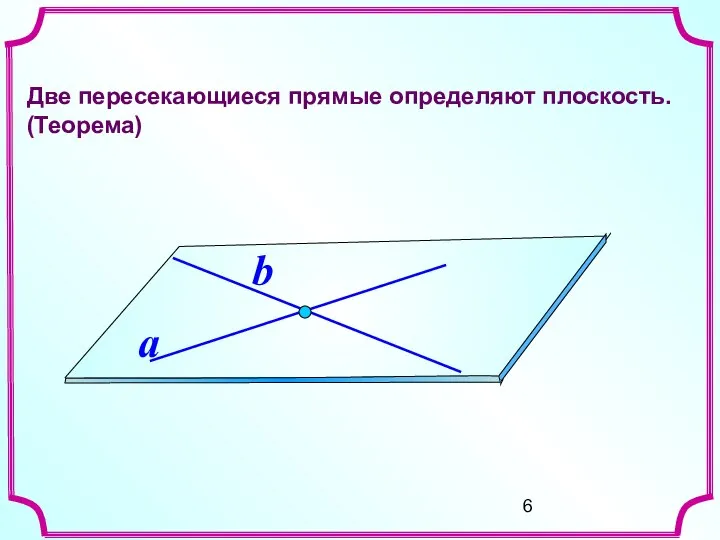
- 6. Две пересекающиеся прямые определяют плоскость. (Теорема) a b
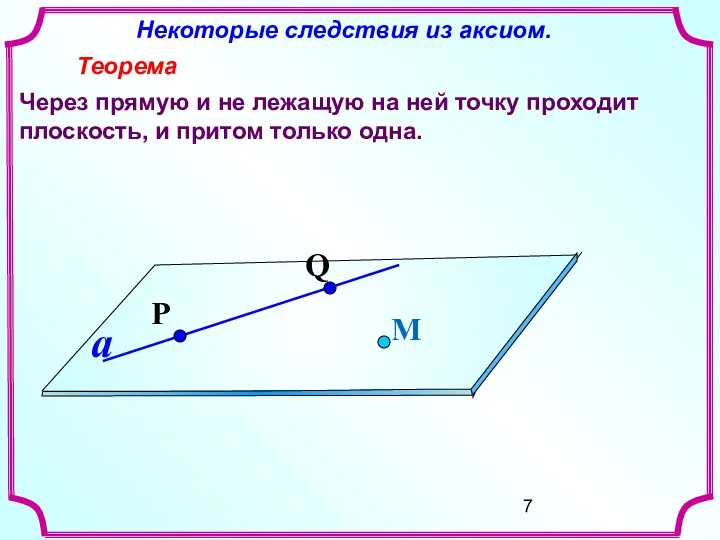
- 7. Некоторые следствия из аксиом. Теорема Через прямую и не лежащую на ней точку проходит плоскость, и
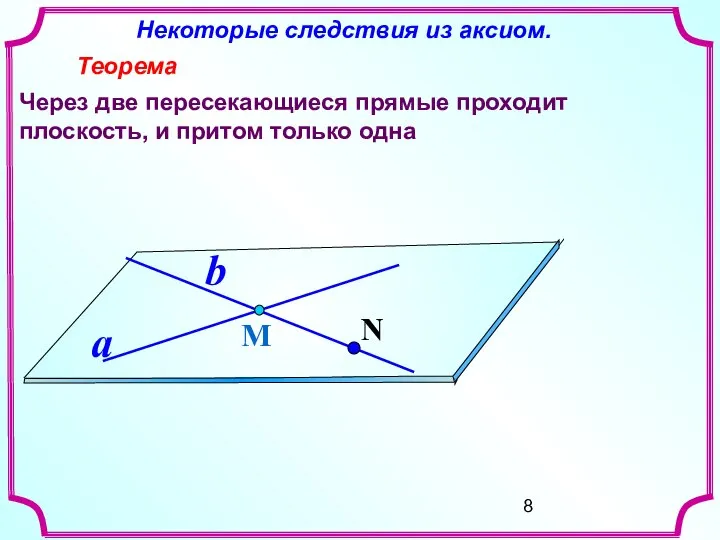
- 8. Некоторые следствия из аксиом. Теорема Через две пересекающиеся прямые проходит плоскость, и притом только одна М
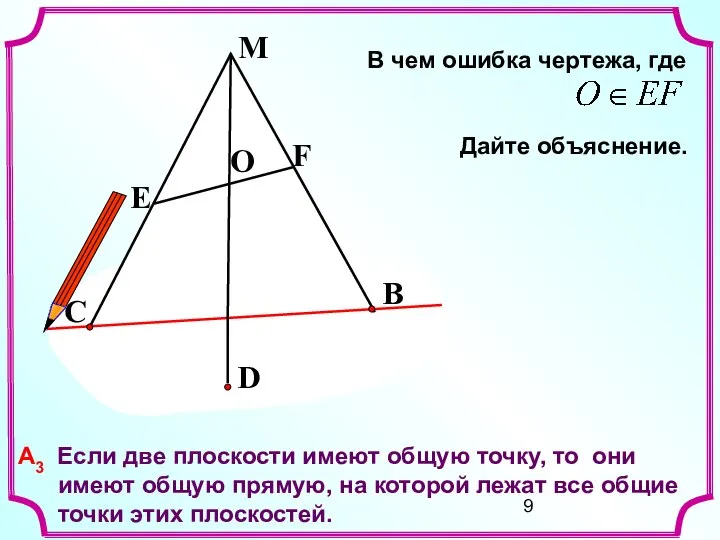
- 9. С Е М О F B D А3 Если две плоскости имеют общую точку, то они
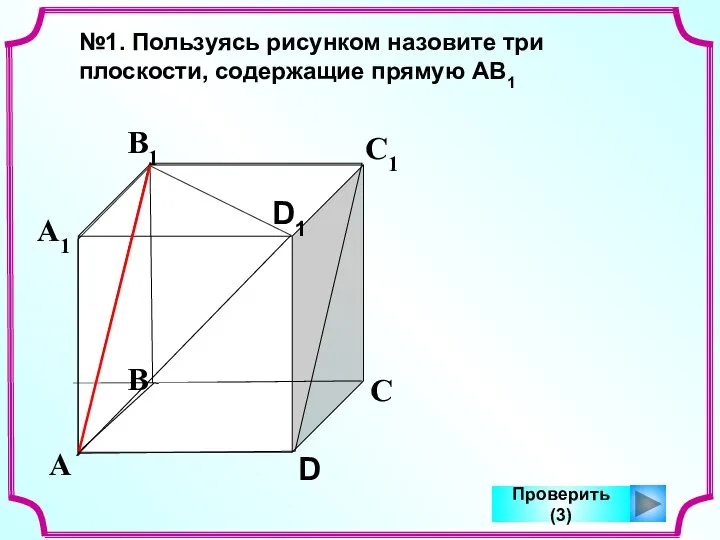
- 10. А В С D А1 В1 С1 D1 №1. Пользуясь рисунком назовите три плоскости, содержащие прямую
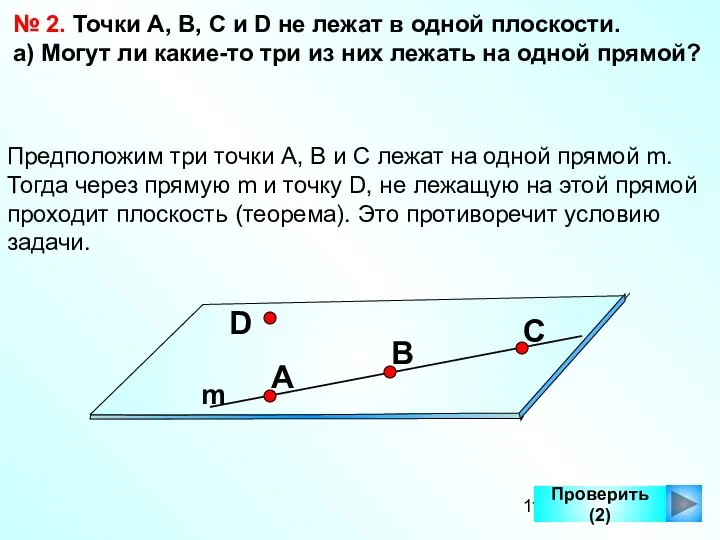
- 11. Проверить (2) № 2. Точки А, В, С и D не лежат в одной плоскости. а)
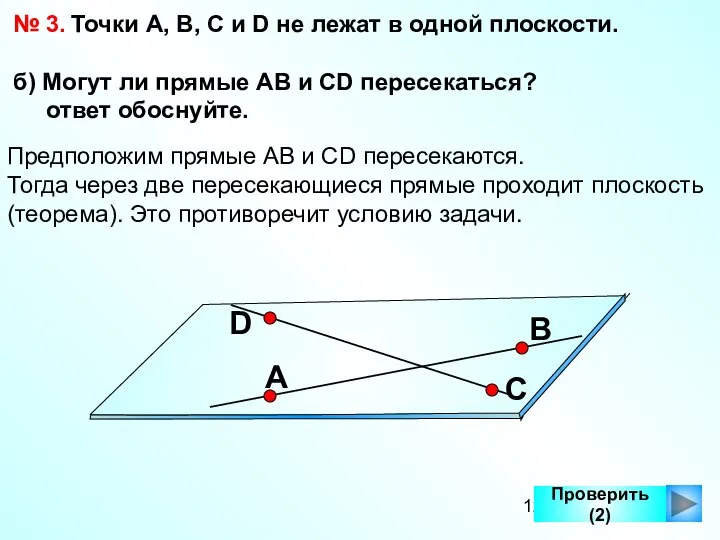
- 12. Проверить (2) № 3. Точки А, В, С и D не лежат в одной плоскости. б)
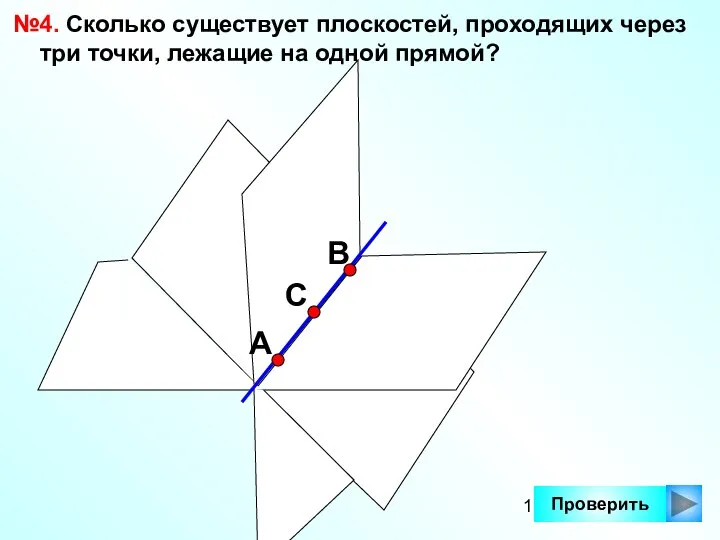
- 13. Проверить №4. Сколько существует плоскостей, проходящих через три точки, лежащие на одной прямой? А С В
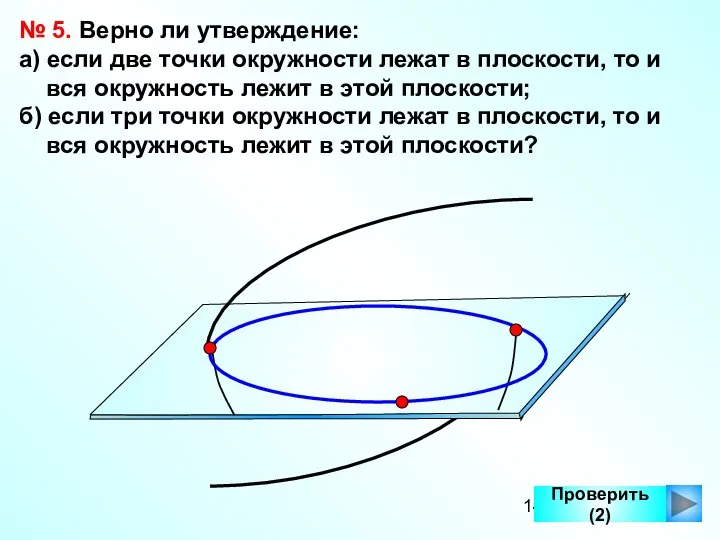
- 14. Проверить (2) № 5. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то
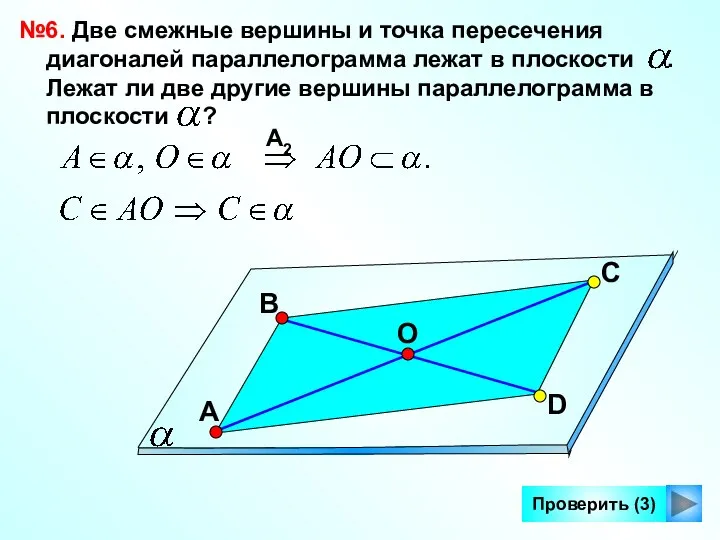
- 15. Проверить (3) №6. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат
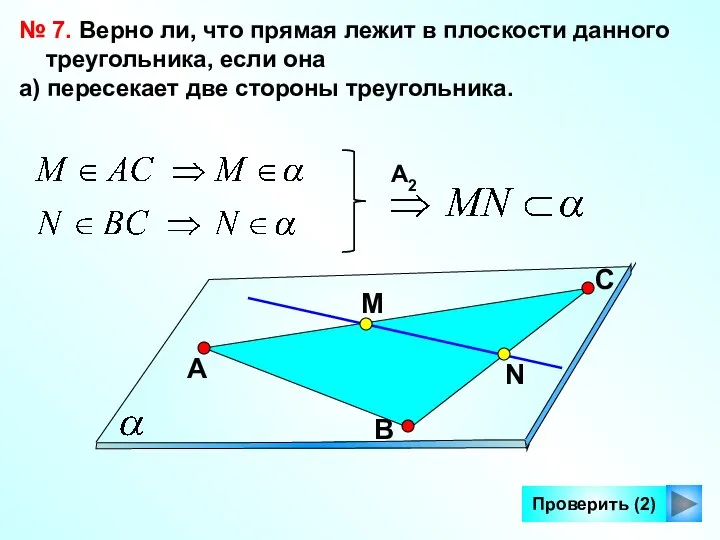
- 16. Проверить (2) № 7. Верно ли, что прямая лежит в плоскости данного треугольника, если она а)
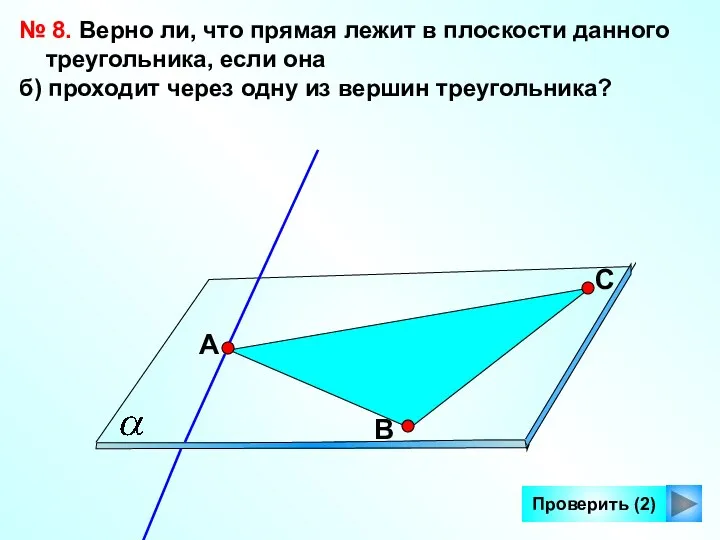
- 17. Проверить (2) № 8. Верно ли, что прямая лежит в плоскости данного треугольника, если она б)
- 19. Скачать презентацию
 Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2)
Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2) Решение уравнений. 7 класс
Решение уравнений. 7 класс Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты LP
LP Арифметическая прогрессия
Арифметическая прогрессия Разбор задания из ЕГЭ. Логарифмы
Разбор задания из ЕГЭ. Логарифмы Необыкновенное путешествие Зимы. Цифры для дошкольников
Необыкновенное путешествие Зимы. Цифры для дошкольников Симметрия
Симметрия Дифференциальные уравнения
Дифференциальные уравнения Занятие 1. Вводное занятие
Занятие 1. Вводное занятие Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Презентация на тему Уравнения
Презентация на тему Уравнения  Простейшие задачи в координатах
Простейшие задачи в координатах Число π. Длина окружности
Число π. Длина окружности Задачи на части
Задачи на части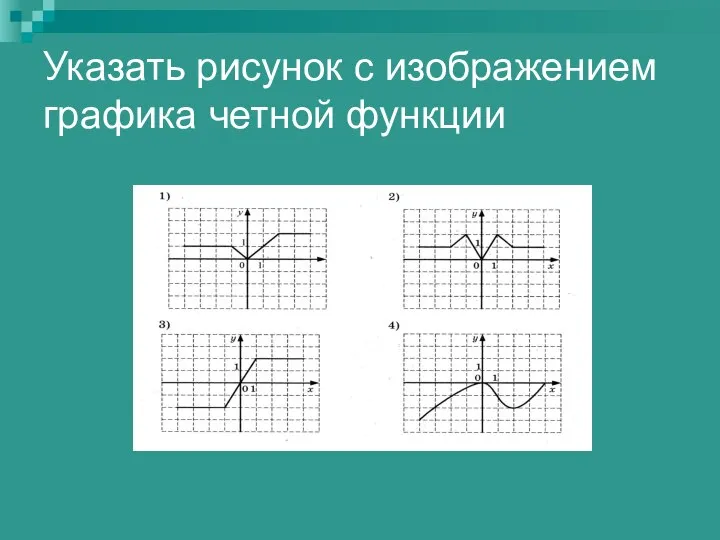 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Метрология. Погрешность измерений
Метрология. Погрешность измерений Изучение быстрого счёта с использованием нестандартных приёмов устного счёта
Изучение быстрого счёта с использованием нестандартных приёмов устного счёта Синус, косинус, тангенс и котангенс угла поворота
Синус, косинус, тангенс и котангенс угла поворота Составь задачу по картинке и реши ее. Который час?
Составь задачу по картинке и реши ее. Который час? Подготовка к ГИА по математике. Задания 6
Подготовка к ГИА по математике. Задания 6 Площадь прямоугольника
Площадь прямоугольника Понятие о комплексных числах. Рациональные функции одной переменной. Лекция 14
Понятие о комплексных числах. Рациональные функции одной переменной. Лекция 14 Matplotlib
Matplotlib Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45 Теорема косинусов
Теорема косинусов Вписанная и описанная окружность. 9 класс
Вписанная и описанная окружность. 9 класс