Применение графов для решения логических задач

В последнее время интерес к комбинаторике в школьном курсе математики заметно возрос. Элементы комбинаторики, статистики и теории вероятностей включены в новые стандарты по математике для основной и профильной школ. Формирование комбинаторных представлений и развитие комбинаторного мышления школьников входит в число основных целей обучения математике.
Однако обычно, когда говорят об элементах комбинаторики, имеют в виду задачи алгебраического содержания. Здесь мы рассмотрим комбинаторные задачи, которые можно решать с помощью графов.

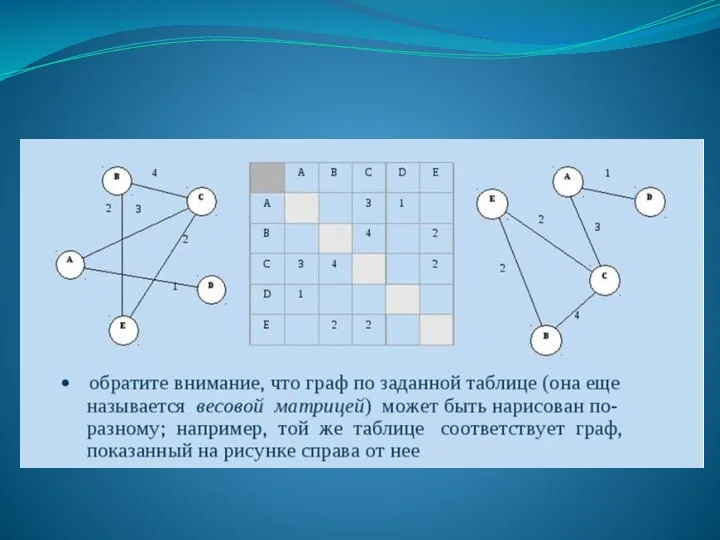
Соответствие таблицы и графов

Связность графа
Определение. Граф называется связным, если две его вершины могут быть соединены путем, т. е. последовательностью ребер, каждое следующее из которых начинается в конце предыдущего.
Определение. Несвязный граф состоит из нескольких «кусков».
Эти «куски» называются компонентами связности графа. Каждая компонента несвязного графа является, конечно, связным графом.

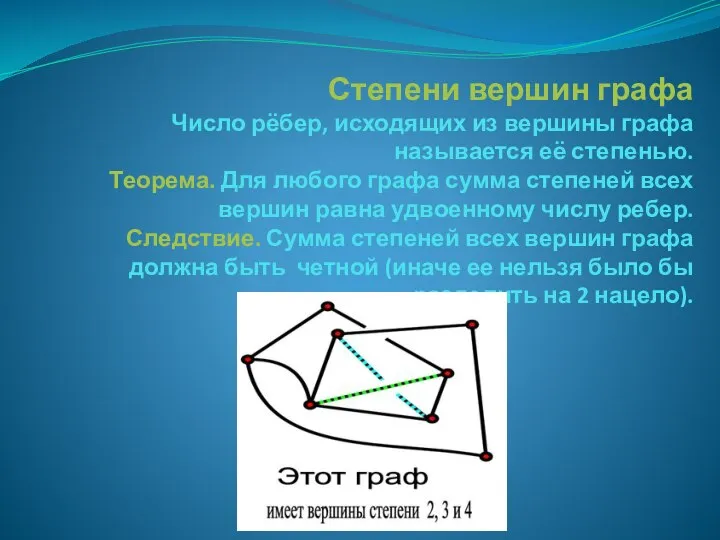
Степени вершин графа
Число рёбер, исходящих из вершины графа называется её степенью.
Теорема. Для любого графа сумма степеней всех вершин равна удвоенному числу ребер.
Следствие. Сумма степеней всех вершин графа должна быть четной (иначе ее нельзя было бы разделить на 2 нацело).

Графы в стратегии игр
Применяя граф- дерево можно разрабатывать выигрышные стратегии игр.
Задача12( ЕГЭ 2008).