Слайд 5Площадь плоской фигуры
Геометрический смысл определённого интеграла заключается в нахождении площади криволинейной трапеции

по формуле Ньютона-Лейбница:
Слайд 6Площадь плоской фигуры
Случаи:

Слайд 7Площадь плоской фигуры
Случаи:
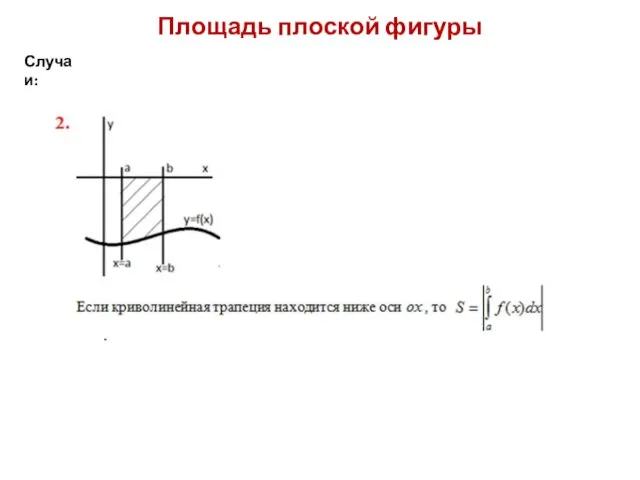
Слайд 8Площадь плоской фигуры
Случаи:
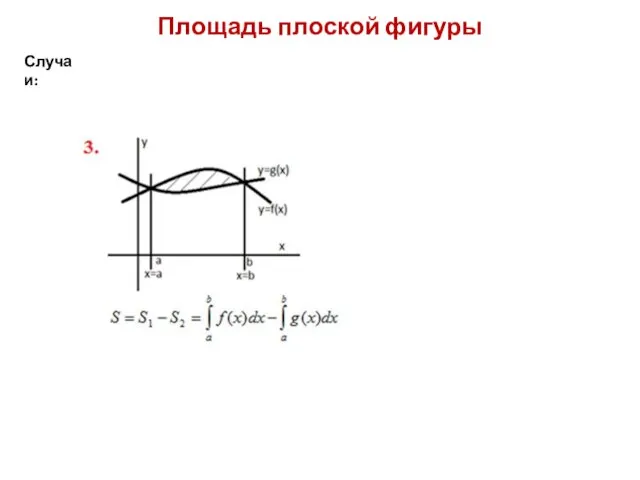
Слайд 9Площадь плоской фигуры
Случаи:
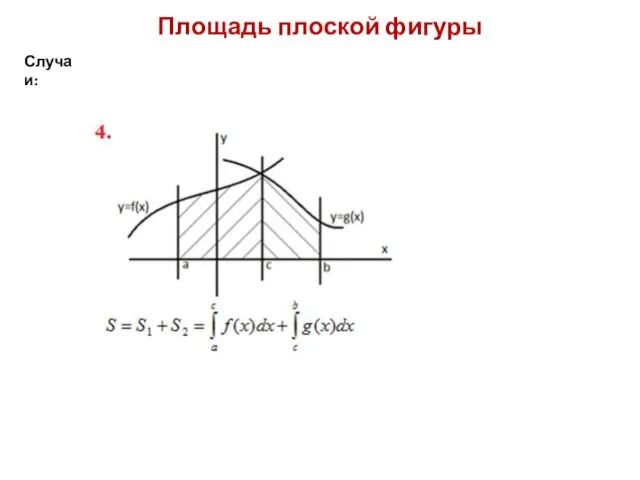
Слайд 10Задача 1: Вычислите площадь фигуры, ограниченной линиями
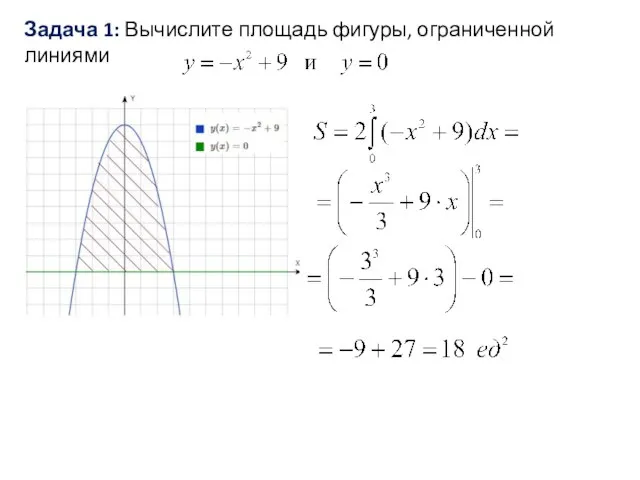
Слайд 11Задача 2: Вычислите площадь фигуры, ограниченной линиями
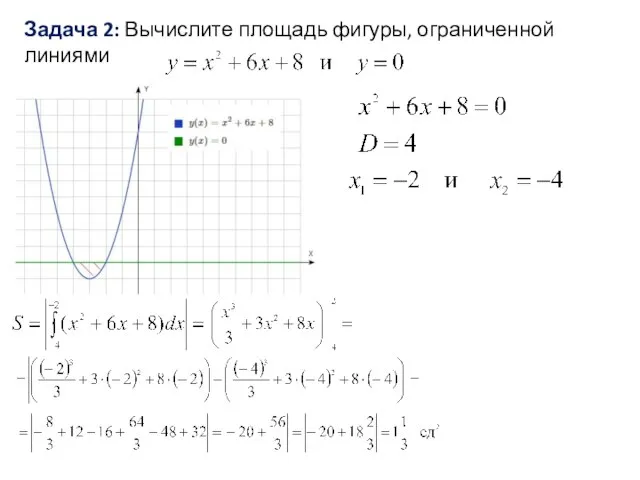
Слайд 12Задача 3: Вычислите площадь фигуры, ограниченной линиями
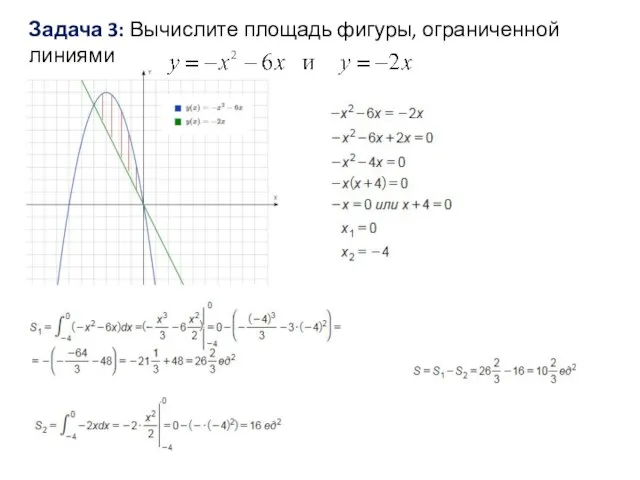
Слайд 13Задача 4: Вычислите площадь фигуры, ограниченной линиями
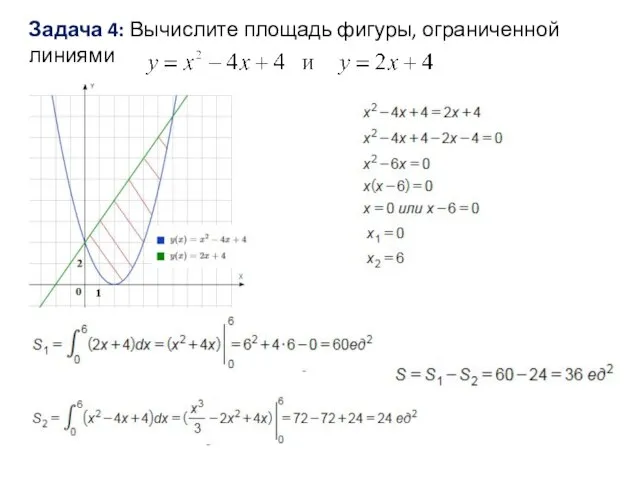
Слайд 14Задача 5: Вычислите площадь фигуры, ограниченной линиями
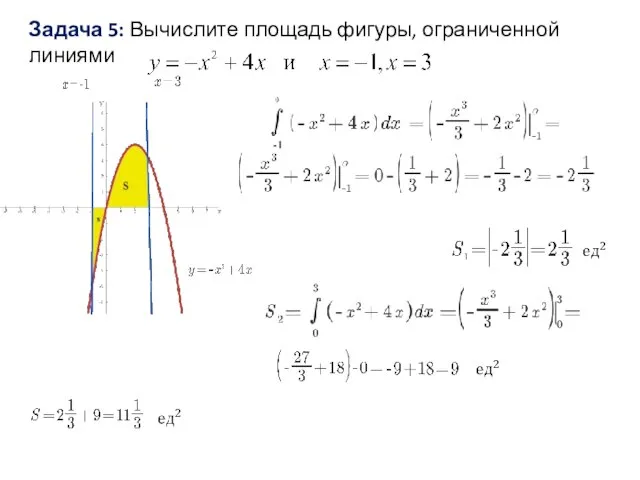













 Математический маятник. Измерения
Математический маятник. Измерения Признаки равенства треугольников
Признаки равенства треугольников Пропорция
Пропорция Решение текстовых задач
Решение текстовых задач Цифра ноль
Цифра ноль Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Решение задач с помощью уравнений
Решение задач с помощью уравнений Число и цифра 5
Число и цифра 5 Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Число π. Длина окружности
Число π. Длина окружности Теория игр
Теория игр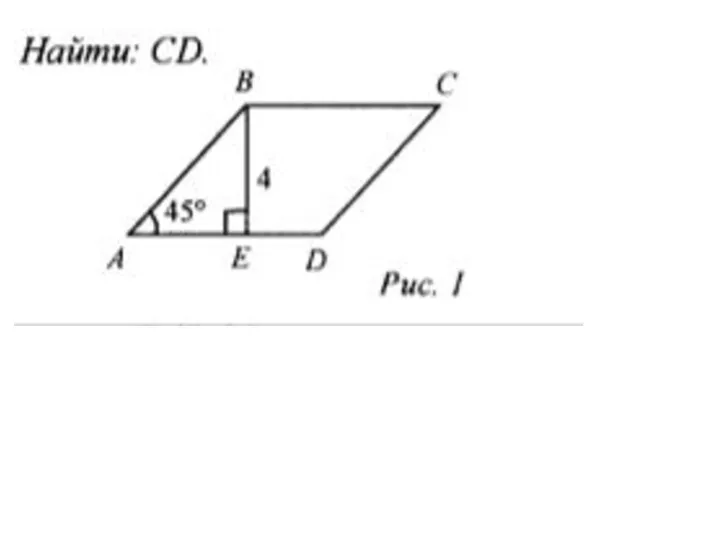 Вычисление площадей
Вычисление площадей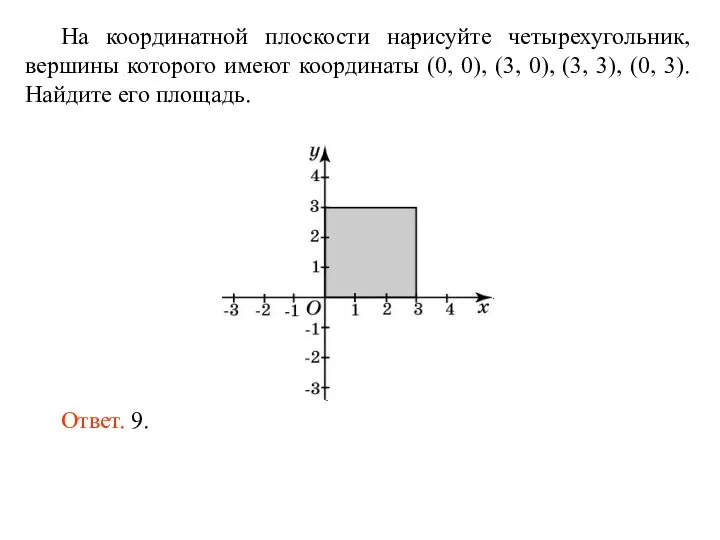 Площадь фигур на координатной плоскости
Площадь фигур на координатной плоскости Распределительная логистика. Практическое задание №8
Распределительная логистика. Практическое задание №8 Окружность. Методическая разработка урока
Окружность. Методическая разработка урока История дробей
История дробей Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Случаи вычитания 11-
Случаи вычитания 11- Функция. Свойства функции
Функция. Свойства функции Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Математика в профессиях
Математика в профессиях Симметрия
Симметрия Взятие Измаила в математических и исторических нюансах
Взятие Измаила в математических и исторических нюансах Векторы. Решение задач
Векторы. Решение задач Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Треугольник
Треугольник Четность, нечетность синуса, косинуса, тангенса, котангенса
Четность, нечетность синуса, косинуса, тангенса, котангенса