Линейная алгебра. Применение определителей

§1. НАХОЖДЕНИЕ РАНГА МАТРИЦЫ
Пусть A - прямоугольная матрица размера mxn
Пусть в матрице A произвольным образом выбраны l строк и l столбцов, где l ≤ min(m;n). Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу l -го порядка, определители которой называются минорами l -го порядка матрицы A.
Рангом матрицы A (обозначение - r(A)или rangA) называется максимальный порядок миноров данной матрицы, не равных нулю. Минор, определяющий ранг матрицы, называется базисным.
У матрицы базисный минор определяется неоднозначно.

Решение. Поскольку у матрицы A два нулевых столбца, то все миноры 3-го порядка равны нулю. Существует минор 2-го порядка, стоящий на пересечении 1-ой и 2-ой строк и 2-го и 3-го столбцов, неравный нулю:
Поэтому, rangA=2. Данный минор является одним из базисных.
Из определения ранга матрицы следуют его свойства:
1. rangA ≤ min(m;n), т.е. ранг матрицы не превосходит меньшего из ее размеров.

2. rangA=0 тогда и только тогда, когда A - нулевая матрица.
3. Ранг матрицы не изменится, если из нее вычеркнуть все нулевые строки и столбцы.
4. Ранг матрицы не изменится при её транспонировании.
5. Элементарные преобразования матрицы не меняют её ранга.
Пример 2. Найти ранг матрицы
Решение. В результате элементарных преобразований
и применения свойств ранга получаем каноническую
матрицу вида
поэтому, ранг матрицы A равен rangA = 2.

§2. ОБРАТНАЯ МАТРИЦА И ЕЕ НАХОЖДЕНИЕ
Пусть дана квадратная матрица порядка n :
Квадратная матрица A−1 порядка n называется обратной к матрице A, если выполняется условие: A⋅ A−1 = A−1 ⋅ A = E , где E - единичная матрица n -ого порядка.
Матрица A называется вырожденной (особенной), если её определитель равен нулю. Иначе, матрица A называется невырожденной.
Присоединенной матрицей или матрицей союзной к матрице A, называется матрица вида:
где Aij - алгебраические дополнения элементов aij матрицы A.

Теорема 1. Для того, чтобы у матрицы A существовала обратная, необходимо и достаточно, чтобы исходная матрица A была невырожденная.
Доказательство необходимости. Пусть матрица A имеет обратную матрицу A−1 ,
т.е. справедливо равенство A⋅ A−1 = A−1 ⋅ A = E .
Применим к данному равенству свойство 11 определителей.
Имеем |A⋅ A−1| = |A| ⋅ |A−1| = |E |=1, отсюда вытекает, что |A |≠ 0 и |A−1 |≠ 0.
Доказательство достаточности.
Для доказательства используем присоединенную матрицу.
Не теряя общности, докажем теорему для случая n = 3. Пусть

Присоединенная матрица AV имеет вид:
Вычислим их произведение A⋅ AV :

Тогда имеем: A⋅ AV = det A⋅ E . Аналогично рассуждая, получаем что AV⋅ A = det A⋅ E .
Полученные равенства представим в виде:
Тогда имеем, что
Что и требовалось доказать.
Пример1. Найти матрицу A−1, если
Решение. Имеем det A = −4. Найдем алгебраические дополнения соответствующих элементов матрицы A:

Очевидно:
Составим присоединенную матрицу

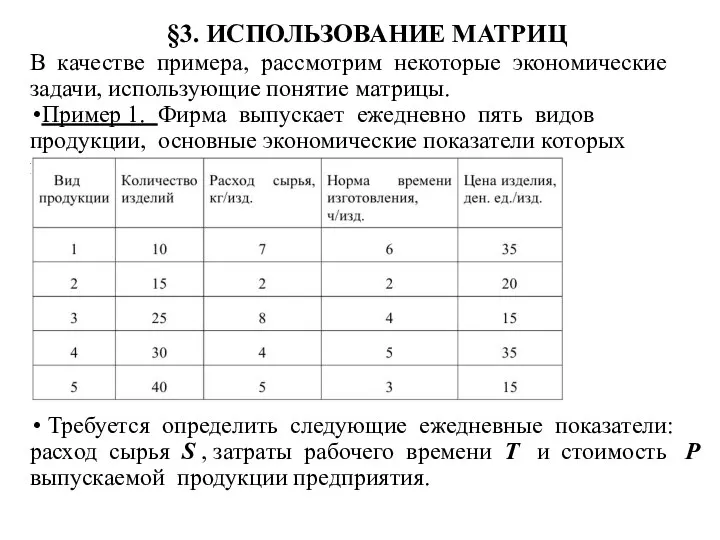
§3. ИСПОЛЬЗОВАНИЕ МАТРИЦ
В качестве примера, рассмотрим некоторые экономические задачи, использующие понятие матрицы.
Пример 1. Фирма выпускает ежедневно пять видов продукции, основные экономические показатели которых приведены в таблице
Требуется определить следующие ежедневные показатели: расход сырья S , затраты рабочего времени T и стоимость P выпускаемой продукции предприятия.

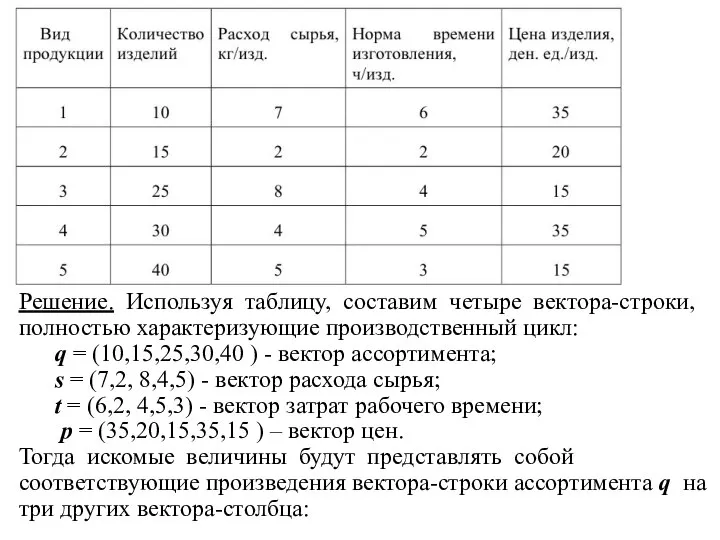
Решение. Используя таблицу, составим четыре вектора-строки, полностью характеризующие производственный цикл:
q = (10,15,25,30,40 ) - вектор ассортимента;
s = (7,2, 8,4,5) - вектор расхода сырья;
t = (6,2, 4,5,3) - вектор затрат рабочего времени;
p = (35,20,15,35,15 ) – вектор цен.
Тогда искомые величины будут представлять собой соответствующие произведения вектора-строки ассортимента q на три других вектора-столбца:

Пример 2. Компания выпускает четыре вида изделий, используя четыре вида сырья, нормы расхода которого даны как элементы матрицы A:
Определить затраты сырья каждого вида при плане выпуска каждого вида изделия: соответственно 30, 20, 40 и 50 ед.