Содержание
- 3. Любой вектор можно разложить по координатным векторам, т.е. представить в виде: Нулевой вектор также можно представить
- 4. Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной
- 5. Координаты середины отрезка Длина вектора по его координатам:
- 6. Даны векторы: Найти вектор, равный: Найдите значения m и n, при которых векторы коллинеарны.
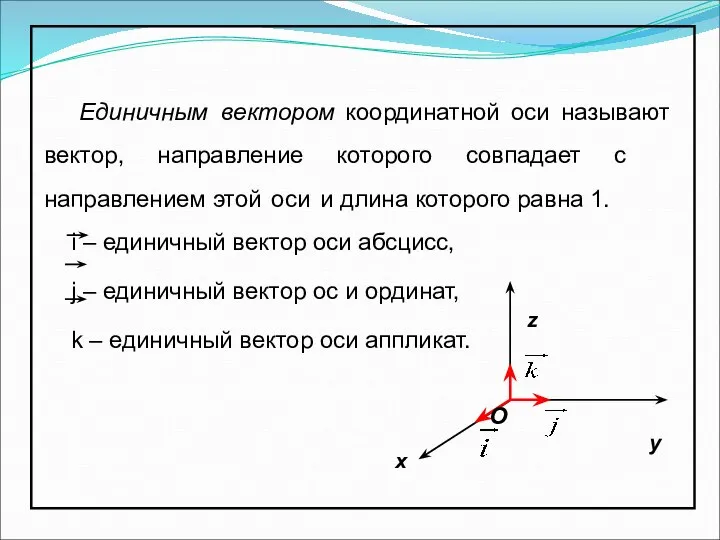
- 7. О А В α Если и ,то Если и , то. Если , то Угол между
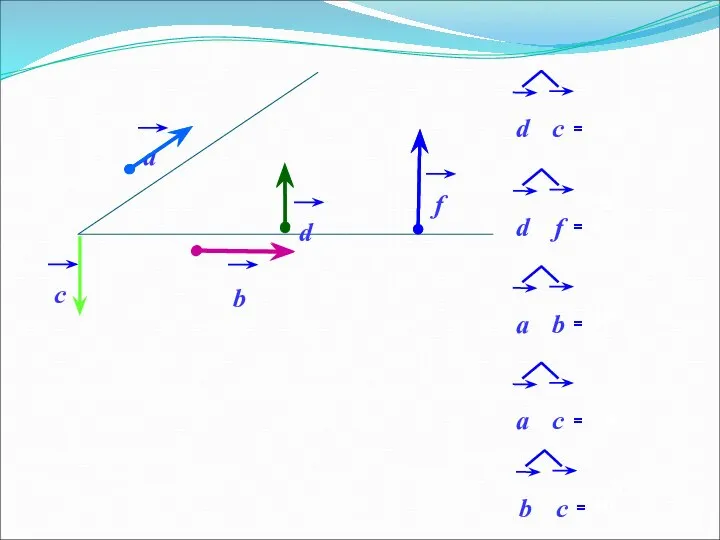
- 9. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
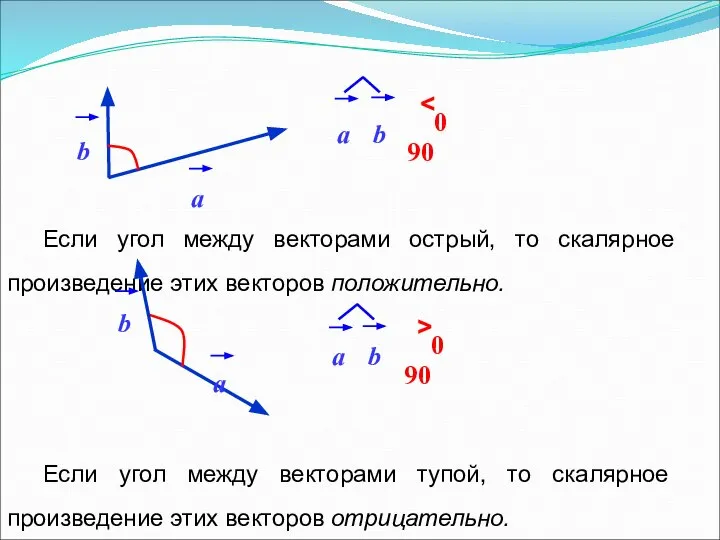
- 10. Если угол между векторами острый, то скалярное произведение этих векторов положительно. Если угол между векторами тупой,
- 12. Скачать презентацию






 Измерение углов. Транспортир
Измерение углов. Транспортир Числовые промежутки. Пересечение и объединение промежутков
Числовые промежутки. Пересечение и объединение промежутков Ортодромия и локсодромия
Ортодромия и локсодромия Тригонометрические функции
Тригонометрические функции Свойства функций. Чтение свойств функций по их графикам
Свойства функций. Чтение свойств функций по их графикам Звёздный час в математике
Звёздный час в математике Дополни до 10
Дополни до 10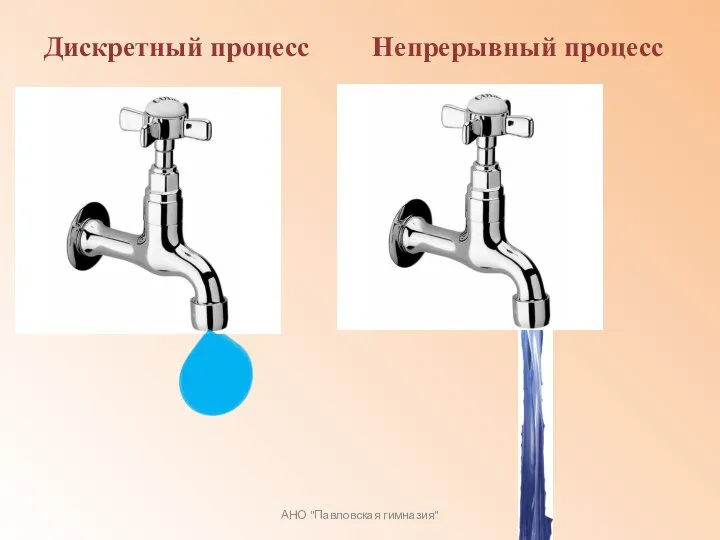 Дискретный процесс. Непрерывный процесс. Производная
Дискретный процесс. Непрерывный процесс. Производная Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата
Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата Обобщающий урок по теме Многогранники
Обобщающий урок по теме Многогранники Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ  Последовательности и прогрессии (ПР №25)
Последовательности и прогрессии (ПР №25) Используется ли в учебниках 7-го класса термин Функциональная зависимость?
Используется ли в учебниках 7-го класса термин Функциональная зависимость? Сокращение дробей. Тождество
Сокращение дробей. Тождество Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Основы системной динамики
Основы системной динамики Исаак Ньютон
Исаак Ньютон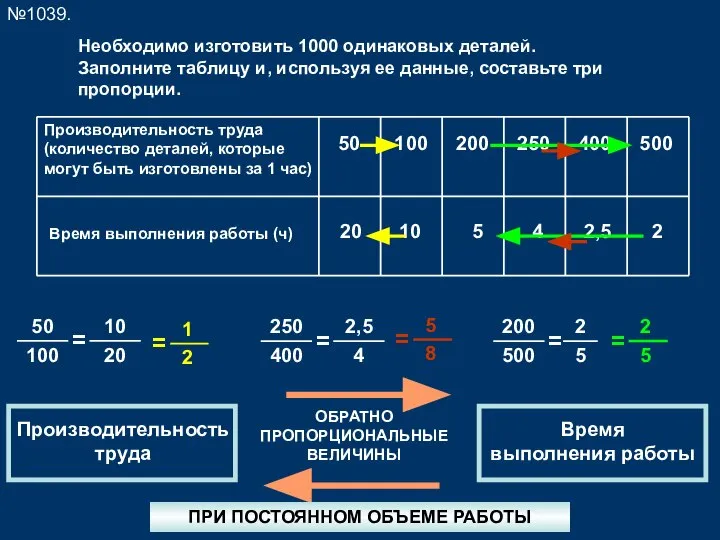 Пропорциональные величины
Пропорциональные величины Random module methods. Test
Random module methods. Test Умножение матрицы на число
Умножение матрицы на число Математическое обеспечение (МО) цифрового (автоматизированного) проектирования
Математическое обеспечение (МО) цифрового (автоматизированного) проектирования Взаимное расположение прямых в пространстве. Угол между двумя прямыми
Взаимное расположение прямых в пространстве. Угол между двумя прямыми Дифференциальные уравнения
Дифференциальные уравнения Нелинейное программирование
Нелинейное программирование Распределительная логистика. Практическое задание №8
Распределительная логистика. Практическое задание №8 Урок математики по теме: Сложение и вычитание в пределах 20
Урок математики по теме: Сложение и вычитание в пределах 20 Решение задач на движение
Решение задач на движение Математический диктант
Математический диктант