Содержание
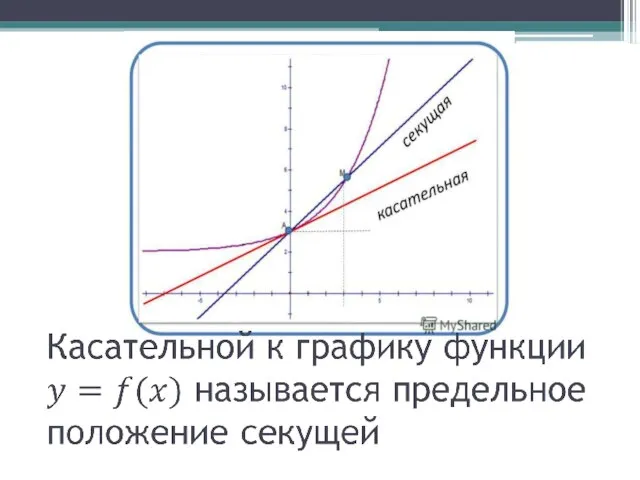
- 2. Цели урока Ввести понятие касательной к графику функции в точке и выяснить в чем состоит геометрический
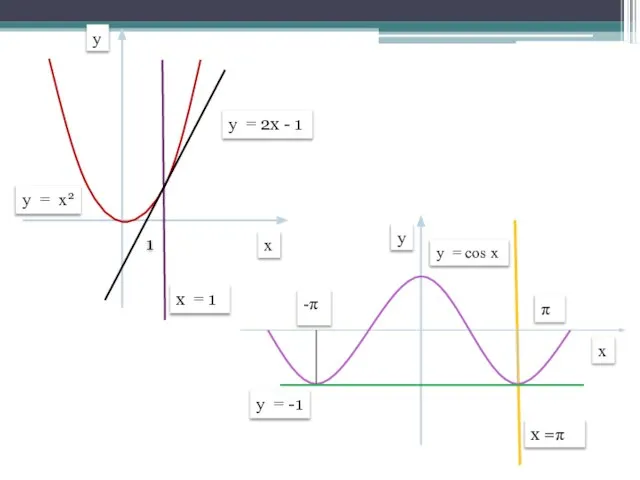
- 5. 1 y = -1 x y y = cos x -π π x y y =
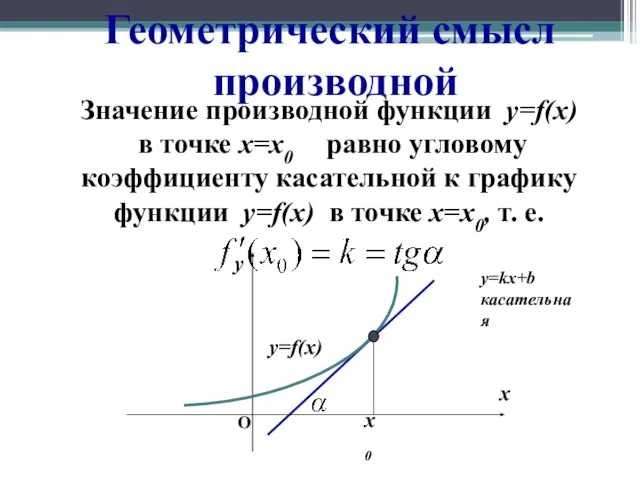
- 6. Геометрический смысл производной Значение производной функции у=f(x) в точке x=x0 равно угловому коэффициенту касательной к графику
- 7. Причем, если : .
- 8. Уравнение касательной
- 9. Алгоритм Найти значение функции в точке хо Вычислить производную функции Найти значение производной функции в точке
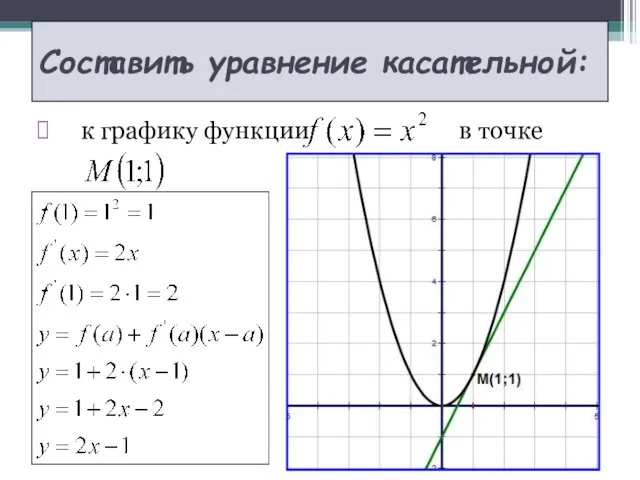
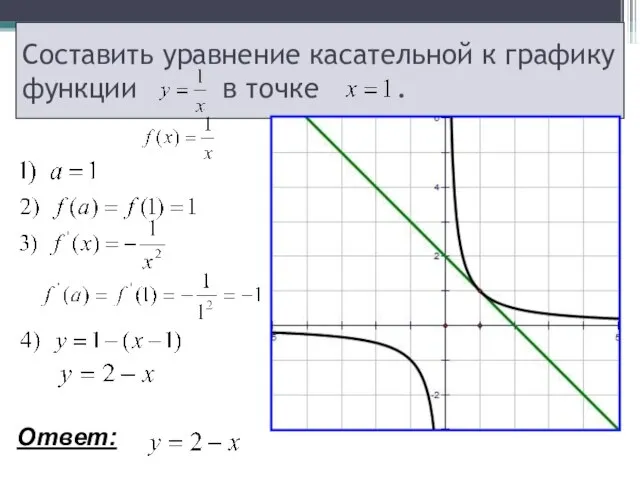
- 10. Составить уравнение касательной: к графику функции в точке
- 11. Составить уравнение касательной к графику функции в точке . Ответ:
- 12. Исследование функции на монотонность
- 13. Исследовать функцию на монотонность – это значит выяснить, на каких промежутках из области определения функция возрастает,
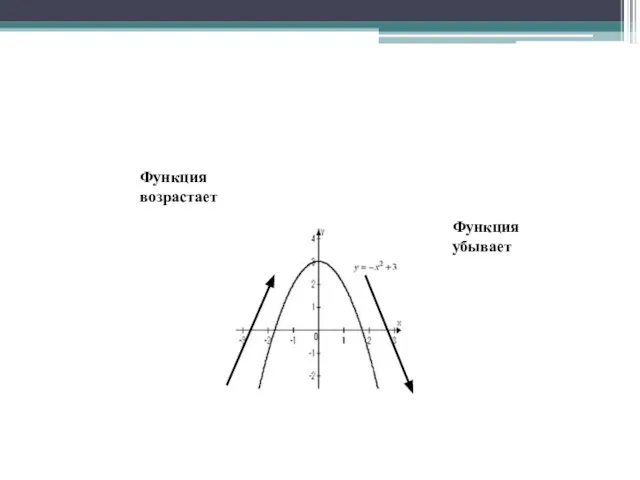
- 14. Функция возрастает Функция убывает
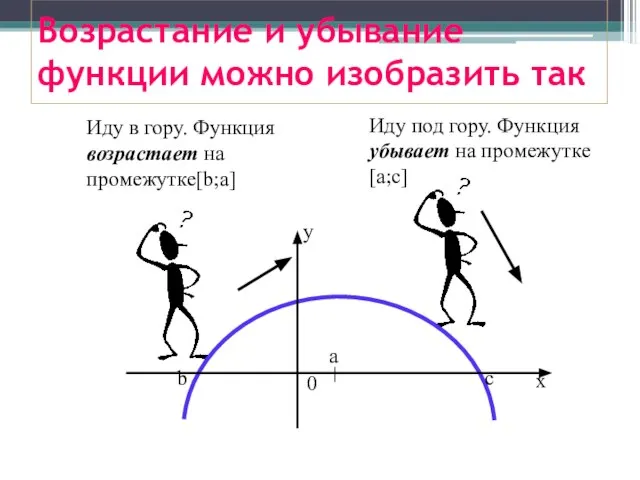
- 15. Возрастание и убывание функции можно изобразить так Иду в гору. Функция возрастает на промежутке[b;a] Иду под
- 16. Для определения промежутков возрастания и убывания функции можно использовать и производную .
- 17. Теорема: Если f(x) – непрерывна на промежутке и имеет f´(x), то а) если f´(x) > 0,
- 18. Алгоритм исследования функции на монотонность Найти производную функции f ΄(х) Найти стационарные (f ΄(х) = 0)
- 19. Определения Внутренние точки области определения функции, в которых производная функции равна нулю, называются стационарными. Внутренние точки
- 20. Например: найти промежутки монотонности функции f(x) = x³ - 6x² + 9x – 1 1) f´(x)
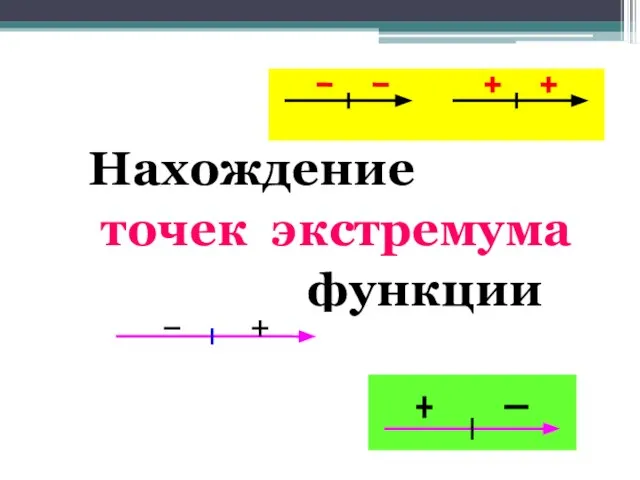
- 21. Нахождение точек экстремума функции
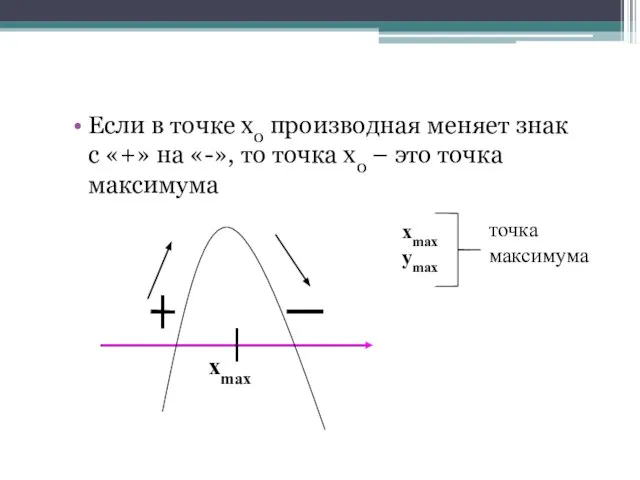
- 22. Если в точке х0 производная меняет знак с «+» на «-», то точка х0 – это
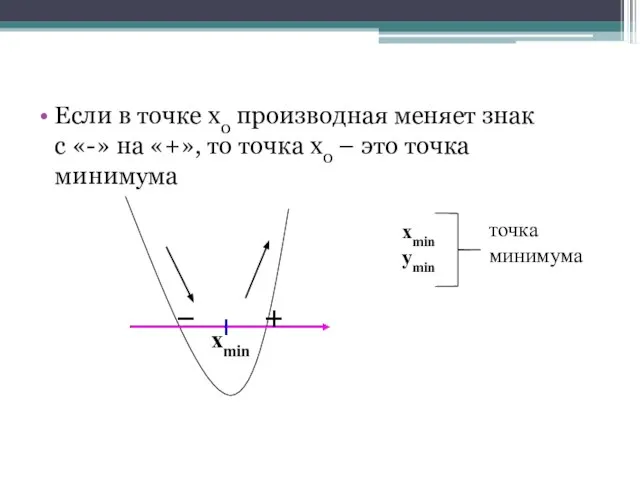
- 23. Если в точке х0 производная меняет знак с «-» на «+», то точка х0 – это
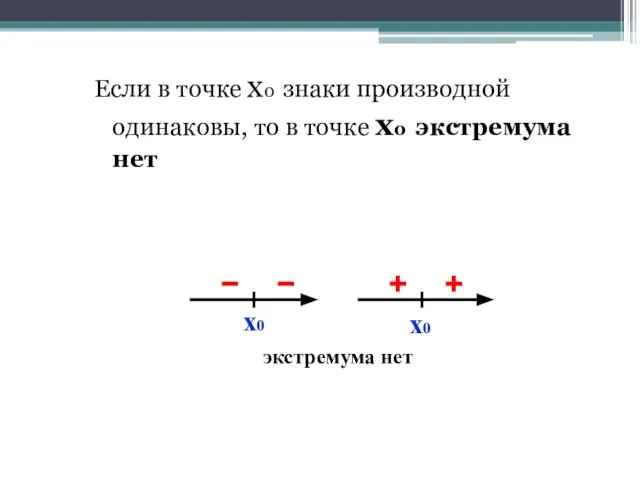
- 24. Если в точке х0 знаки производной одинаковы, то в точке х0 экстремума нет х0 х0 экстремума
- 25. Алгоритм нахождения точек экстремума функции Найти производную функции f ΄(х) Найти стационарные и критические точки функции
- 26. Например: найти точки экстремума функции Решение. 1) у΄=12 х³ - 48х² + 48х = = 12х(х²-4х+4)
- 27. х = 0 – точка минимума, хmin = 0 (0;-11) точка минимума (экстремума)
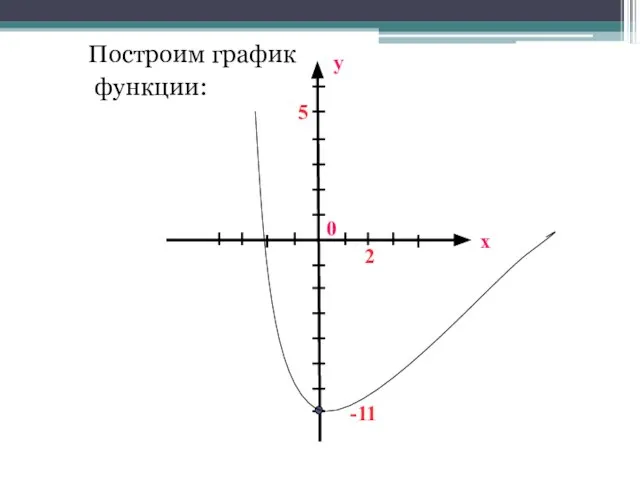
- 28. Построим график функции: х у 0 5 2 -11
- 29. Например: исследовать функцию у = 2х³+3х² -1 и построить её график Решение. D(у)= (-∞; +∞), четность
- 30. Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞) - функция возрастает при
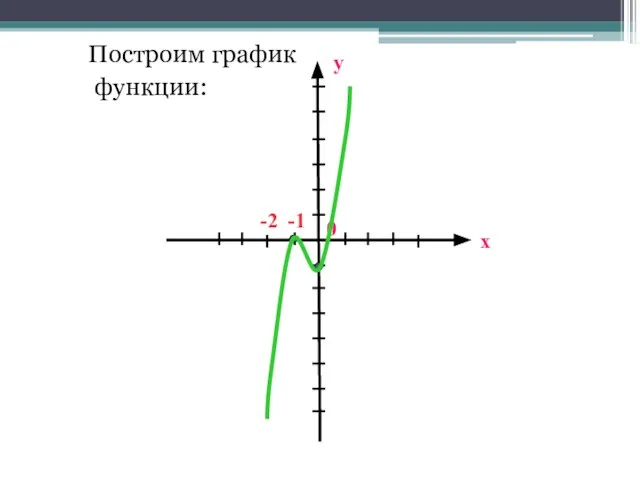
- 31. Построим график функции: х у 0 -1 -2
- 33. Скачать презентацию
















![Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/847663/slide-29.jpg)
 Векторы. Действия с векторами
Векторы. Действия с векторами Брейн-ринг. Математика
Брейн-ринг. Математика Метод наименьших квадратов
Метод наименьших квадратов Свойства корня п- ой степени
Свойства корня п- ой степени Порядок оформления практической работы
Порядок оформления практической работы Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Свойства квадратных корней
Свойства квадратных корней Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД 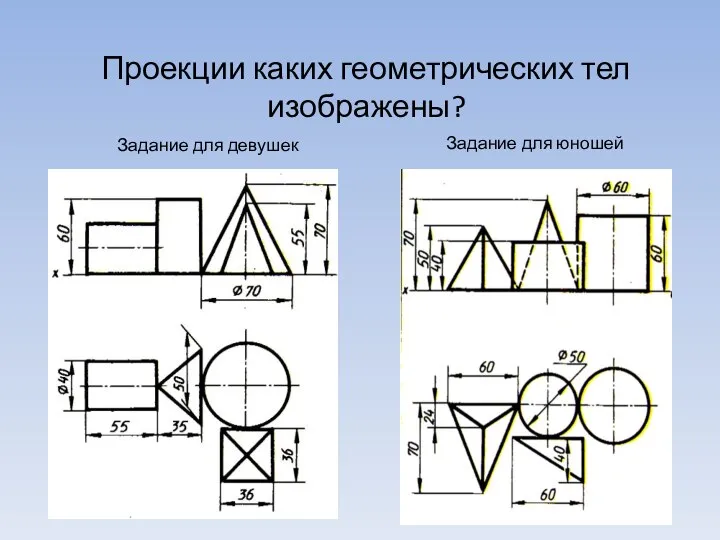 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? У мольберта - математик
У мольберта - математик Векторное исчисление
Векторное исчисление Теорема Гаусса-Остроградского
Теорема Гаусса-Остроградского Таблица значений синуса и тангенса для углов
Таблица значений синуса и тангенса для углов Виды углов
Виды углов Завдання на відсотки
Завдання на відсотки Определение и свойства тройных интегралов
Определение и свойства тройных интегралов Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Макет школи майбутнього виконаний із геометричних тіл
Макет школи майбутнього виконаний із геометричних тіл Простейшие тригонометрические уравнения, содержащие тангенс или котангенс
Простейшие тригонометрические уравнения, содержащие тангенс или котангенс Функции многих переменных
Функции многих переменных Решаем задачу
Решаем задачу Логарифмическая функция
Логарифмическая функция Занимательные задачи на смекалку
Занимательные задачи на смекалку Переменные. Уравнения
Переменные. Уравнения Математика и здоровье
Математика и здоровье Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23
Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23