Содержание
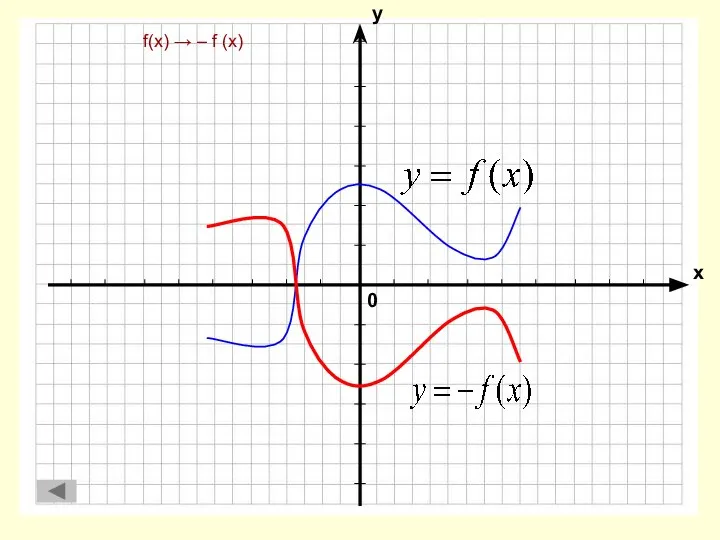
- 2. f(x) → – f (x)
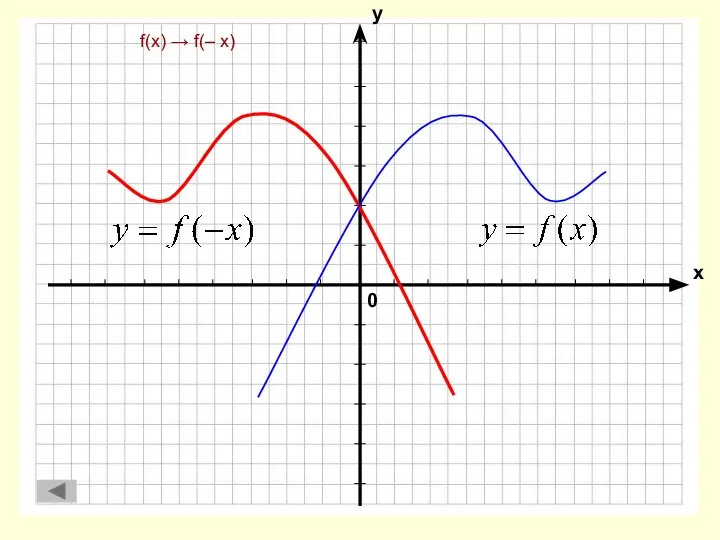
- 3. f(x) → f(– x)
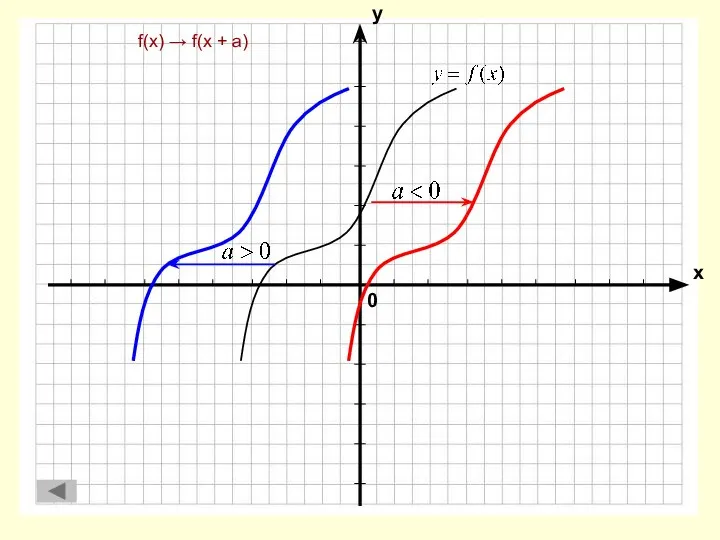
- 4. f(x) → f(x + а)
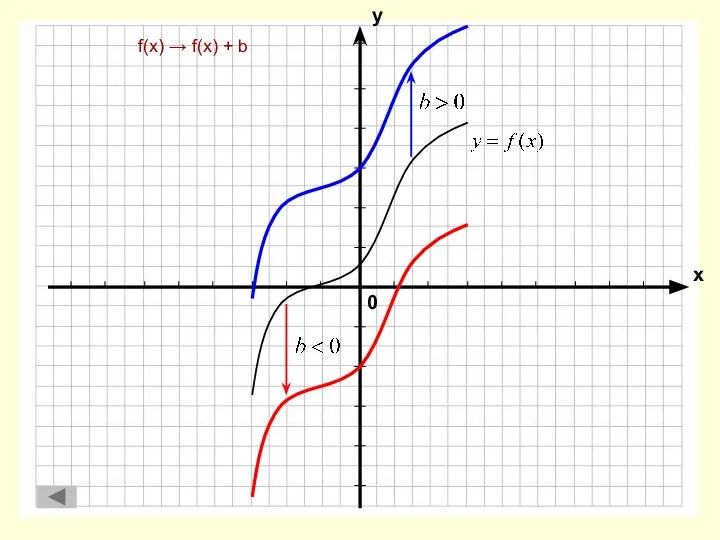
- 5. f(x) → f(x) + b
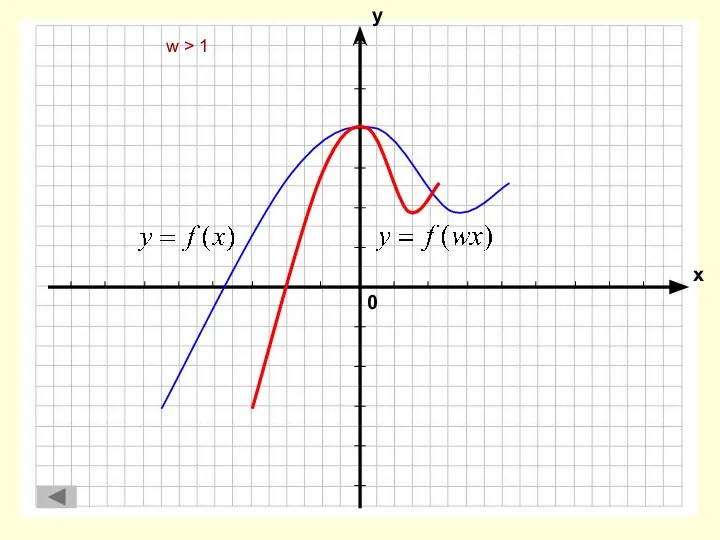
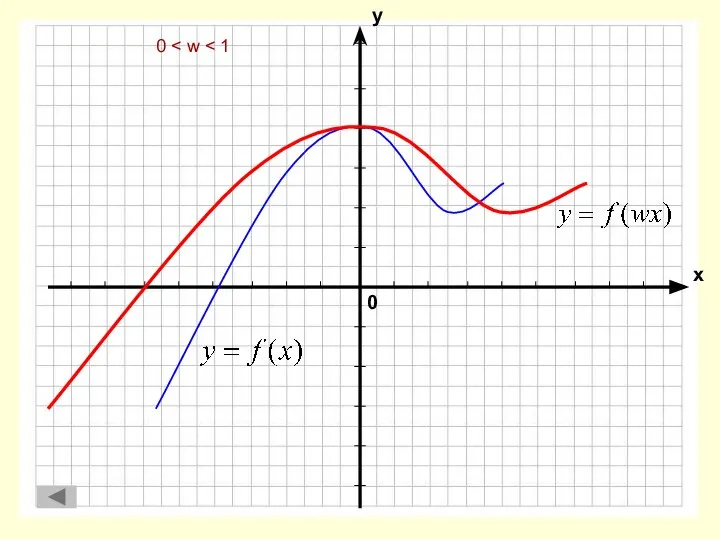
- 6. f(x) → f(wx) 0 w > 1
- 7. w > 1
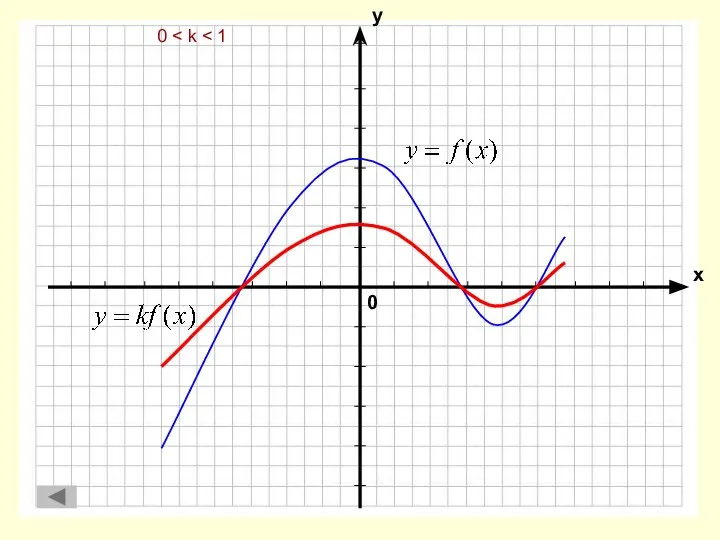
- 8. 0
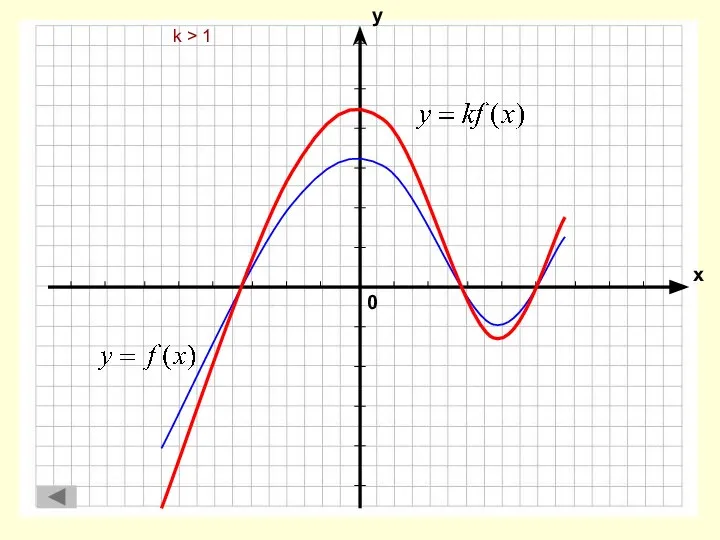
- 9. k > 1 0
- 10. 0
- 11. k > 1
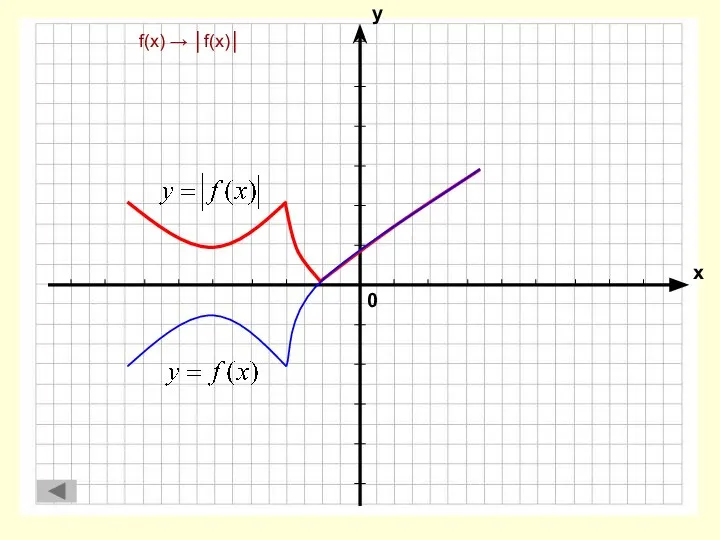
- 12. f(x) → │f(x)│
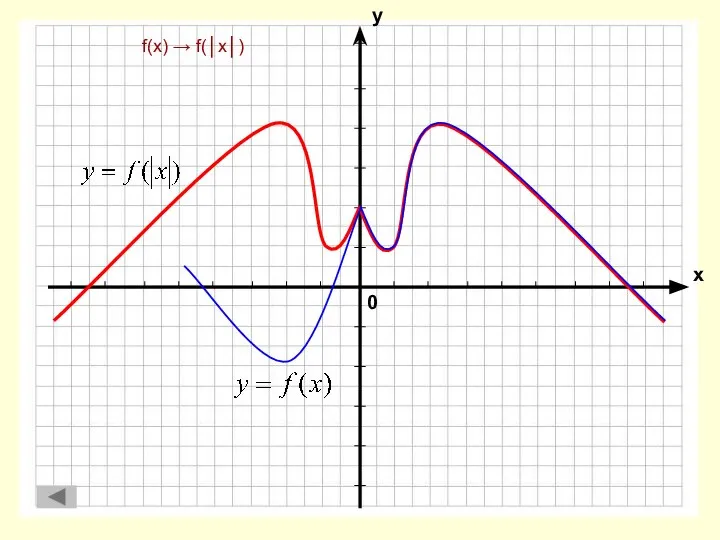
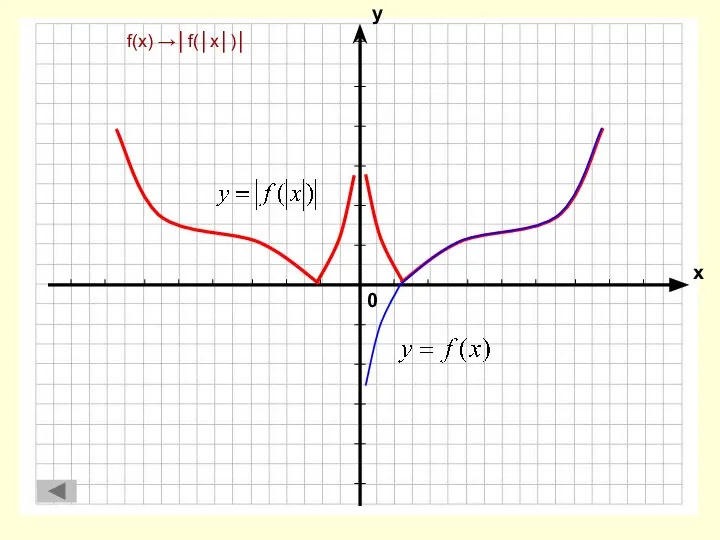
- 13. f(x) → f(│x│)
- 14. f(x) →│f(│x│)│
- 15. последовательныe преобразования графиков элементарных функций (на примерах) Содержание
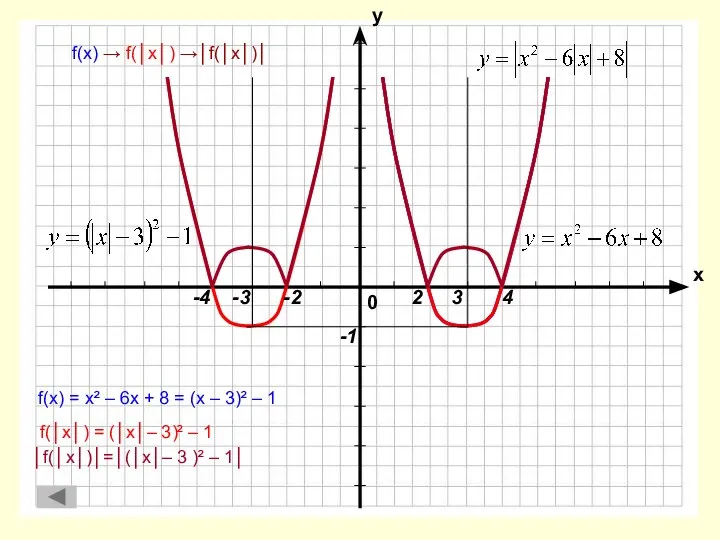
- 16. f(x) → f(│x│) →│f(│x│)│ f(x) = x² – 6x + 8 = (x – 3)² –
- 17. f(x) = x² – 6x + 8 = (x – 3)² – 1 f(│x│) = (│x│–
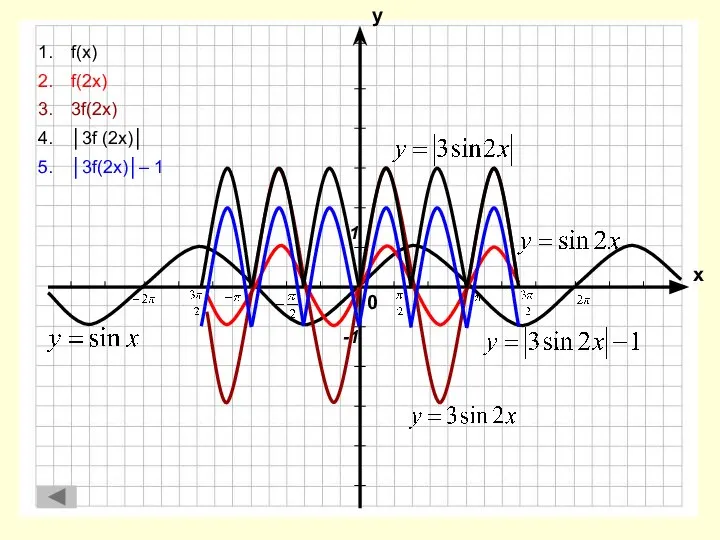
- 18. f(x) f(2x) 3f(2x) │3f (2x)│ │3f(2x)│– 1 1 -1
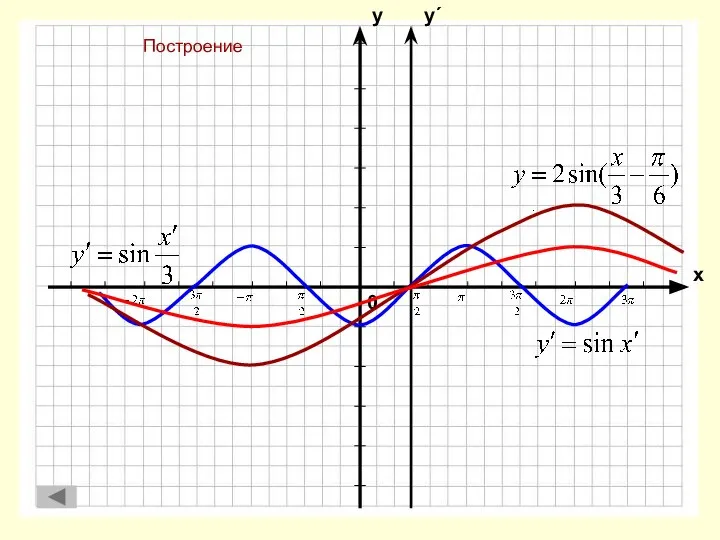
- 20. Построение у΄
- 21. Проверь себя Содержание
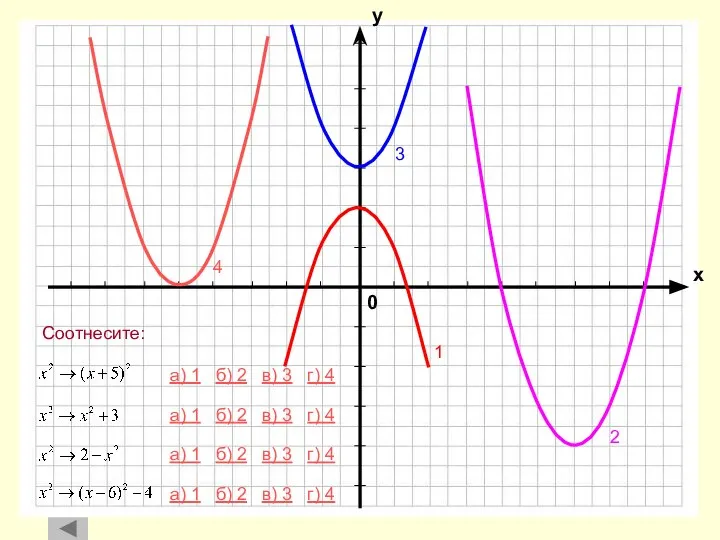
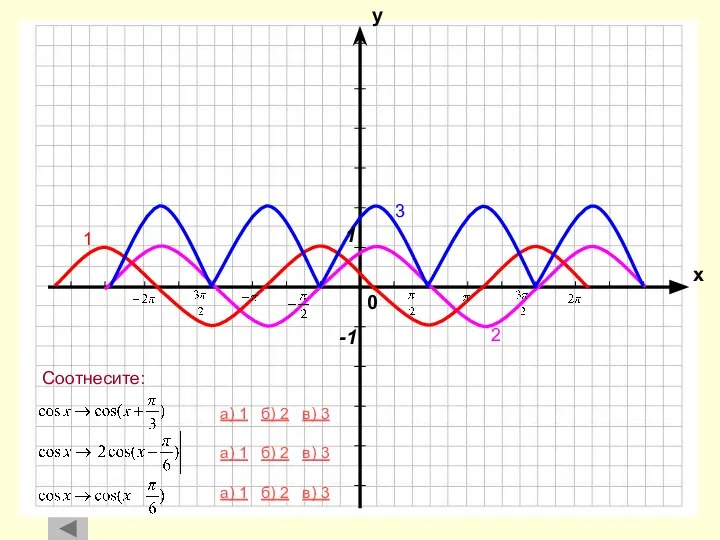
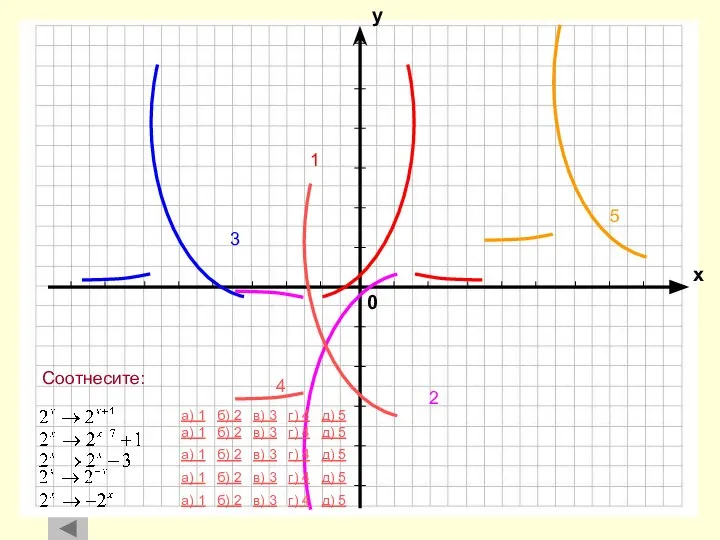
- 22. 4 1 2 3 а) 1 б) 2 в) 3 г) 4 а) 1 б) 2
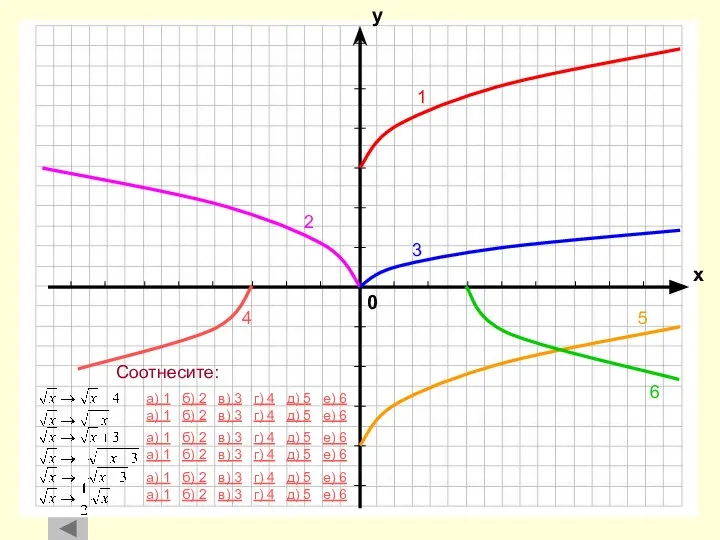
- 23. а) 1 б) 2 в) 3 г) 4 д) 5 е) 6 4 1 2 3
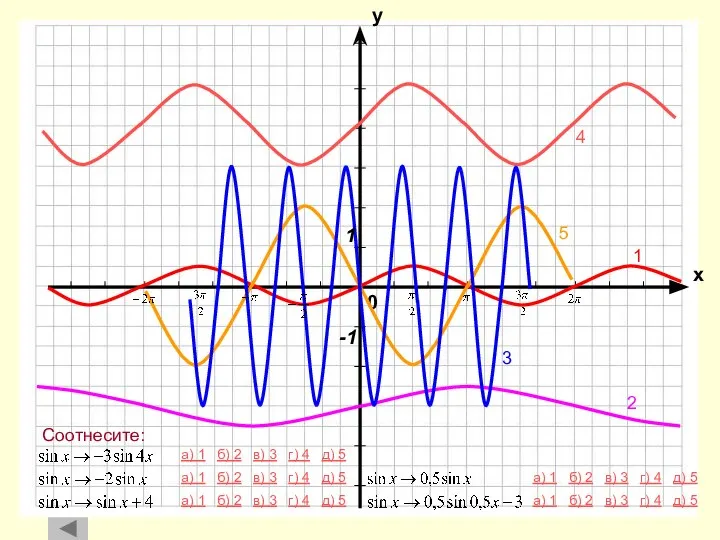
- 24. а) 1 б) 2 в) 3 г) 4 д) 5 а) 1 б) 2 в) 3
- 25. а) 1 б) 2 в) 3 а) 1 б) 2 в) 3 а) 1 б) 2
- 26. 4 1 2 3 5 а) 1 б) 2 в) 3 г) 4 д) 5 а)
- 27. Всё!
- 28. Молодец!
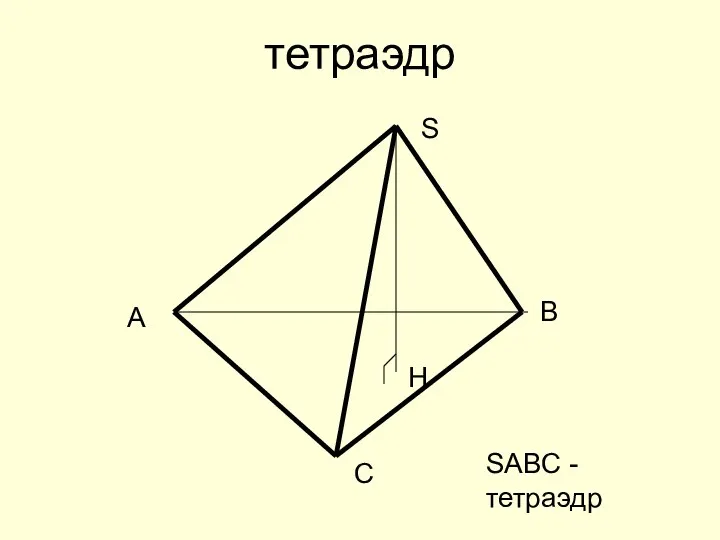
- 29. тетраэдр A B C S H SABC - тетраэдр
- 30. Кластер Основание; Ребра; Вершины; Грани; Высоты.
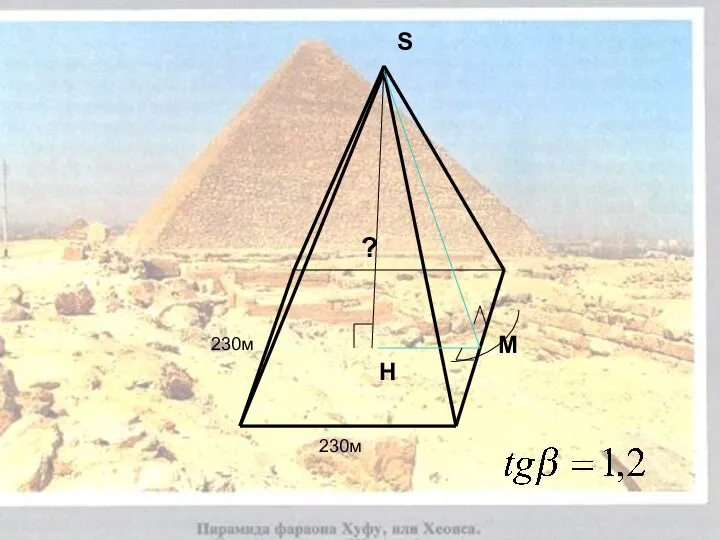
- 31. На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса
- 32. Центральная Америка к северу от Мехико город Теотиукан Пирамида Солнца
- 33. остров Тенериф: Пирамиды Гуимар
- 34. На фоне Гималайского хребта четко выделяется пирамидальное образование – гора Кайлас
- 35. Стеклянная пирамида в Париже Новый вход в Лувр, высота 21,65метра
- 36. Франкфурт: загородный дом 1896 года. Одна из башен имеет форму пирамиды и придает зданию величавый вид.
- 37. Алгоритм Определение. Основание. Боковая грань Вершины. Ребра. Площадь боковой поверхности. Площадь полной поверхности
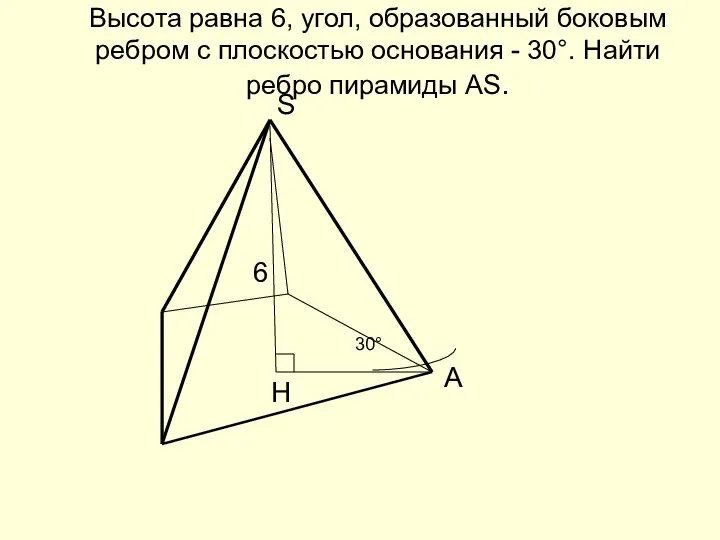
- 38. Высота равна 6, угол, образованный боковым ребром с плоскостью основания - 30°. Найти ребро пирамиды AS.
- 39. 230м 230м 230м ? S H M
- 40. Тест : Сколько граней, боковых ребер у n-угольной пирамиды? Какое наименьшее число граней может иметь пирамида?
- 42. Скачать презентацию
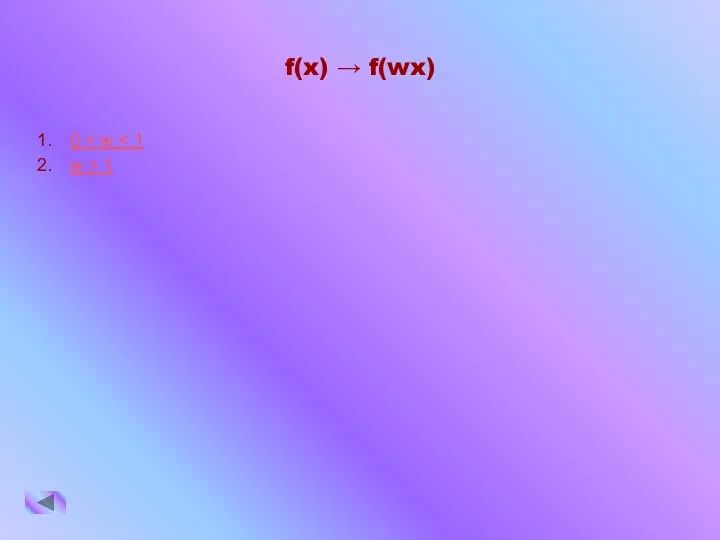
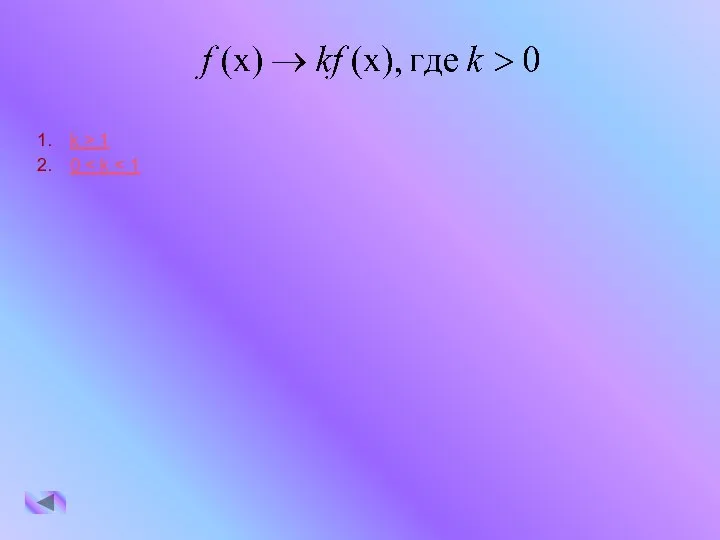



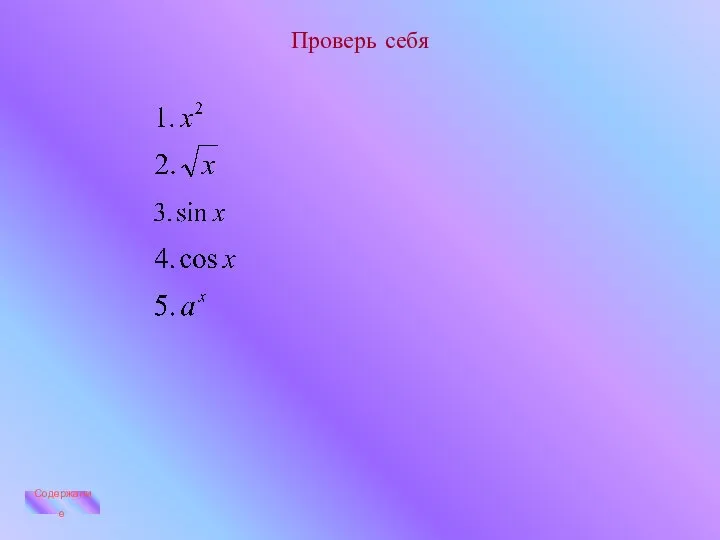











 Прямоугольник
Прямоугольник Как лгать при помоощи статистики
Как лгать при помоощи статистики Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Координатная плоскость
Координатная плоскость Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Построение и анализ параллельных алгоритмов
Построение и анализ параллельных алгоритмов Симметрия. Виды симметрии
Симметрия. Виды симметрии Графики тригонометрических функций
Графики тригонометрических функций ГИА - 2018. Открытый банк заданий по математике. Задача №12
ГИА - 2018. Открытый банк заданий по математике. Задача №12 Тренажер вычисления производной
Тренажер вычисления производной Правильные многогранники
Правильные многогранники Массивы. Работа с массивами
Массивы. Работа с массивами Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Однородные тригонометрические уравнения
Однородные тригонометрические уравнения 13_razn_dejstv_1
13_razn_dejstv_1 Сложение с переходом через десяток вида +8, +9. Считаем с гномами
Сложение с переходом через десяток вида +8, +9. Считаем с гномами Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА
Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА  Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками
Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Преобразование графиков квадратичной функции. 8 класс
Преобразование графиков квадратичной функции. 8 класс Таблица умножения. Анимированная сорбонка
Таблица умножения. Анимированная сорбонка Решение геометрических задач. Треугольники
Решение геометрических задач. Треугольники Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Свойства сложения
Свойства сложения Случаи вычитания 14 -
Случаи вычитания 14 - Площадь треугольника
Площадь треугольника