Содержание
- 2. Перепишем систему уравнений в матричной форме: Так как то систему трёх линейных уравнений с тремя неизвестными
- 3. Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы : где
- 4. Осталось вычислить матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов: Ответ: .
- 6. Скачать презентацию



 Сказ о дележе наследства (задача)
Сказ о дележе наследства (задача) Вычисление статистических характеристик случайных величин
Вычисление статистических характеристик случайных величин Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  Вычитание чисел с переходом через разряд. Проверочная работа. 1 класс
Вычитание чисел с переходом через разряд. Проверочная работа. 1 класс Диаграммы
Диаграммы Контрольная работа
Контрольная работа Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер Урок геометрии в 8 классе по теме Площадь
Урок геометрии в 8 классе по теме Площадь Основные физические константы. Основные математические константы
Основные физические константы. Основные математические константы Площадь параллелограмма. 8 класс
Площадь параллелограмма. 8 класс Презентация на тему Производная сложной функции
Презентация на тему Производная сложной функции  Марафон по математике. Задание 13
Марафон по математике. Задание 13 Новогодняя сказка в Стране математики. Для детей 5-ти лет
Новогодняя сказка в Стране математики. Для детей 5-ти лет Геометрические фигуры (круг)
Геометрические фигуры (круг) Сложение и вычитание чисел с переходом через десяток
Сложение и вычитание чисел с переходом через десяток Математика. Разминка
Математика. Разминка Пропорции и отношения. Тест
Пропорции и отношения. Тест Статистическая проверка гипотез
Статистическая проверка гипотез Мастер-класс в рамках игры физико-математические забавы
Мастер-класс в рамках игры физико-математические забавы Построение сечений многогранников
Построение сечений многогранников Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата
Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н.
УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н.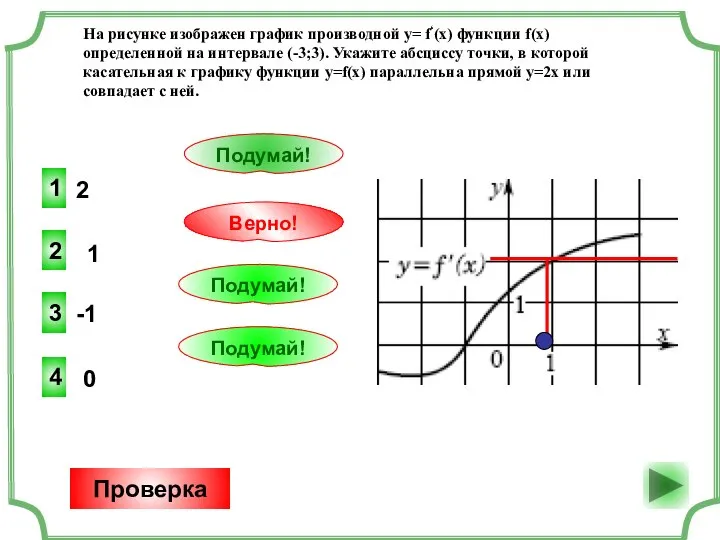 Решение задач
Решение задач Решение квадратного уравнения общего вида
Решение квадратного уравнения общего вида Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Число семь. Цифра 7
Число семь. Цифра 7 Вписанная окружность
Вписанная окружность Цифры
Цифры