Призма

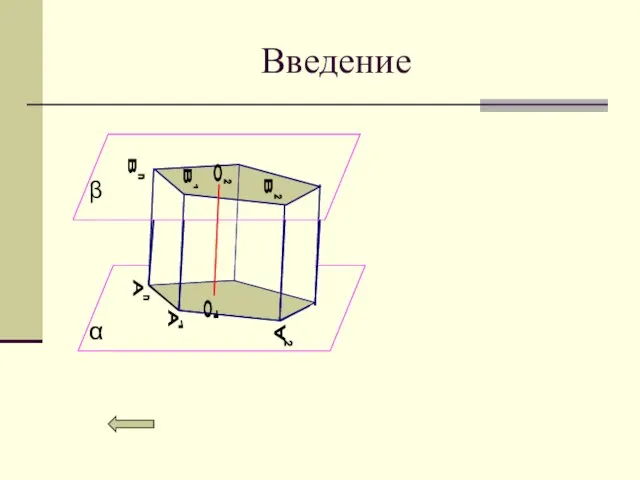
Введение
Рассмотрим два равных многоугольника A1A2…An и B1B2…Bn , расположенных в параллельных плоскостях α и β так, что отрезки A1B1 ,A2B2, …,AnBn, соединяющие соответственные вершины многоугольников, параллельны.
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn , расположенных в параллельных плоскостях, и n параллелограммов (1), называется призмой.

Введение
A
A
1
2
A
n
2
1
n
B
B
B
O
O
1
2
α
β

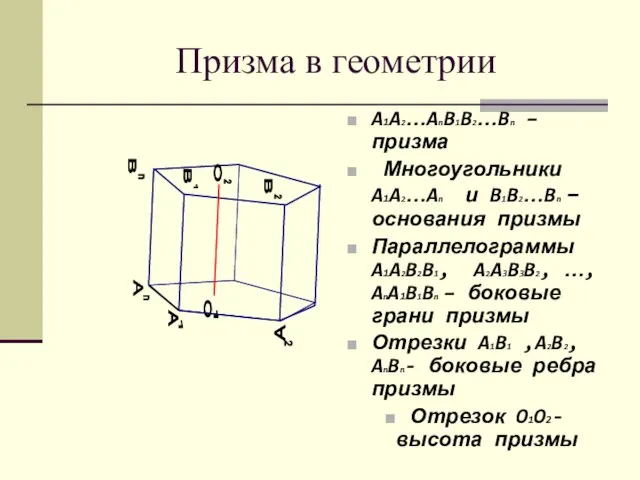
Призма в геометрии
Призма — многогранник, который состоит из двух плоских равных многоугольников с соответственно параллельными сторонами и отрезков, соединяющих соответствующие точки этих многоугольников.
Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, — боковыми рёбрами призмы. Все боковые грани призмы – параллелограммы.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой.

Призма в геометрии
A
A1A2…AnB1B2…Bn – призма
Многоугольники A1A2…An и B1B2…Bn – основания призмы
Параллелограммы A1A2B2B1, A2A3B3B2, …, AnA1B1Bn – боковые грани призмы
Отрезки A1B1 ,A2B2, AnBn- боковые ребра призмы
Отрезок O1O2- высота призмы
A
1
2
A
n
2
1
n
B
B
B
O
O
1
2

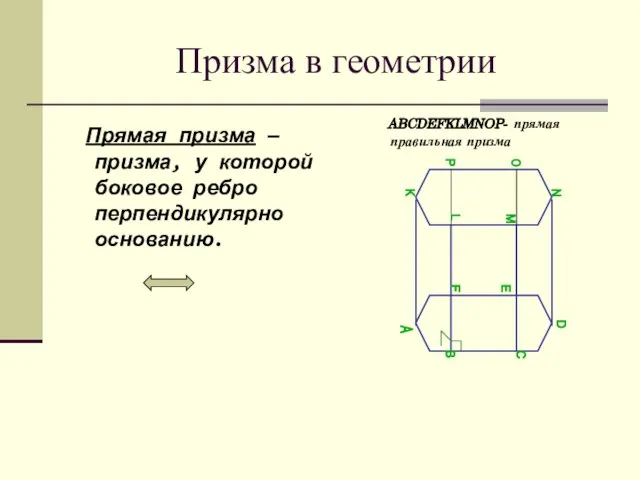
Призма в геометрии
Прямая призма — призма, у которой боковое ребро перпендикулярно основанию. ABCDEFKLMNOP- прямая правильная призма
A
B
C
D
K
L
M
N
E
O
F
P

Призма в геометрии
Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой.
Боковое ребро прямой призмы, в том числе и правильной, есть ее высота. Отрезок, концы которого - две вершины, не принадлежащие одной грани призмы, называют ее диагональю. Сечение призмы с плоскостью, проходящей через два боковых ребра, не лежащих в одной грани, называют диагональным сечением призмы.

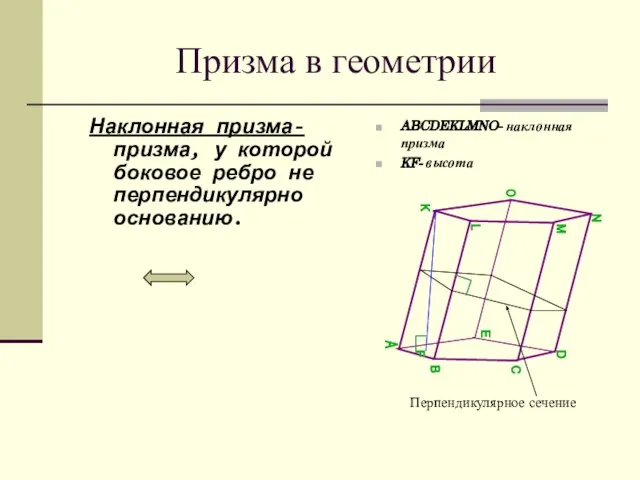
Призма в геометрии
Наклонная призма- призма, у которой боковое ребро не перпендикулярно основанию.
ABCDEKLMNO- наклонная призма
KF- высота
Перпендикулярное сечение
A
B
C
D
K
L
M
N
E
O
F

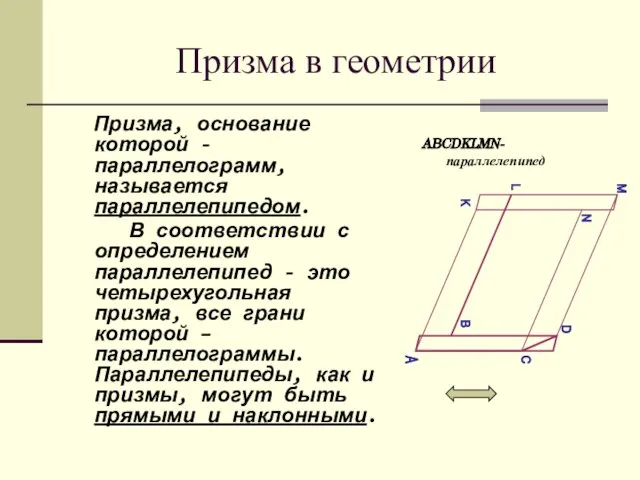
Призма в геометрии
Призма, основание которой - параллелограмм, называется параллелепипедом.
В соответствии с определением параллелепипед - это четырехугольная призма, все грани которой – параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
ABCDKLMN- параллелепипед
A
B
C
D
K
L
M
N

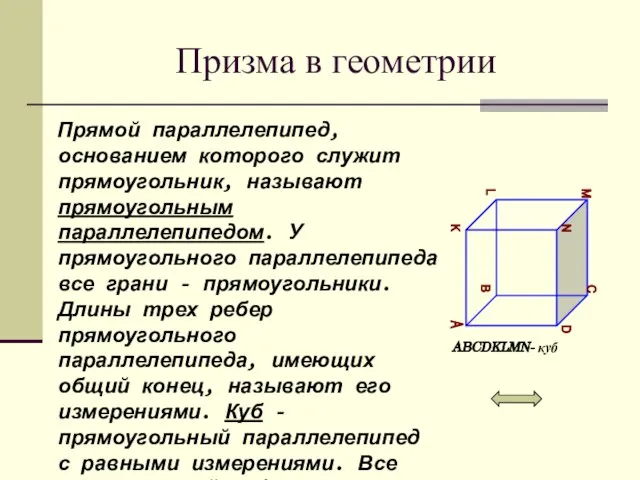
Призма в геометрии
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани - прямоугольники.
Длины трех ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Куб - прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.
ABCDKLMN- куб
A
B
C
D
K
L
M
N

Призма в геометрии
Призма:
Sбок=P l
Sполн=2Sо+Sбок
V=Sоl
Прямая призма: Sбок=Pоl(l=h)
Параллелепипед:
Sполн=2(ab+bc+ac)
V=abc
d²=a²+b²+c²
Куб:
Sполн=6a²
V=a³
d²=3a²
Обозначения:
V- объем;
Sполн- площадь полной поверхности;
Sбок- площадь боковой поверхности;
Sо- площадь основания;
Pо- периметр основания;
P - периметр перпендикулярного сечения;
l- длина ребра;
h- высота.

Теоремы
Объем прямой призмы равен произведению площади основания на высоту.
Объем наклонной призмы равен произведению площади основания на высоту.
Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

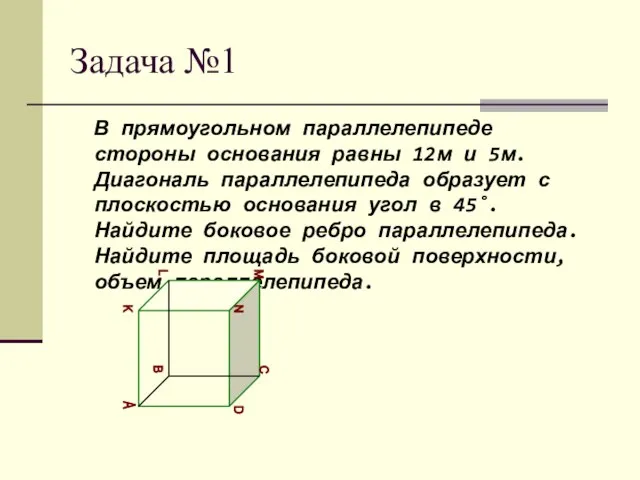
Задача №1
В прямоугольном параллелепипеде стороны основания равны 12м и 5м. Диагональ параллелепипеда образует с плоскостью основания угол в 45˚. Найдите боковое ребро параллелепипеда. Найдите площадь боковой поверхности, объем параллелепипеда.
A
B
C
D
K
L
M
N

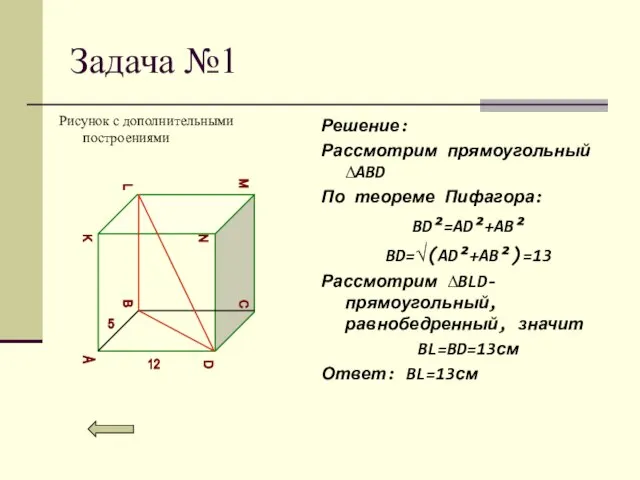
Задача №1
Рисунок с дополнительными построениями
Решение:
Рассмотрим прямоугольный ∆ABD
По теореме Пифагора:
BD²=AD²+AB²
BD=√(AD²+AB²)=13
Рассмотрим ∆BLD-прямоугольный, равнобедренный, значит
BL=BD=13см
Ответ: BL=13см
A
K
B
C
D
L
M
N
12
5

Задача №2
Высота прямой треугольной призмы ABCA1B2C3 равна 10. Расстояние от вершины A до плоскости A1BC равно 6. Найдите площадь сечения призмы плоскостью A1BC, если BC равен 16.

Задача №2
Рисунок с дополнительными построениями
Решение:
Сечение A1BC разбивает призму ABCA1B1C1 на две пирамиды AA1BC иA1BB1C1C. Пусть V– объем призмы, V1- объем пирамиды AA1BC1, V2 - объем пирамиды A1BB1C1C. По свойству V=V1+V2 (1)
Проведем AM перпендикулярную BC, тогда A1M перпендикулярен BC. Обозначим AM=h, A1M=√100+h². Проведем MM1 AA1, тогда AM перпендикулярен MM1, значит AM перпендикулярен BB1C1, A1M1 AM → A1M1 перпендикулярен BB1C, A1M1=AM=h
M
M
1

Задача №2
Найдем V, V1, V2.
V=SABC•AA1=½•16•h•10=80h
V1=⅓•SA1BC•AE= =⅓•½•16•(√100+h²)•6=16•(√100+h²)
V2=⅓•SBB1C1C•A1M1=⅔•16•h•10=160/3h
Найденные значения подставим в формулу(1):
80h=16•(√100+h²)+160/3h
h=7,5
SABC=½•BC•A1M=½•16•(√100+56,25)=100
Ответ: S=100

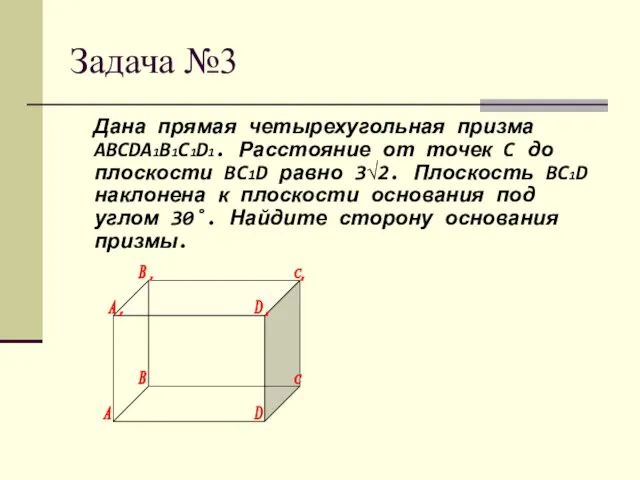
Задача №3
Дана прямая четырехугольная призма ABCDA1B1C1D1. Расстояние от точек C до плоскости BC1D равно 3√2. Плоскость BC1D наклонена к плоскости основания под углом 30˚. Найдите сторону основания призмы.
A
A
B
B
C
C
D
D
1
1
1
1

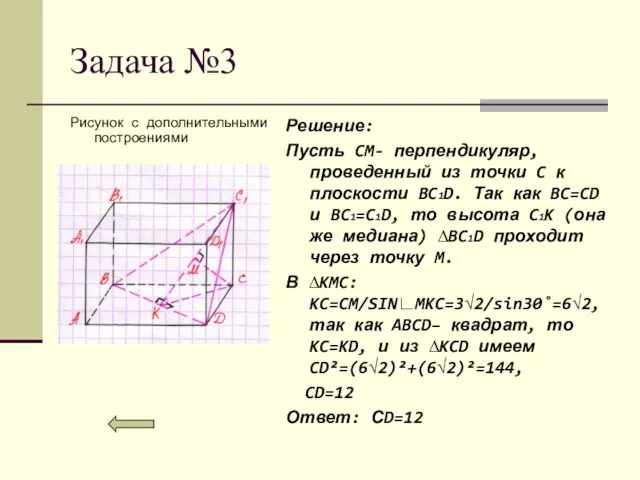
Задача №3
Решение:
Пусть CM- перпендикуляр, проведенный из точки C к плоскости BC1D. Так как BC=CD и BC1=C1D, то высота C1K (она же медиана) ∆BC1D проходит через точку M.
В ∆KMC: KC=CM/SIN∟MKC=3√2/sin30˚=6√2, так как ABCD– квадрат, то KC=KD, и из ∆KCD имеем CD²=(6√2)²+(6√2)²=144,
CD=12
Ответ: СD=12
Рисунок с дополнительными построениями

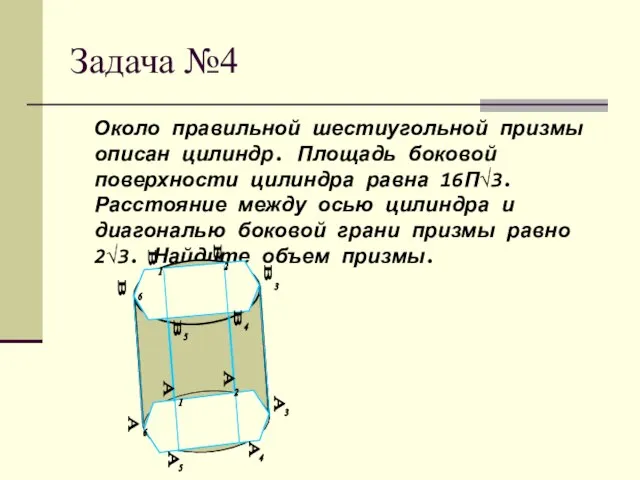
Задача №4
Около правильной шестиугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16П√3. Расстояние между осью цилиндра и диагональю боковой грани призмы равно 2√3. Найдите объем призмы.
A
B
A
A
A
A
A
B
B
B
B
B
3
1
2
2
3
4
4
1
5
5
6
6