Признаки подобия треугольников

11. 04. 19
Классная работа
Признаки подобия треугольников

Мы докажем два признака подобия треугольников. Доказанные ра­нее признаки равенства треугольников являются частными случая­ми признаков подобия треугольников.

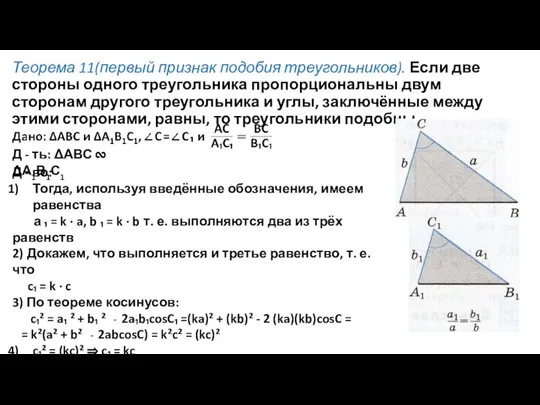
Теорема 11(первый признак подобия треугольников). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
Д - ть: ΔАВС ∾ ΔА1В1С1
Д - во:
Тогда, используя введённые обозначения, имеем равенства
а ₁ = k · a, b ₁ = k · b т. е. выполняются два из трёх равенств
2) До­кажем, что выполняется и третье равенство, т. е. что
c₁ = k · c
3) По теореме косинусов:
c₁² = a₁ ² + b₁ ² - 2a₁b₁cosC₁ =(ka)² + (kb)² - 2 (ka)(kb)cosC =
= k²(a² + b² - 2abcosC) = k²c² = (kc)²
c₁² = (kc)² ⇒ c₁ = kc
а ₁ = ka, b ₁ = kb, c₁ = kc - все три пары сторон рассматриваемых треугольников пропор­циональны и эти треугольники подобны.

Теорема 12(второй признак подобия тре­угольников). Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Дано: ΔАВС и ΔА1В1С1, ∠A =∠A₁ и ∠B =∠B₁
Д - ть: ΔАВС ∾ ΔА1В1С1

Замечание.
Отметим, что первый признак подобия треугольников вытекает из теоремы ко­синусов, а второй — из теоремы синусов.

Дополняем теорию
9. 12
Хорда треугольника, параллельная его стороне, отсекает от не­го треугольник, подобный данному. Докажите. Проверьте об­ратное. Какие следствия вы можете получить из доказанного утверждения?
9. 13
Пусть две параллельные прямые пересекаются тремя (или бо­лее) прямыми, проходящими через одну и ту же точку, не ле­жащую на данных параллельных прямых. Докажите, что на параллельных прямых получились пропорциональные отрезки.

Рассуждаем
9.14. Два угла одного треугольника равны 70° и 80°, а два угла другого треугольника равны 30° и 80°. Подобны ли эти треугольники?
9.15. Какие признаки подобия прямоугольных и равнобедренных треугольников можно получить как непосредственные следствия двух признаков подобия треугольников? А какие уже известные вам признаки подобия прямоугольных и равнобедренных треугольников не являются следствиями общих признаков подобия треугольников?

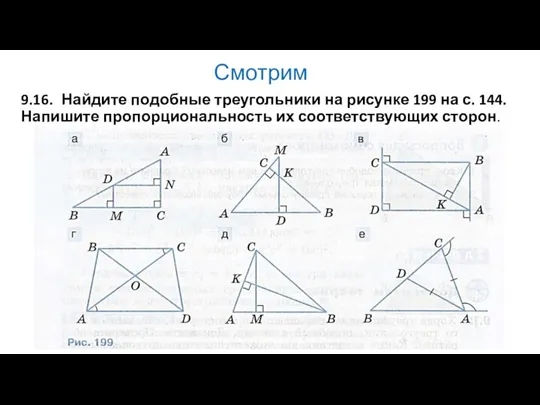
Смотрим
9.16. Найдите подобные треугольники на рисунке 199 на с. 144. Напишите пропорциональность их соответствующих сторон.

9.17. Проведите две медианы треугольника и среднюю линию этого треугольника, соединяющую концы медиан. Найдите на полученном рисунке подобные треугольники. Запишите пропорциональность их соответствующих сторон.

Вычисляем
9.19.
Хорда КМ треугольника АВС идёт из точки К стороны АВ параллельно его стороне ВС. Найдите:
а) ВК, если АК = 4, АМ = 6, МС = 10;
б) МС, если АМ = 2, АВ = 6, АК = 4;
в) АС, если КВ = 3, МС = 4, АВ = 10;
г) КМ, если АК = 4, ВК = 6, БС = 20;
д) ВС, если КМ = 5, АМ = 2, МС = 6.