- Главная
- Математика
- Вычислительная сложность алгоритма

Содержание
- 2. Вычислительная сложность алгоритма Евклида изучена полностью.[17] Эта сложность может быть описана произведением количества шагов деления, требуемых
- 3. КОЛИЧЕСТВО ШАГОВ Число шагов для вычисления НОД двух натуральных чисел a и b обозначим как T(a,
- 4. НАИХУДШИЙ СЛУЧАЙ Если для алгоритма Евклида требуются N шагов для пары натуральных чисел a > b
- 5. ТЕОРЕМА ЛАМЕ Число делений с остатком в процессе применения алгоритма Евклида не превосходит упятеренного количества цифр
- 6. СРЕДНЕЕ Существуют различные способы вычисления среднего количества шагов алгоритма. Первый способ вычисления — среднее время T(a),
- 8. Скачать презентацию
Слайд 2Вычислительная сложность алгоритма Евклида изучена полностью.[17] Эта сложность может быть описана произведением
Вычислительная сложность алгоритма Евклида изучена полностью.[17] Эта сложность может быть описана произведением
![Вычислительная сложность алгоритма Евклида изучена полностью.[17] Эта сложность может быть описана произведением](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/921836/slide-1.jpg)
количества шагов деления, требуемых алгоритмом, на вычислительную сложность одного шага. Первый известный анализ алгоритма Евклида был предложен Рейнаудом в 1811.[18] Он показал, что число шагов алгоритма для пары чисел (u, v) ограничено v. Позже он улучшил оценку до v/2 + 2. Эмиль Леже, в 1837 году, изучил наихудший случай, когда для вычисления НОД подаются последовательные числа Фибоначчи.[19] Затем, в 1841 году, Пьер Джосеф Финк показал,[20] что количество шагов алгоритма не превышает 2 log2 v + 1. Следовательно алгоритм работает за полиномиальное время от размера меньшего из пары чисел (u, v).[19] Анализ Финка был уточнён Габриэлем Ламе в 1844 году.[21] Он показал, что количество шагов, необходимых для завершения алгоритма, не более чем в пять раз превышает h — количество цифр в десятичном представлении меньшего из пары чисел (u, v).[22][23]
Когда НОД вычисляется для чисел, которые вписываются в одно машинное слово, каждый шаг алгоритма занимает постоянное время. В данном случае анализ Ламе предполагает, что вычислительная сложность оценивается как O(h). Однако в модели расчёта, подходящей для вычислений с числами больше одного машинного слова, оценка сложности вычисления одного остатка может быть O(h2).[24] В этом случае общее время для всех этапов алгоритма можно проанализировать с помощью телескопического ряда, показав что это также O(h2). Для ускорения алгоритма Евклида могут быть использованы современные алгоритмические методы, основанные на методе Шёнхаге — Штрассена для быстрого целочисленного умножения . Это приводит к квазиполиномиальному времени.[25]
Когда НОД вычисляется для чисел, которые вписываются в одно машинное слово, каждый шаг алгоритма занимает постоянное время. В данном случае анализ Ламе предполагает, что вычислительная сложность оценивается как O(h). Однако в модели расчёта, подходящей для вычислений с числами больше одного машинного слова, оценка сложности вычисления одного остатка может быть O(h2).[24] В этом случае общее время для всех этапов алгоритма можно проанализировать с помощью телескопического ряда, показав что это также O(h2). Для ускорения алгоритма Евклида могут быть использованы современные алгоритмические методы, основанные на методе Шёнхаге — Штрассена для быстрого целочисленного умножения . Это приводит к квазиполиномиальному времени.[25]
Слайд 3КОЛИЧЕСТВО ШАГОВ
Число шагов для вычисления НОД двух натуральных чисел a и b
КОЛИЧЕСТВО ШАГОВ
Число шагов для вычисления НОД двух натуральных чисел a и b

обозначим как T(a, b). Если g — это наибольший общий делитель a и b, тогда a = mg и b = ng для двух взаимно простых чисел m и n. Тогда T(a, b) = T(m, n), что можно заметить, если разделить уравнения, полученные при вычислении НОД для пары (a, b), на g.[26] Используя тот же принцип, число шагов алгоритма остаётся неизменным, если a и b умножаются на общий множитель w, что эквивалентно равенству T(a, b) = T(wa, wb). Следовательно, количество шагов T может сильно различаться между соседними парами чисел, такими как (a, b) и (a, b+1), так как данная величина зависит от НОД.
Рекурсивный характер алгоритма Евклида даёт следующее уравнение T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1, где T(x, 0) = 0 по предположению.[17]
Рекурсивный характер алгоритма Евклида даёт следующее уравнение T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1, где T(x, 0) = 0 по предположению.[17]
Слайд 4НАИХУДШИЙ СЛУЧАЙ
Если для алгоритма Евклида требуются N шагов для пары натуральных чисел
НАИХУДШИЙ СЛУЧАЙ
Если для алгоритма Евклида требуются N шагов для пары натуральных чисел

a > b > 0, наименьшие значения a и b, для которых это выполняется — числа Фибоначчи FN+2 и FN+1 соответственно.[27] Тогда, если алгоритм Евклида требует N шагов для пары чисел (a,b), где a > b, выполняются следующие неравенства a ≥ FN+2 и b ≥ FN+1. Доказать это можно по математической индукции. Если N = 1, тогда a делится на b без остатка. Наименьшие натуральные числа, для которых это верно, равны b = 1 и a = 2, соответственно F2 и F3. Предположим теперь, что результат выполняется для всех значений N до M − 1. Первый шаг алгоритма Евклида с M шагами a = q0b + r0, и алгоритм Евклида для пары чисел (b,r0), где b > r0, требует M − 1 шагов. По предположению индукции имеем b ≥ FM+1 и r0 ≥ FM. Следовательно, a = q0b + r0 ≥ b + r0 ≥ FM+1 + FM = FM+2, что является искомым неравенством. Это доказательство, опубликованное Габриэлем Ламе в 1844 году, представляет собой начало теории сложности вычислений,[28] а также первое практическое применение чисел Фибоначчи.[27]
Слайд 5ТЕОРЕМА ЛАМЕ
Число делений с остатком в процессе применения алгоритма Евклида не превосходит
ТЕОРЕМА ЛАМЕ
Число делений с остатком в процессе применения алгоритма Евклида не превосходит

упятеренного количества цифр меньшего числа {\displaystyle b}b, записанного в десятичной системе.[29]
Слайд 6СРЕДНЕЕ
Существуют различные способы вычисления среднего количества шагов алгоритма. Первый способ вычисления —
СРЕДНЕЕ
Существуют различные способы вычисления среднего количества шагов алгоритма. Первый способ вычисления —

среднее время T(a), необходимое для вычисления НОД заданного числа a и меньшего натурального числа b, выбранного с равной вероятностью из целых чисел от 0 до a − 1.[17]
{\displaystyle T(a)={\frac {1}{a}}\sum _{0\leq bОднако, поскольку T(a, b) сильно колеблется в зависимости от НОД двух чисел, усреднённая функция T(a) также является «шумной».[30] Для того, чтобы уменьшить этот шум, второе среднее τ(a) берётся по всем взаимно простым числам с a.
{\displaystyle \tau (a)={\frac {1}{\varphi (a)}}\sum _{\begin{smallmatrix}0\leq bгде φ(a) функция Эйлера. Это среднее плавно растёт с ростом a.[31]
{\displaystyle \tau (a)={\frac {12}{\pi ^{2}}}\ln 2\ln a+C+O(a^{-1/6-\varepsilon })}{\displaystyle \tau (a)={\frac {12}{\pi ^{2}}}\ln 2\ln a+C+O(a^{-1/6-\varepsilon })}
Константа (константа Портера[32]) в этой формуле {\displaystyle C\approx 1.467}{\displaystyle C\approx 1.467}, а ε является бесконечно малым.
Третье среднее значение Y(n) определяется как среднее число шагов, требуемых, когда a и b выбираются случайным образом (с равномерным распределением) от 1 до n.
{\displaystyle Y(n)={\frac {1}{n^{2}}}\sum _{a=1}^{n}\sum _{b=1}^{n}T(a,b)={\frac {1}{n}}\sum _{a=1}^{n}T(a).}{\displaystyle Y(n)={\frac {1}{n^{2}}}\sum _{a=1}^{n}\sum _{b=1}^{n}T(a,b)={\frac {1}{n}}\sum _{a=1}^{n}T(a).}
{\displaystyle T(a)={\frac {1}{a}}\sum _{0\leq b
{\displaystyle \tau (a)={\frac {1}{\varphi (a)}}\sum _{\begin{smallmatrix}0\leq b
{\displaystyle \tau (a)={\frac {12}{\pi ^{2}}}\ln 2\ln a+C+O(a^{-1/6-\varepsilon })}{\displaystyle \tau (a)={\frac {12}{\pi ^{2}}}\ln 2\ln a+C+O(a^{-1/6-\varepsilon })}
Константа (константа Портера[32]) в этой формуле {\displaystyle C\approx 1.467}{\displaystyle C\approx 1.467}, а ε является бесконечно малым.
Третье среднее значение Y(n) определяется как среднее число шагов, требуемых, когда a и b выбираются случайным образом (с равномерным распределением) от 1 до n.
{\displaystyle Y(n)={\frac {1}{n^{2}}}\sum _{a=1}^{n}\sum _{b=1}^{n}T(a,b)={\frac {1}{n}}\sum _{a=1}^{n}T(a).}{\displaystyle Y(n)={\frac {1}{n^{2}}}\sum _{a=1}^{n}\sum _{b=1}^{n}T(a,b)={\frac {1}{n}}\sum _{a=1}^{n}T(a).}
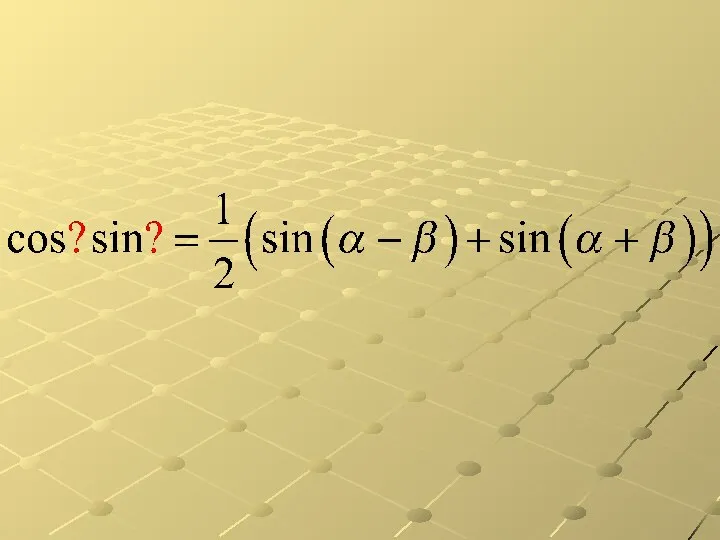 Тригонометрические формулы. Диктант
Тригонометрические формулы. Диктант Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Чертежи и развертки простых геометрических тел
Чертежи и развертки простых геометрических тел Презентация на тему Луч и угол (7 класс)
Презентация на тему Луч и угол (7 класс)  Графики степенных функций
Графики степенных функций Коварные диаграммы
Коварные диаграммы Площадь треугольника
Площадь треугольника Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Понятие о проценте
Понятие о проценте Задачи на проценты
Задачи на проценты Многоугольники в нашей жизни
Многоугольники в нашей жизни Последовательность трехзначных чисел
Последовательность трехзначных чисел Равнобедренный треугольник
Равнобедренный треугольник Симметрия вокруг нас
Симметрия вокруг нас Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Создание геометрических тел
Создание геометрических тел Построение сечений тетраэдра
Построение сечений тетраэдра Код Церетели
Код Церетели Презентация на тему Действия с натуральными числами
Презентация на тему Действия с натуральными числами  Сравнение чисел
Сравнение чисел Числовой коэффициент
Числовой коэффициент Тренажер Вычисление производных
Тренажер Вычисление производных Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Какие бывают графы
Какие бывают графы Комбинаторные задачи
Комбинаторные задачи Деление дробей. 6 класс
Деление дробей. 6 класс