Слайд 2Определение
Многогранник, у которого одна грань, (называемая основанием), - многоугольник, а другие грани

- треугольники с общей вершиной, называется пирамидой.
Слайд 3вершина
высота
Боковые грани
основание
апофема
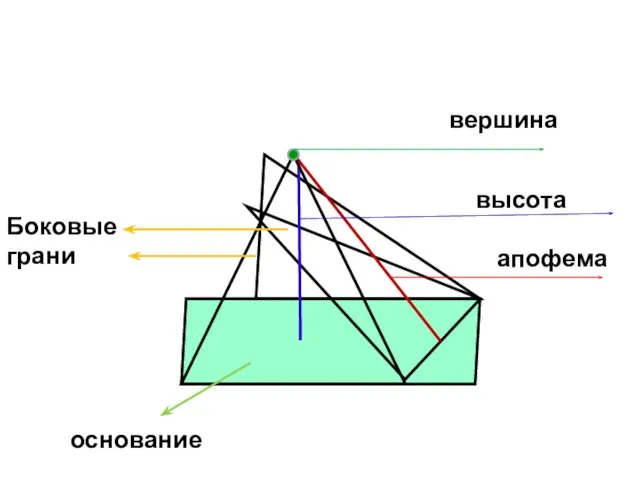
Слайд 4Общая вершина боковых граней называется вершиной пирамиды.
Грани, отличные от основания, называются

боковыми.
Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание.
Длина этого перпендикуляра обозначается буквой H.
Слайд 5Пирамида называется правильной,
если ее основание – правильный
многоугольник, а высота проходит через
центр основания.

Сечение пирамиды плоскостью,
проходящей через вершину и диагональ
основания, называется диагональным
сечением.
Обозначая пирамиду, сначала называют ее вершину, а затем - вершины основания.
Апофемой боковой грани правильной пирамиды называется высота этой грани, проведённая из вершины пирамиды.
Слайд 6где A - апофема боковой грани,
P - периметр основания
Для правильной пирамиды

справедлива формула
Слайд 7Определение
Часть пирамиды, лежащая между основанием и параллельным основанию сечением, называется усеченной пирамидой.

Слайд 8Боковые грани усеченной
пирамиды - трапеции
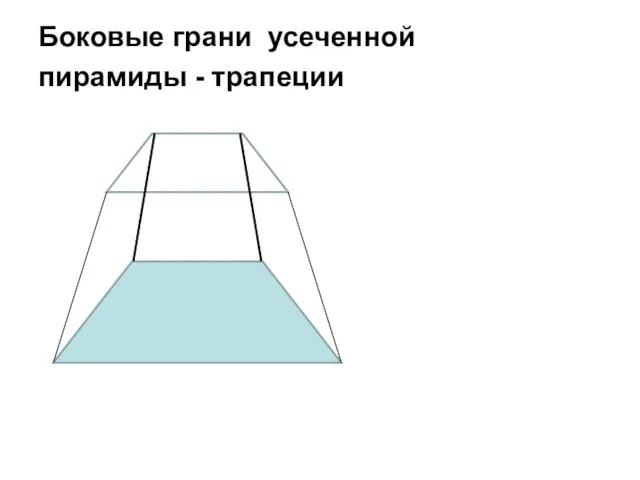
Слайд 9Основания усеченной пирамиды - подобные многоугольники. Если полная пирамида правильная, то и

соответствующая усеченная пирамида - правильная.
Высота усеченной пирамиды - это общий
перпендикуляр к плоскостям ее оснований
(или его длина).
Апофемой правильной усеченной пирамиды
называется часть апофемы полной
пирамиды, ограниченная плоскостями
оснований усеченной пирамиды, т.е. отрезок,
соединяющий середины параллельных
сторон боковой грани.








 Задача на процкеты
Задача на процкеты Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Построение сечений
Построение сечений Функции и графики
Функции и графики Степенные функции
Степенные функции Моделирование на графах
Моделирование на графах Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед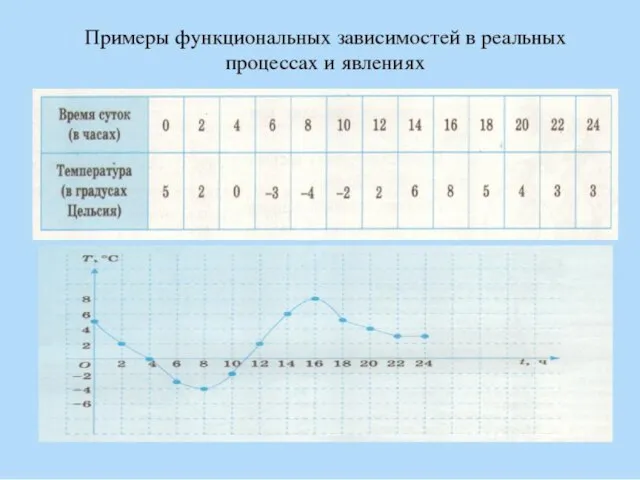 График функции. Примеры
График функции. Примеры В мире рациональных уравнений
В мире рациональных уравнений Возникновение слова “процент”. Древний Рим
Возникновение слова “процент”. Древний Рим Аксиомы планиметрии (часть 2)
Аксиомы планиметрии (часть 2) Квадратные корни
Квадратные корни Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики Делители и кратные
Делители и кратные Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Решение логических задач
Решение логических задач Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Признаки параллельности двух прямых
Признаки параллельности двух прямых Золотое сечение (продолжение)
Золотое сечение (продолжение) Сфера и шар. Уравнение сферы
Сфера и шар. Уравнение сферы Математика на кухне
Математика на кухне Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Усовершенствование навыков действий с рациональными числами
Усовершенствование навыков действий с рациональными числами Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Исследование функции
Исследование функции Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения