Слайд 2Упорядоченные множества
Наиболее простым упорядоченным множеством является двухэлементное множество, которое называют двойкой или

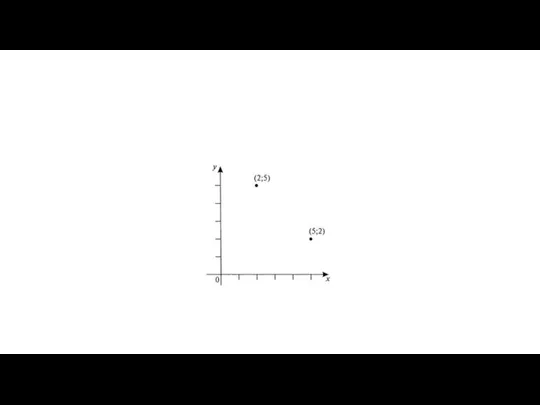
упорядоченной парой. Элементы упорядоченного множества обычно заключают в круглые или угловые скобки. Например, (2;5) или < 2;5 >.
Определение: Если (a, b) — упорядоченная пара, то элемент a называют первым элементом или первой компонентой этой пары, а элемент b — вторым элементом или второй компонентой этой же пары.
Каждое упорядоченное множество можно определить с помощью неупорядоченных множеств. Например, двойку определяют так:
(a,b)={{a},{a,b}}
Слайд 4Тройку определяют через двойку:
Аналогично, n-ку определяют через двойку:
Введенное понятие упорядоченного

множества позволяет определить новую операцию на множествах.
Прямым (декартовым) произведением
Слайд 5Прямое произведение множеств

Слайд 6Имеется графическая интерпретация прямого произведения множеств. Пусть множество
есть интервал значений переменной

x и
есть интервал значений у. Ясно, что множества А и В имеют бесконечное число элементов. Тогда прямое (декартово) произведение множеств А и В есть множество точек прямоугольника:
Слайд 7Декартово произведение множеств

Слайд 9Бинарные отношения
Бинарное отношение — это отношение между двумя объектами.
Бинарное отношение можно определить

как совокупность упорядоченных пар, указывающих объекты, находящиеся в данном отношении.
Если два элемента a и b находятся в данном отношении R, то (a,b)∈R, или aRb.
Всякое бинарное отношение R можно рассматривать как подмножество прямого произведения некоторых множеств А и В:
Слайд 10Левой областью бинарного отношения R называют множество всех первых компонент упорядоченных пар,

составляющих данное отношение, то есть
Правой областью бинарного отношения R называют множество всех вторых компонент упорядоченных пар, составляющих данное отношение, то есть
Слайд 13Способы задания бинарных отношений
1. Бинарное отношение R можно задать перечислением всех упорядоченных

пар, находящихся в отношении R.
2. Можно задать формулой.
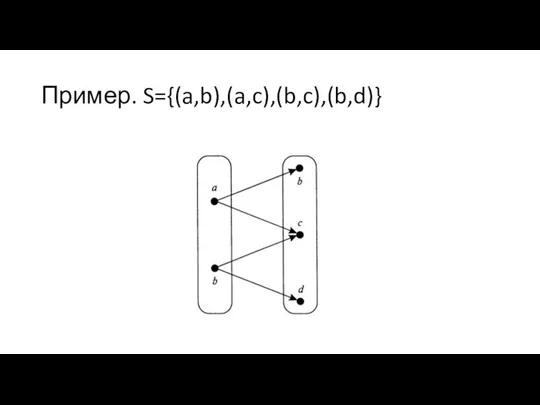
3. Графическое задание бинарного отношения предполагает графическое представление элементов левой и правой областей отношения в виде точек в этих областях, соединенных дугами.
Слайд 14Пример. S={(a,b),(a,c),(b,c),(b,d)}
Слайд 154. Бинарное отношение R может быть задано в табличной форме.

Слайд 165. Бинарное отношение можно задать матрицей ||aij||, в которой строки и столбцы

соответствуют полю отношения. В этой матрице i-я строка соотносится с некоторым элементом левой области отношения, j-й столбец — с некоторым элементом правой области отношения. Тогда aij = 1, если соответствующие элементы находятся в данном отношении, и aij = 0 в противном случае.
Слайд 17Операции над бинарными отношениями
Так как всякое бинарное отношение — это множество упорядоченных

пар, то над бинарными отношениями можно выполнять все теоретико-множественные операции: объединение, пересечение, разность, дополнение.
Слайд 20Свойства бинарных отношений.
Отношение эквивалентности

Слайд 23Бинарное отношение R называют антисимметричным, если из aRb и bRa следует, что

а = b.
Бинарное отношение R называют транзитивным, если из aRb и bRc следует, что aRc.
Примерами транзитивных отношений являются отношение равенства (=), отношение подобия ( ~ ), отношения порядка (<), (<), (>), (>), (с), отношение параллельности (||).
В противном случае отношение R называют нетранзитивным.
Бинарное отношение называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Примеры отношения эквивалентности: отношение равенства (=),
отношение параллельности (||).
Слайд 26Отношение порядка
Бинарное отношение R называют отношением порядка, если оно антисимметрично и

транзитивно. Если к тому же это отношение антирефлексивно, то такое отношение называется отношением строгого порядка. В противном случае мы имеем отношение нестрогого порядка.






















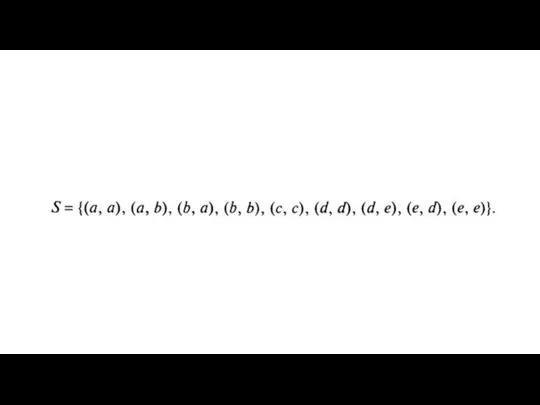

 Логарифмы и их свойства
Логарифмы и их свойства Показатели вариации
Показатели вариации Аналитическое (письменное) счисление координат
Аналитическое (письменное) счисление координат Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Математика в пределах десяти
Математика в пределах десяти ОГЭ 20-21. Задачи
ОГЭ 20-21. Задачи Решение задач. Штрих Шеффера
Решение задач. Штрих Шеффера Тригонометрические уравнения. Частные случаи
Тригонометрические уравнения. Частные случаи Построение сечений многогранников
Построение сечений многогранников Расстояния в пространстве
Расстояния в пространстве Задания по математике (5 класс, часть 3)
Задания по математике (5 класс, часть 3) Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Дифференциальное исчисление элементарной и сложной функции функции
Дифференциальное исчисление элементарной и сложной функции функции Комплексные числа и квадратные уравнения
Комплексные числа и квадратные уравнения Решение тригонометрических уравнений
Решение тригонометрических уравнений Сравнение дробей
Сравнение дробей Все способы решения тригонометрических уравнений
Все способы решения тригонометрических уравнений Числовые промежутки. Пересечение и объединение промежутков
Числовые промежутки. Пересечение и объединение промежутков Тела вращения. Математический диктант
Тела вращения. Математический диктант Основные способы преобразования графиков
Основные способы преобразования графиков Применение свойств арифметических действий сложения и вычитания для рационализации вычисления
Применение свойств арифметических действий сложения и вычитания для рационализации вычисления Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции
Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания
РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания Решение задач на нахождение значений двух величин по сумме и разности
Решение задач на нахождение значений двух величин по сумме и разности Решение задач по теме: Параллелограммы вокруг нас (2)
Решение задач по теме: Параллелограммы вокруг нас (2) Сечения параллелепипеда
Сечения параллелепипеда Конкретный смысл действия деления
Конкретный смысл действия деления Презентация на тему Векторы в пространстве Геометрия
Презентация на тему Векторы в пространстве Геометрия