Содержание
- 2. Производная Производная функции это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента. Приращением
- 3. Вычисление производных
- 5. Правило дифференцирования (нахождение производной)
- 7. Физический смысл производной
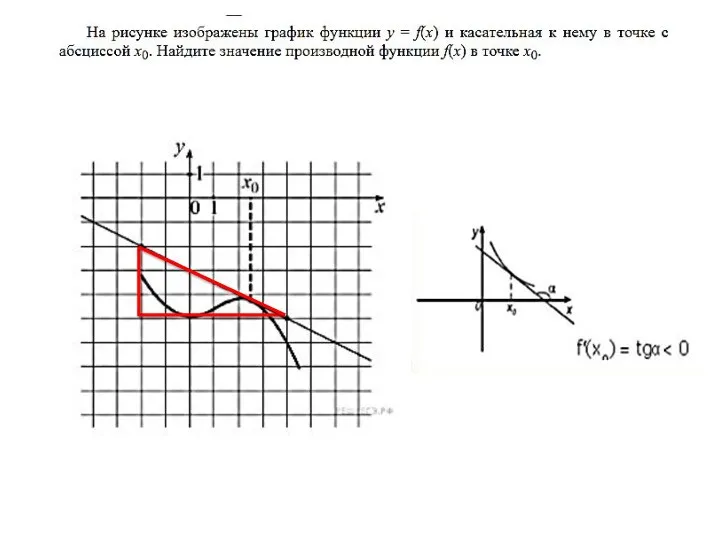
- 8. Примеры заданий
- 9. 20 59 8
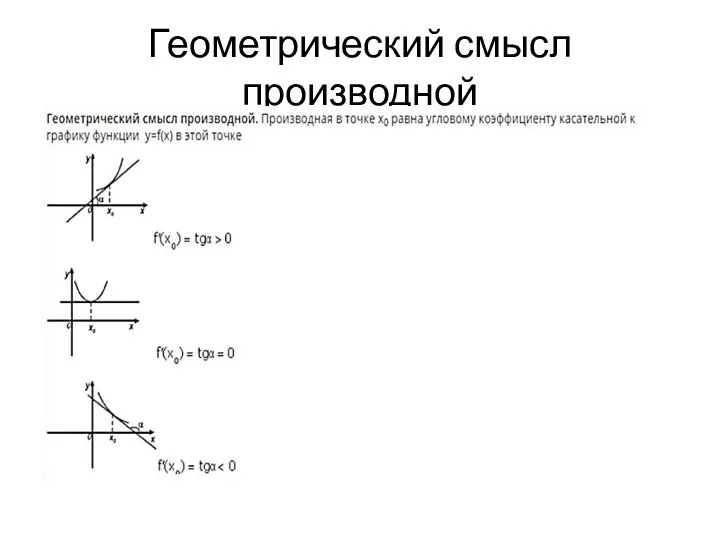
- 10. Геометрический смысл производной
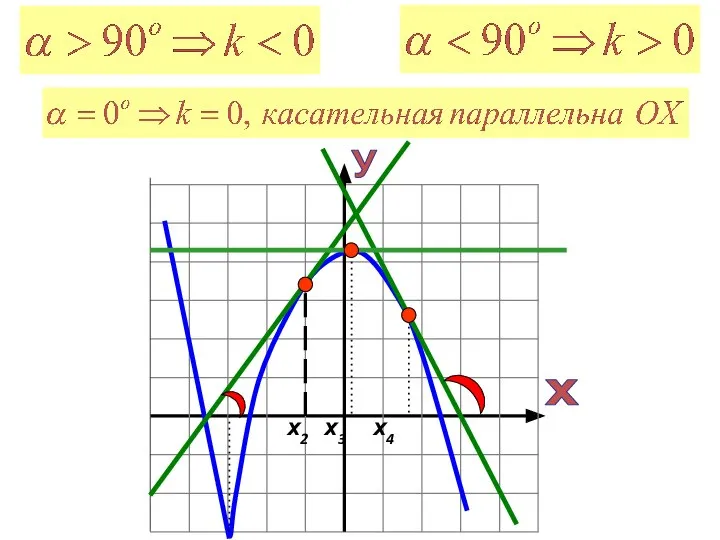
- 12. Уравнение касательной
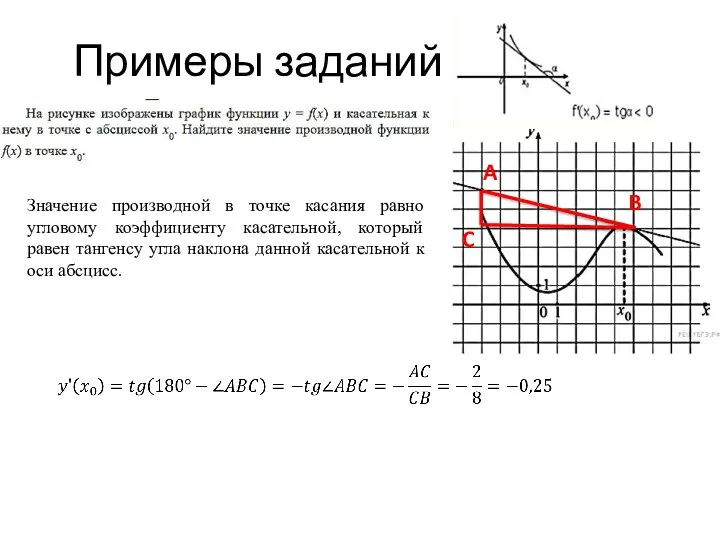
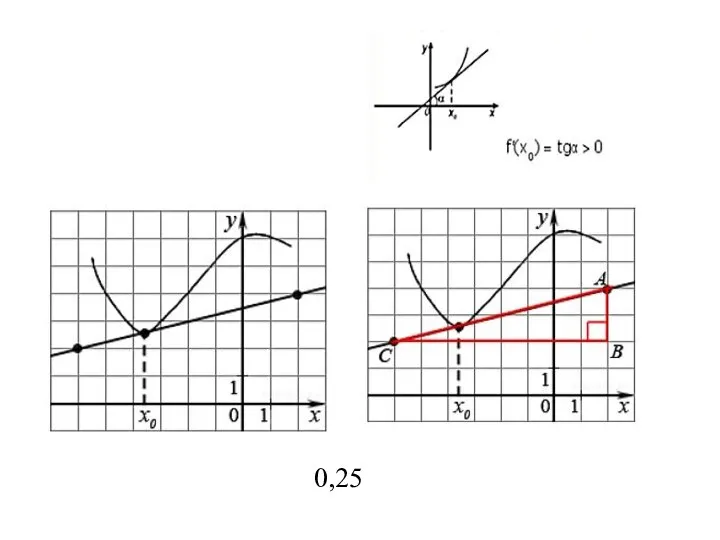
- 13. Примеры заданий Значение производной в точке касания равно угловому коэффициенту касательной, который равен тангенсу угла наклона
- 15. 0,25
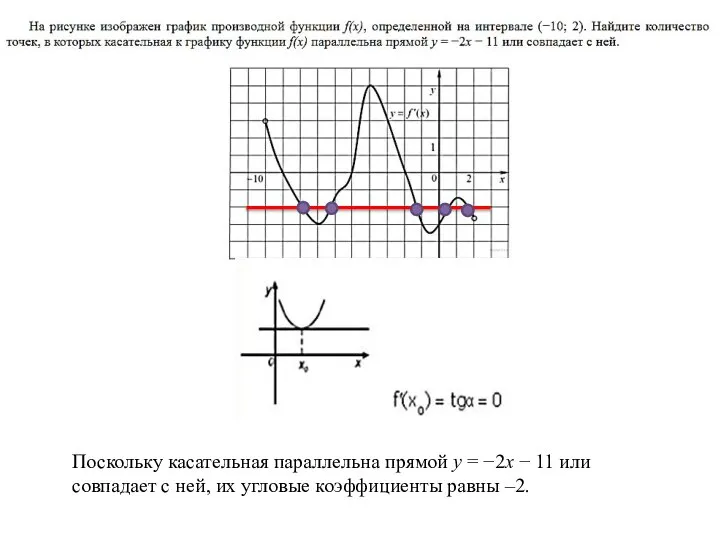
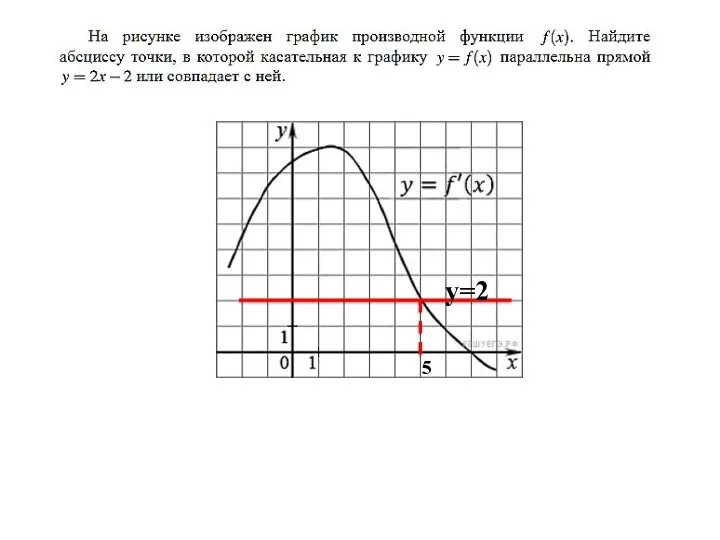
- 16. Примеры заданий Поскольку касательная параллельна прямой y = −2x − 11 или совпадает с ней, их
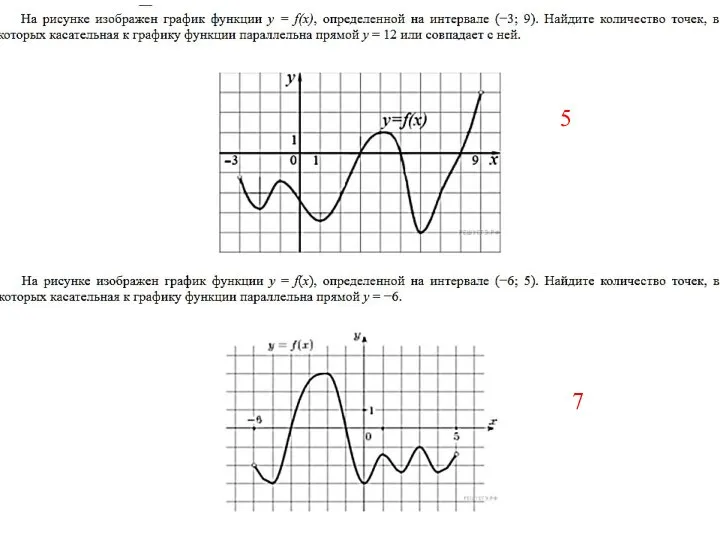
- 18. 5 7
- 19. 5
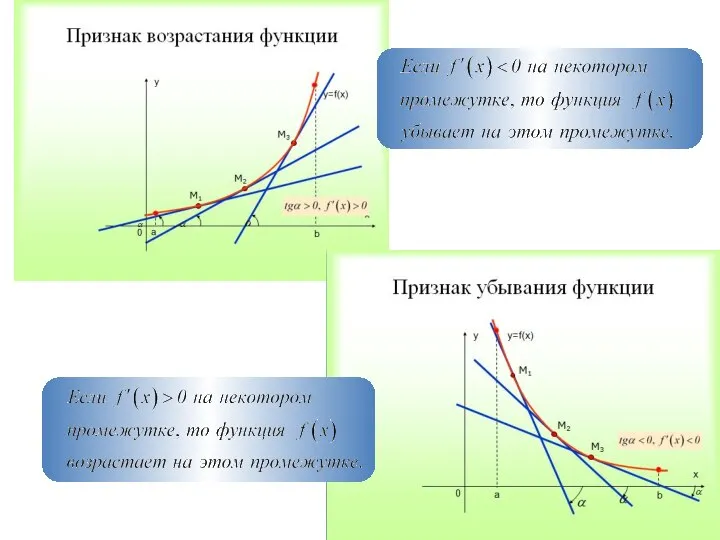
- 21. Применение производной к исследованию функции
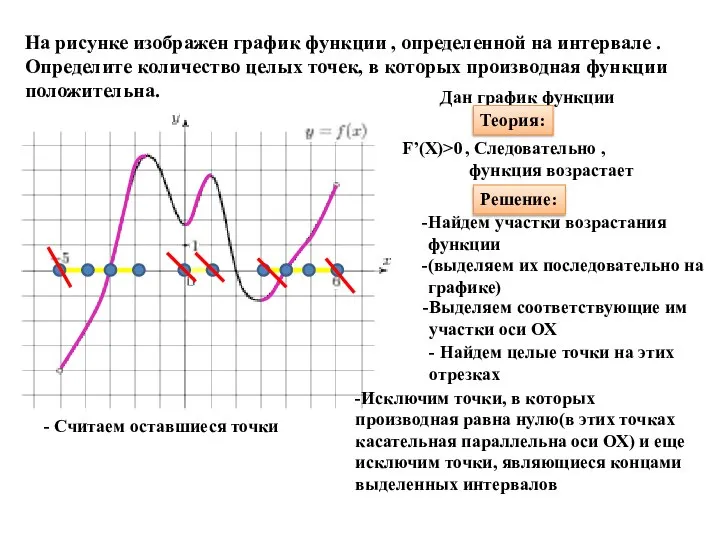
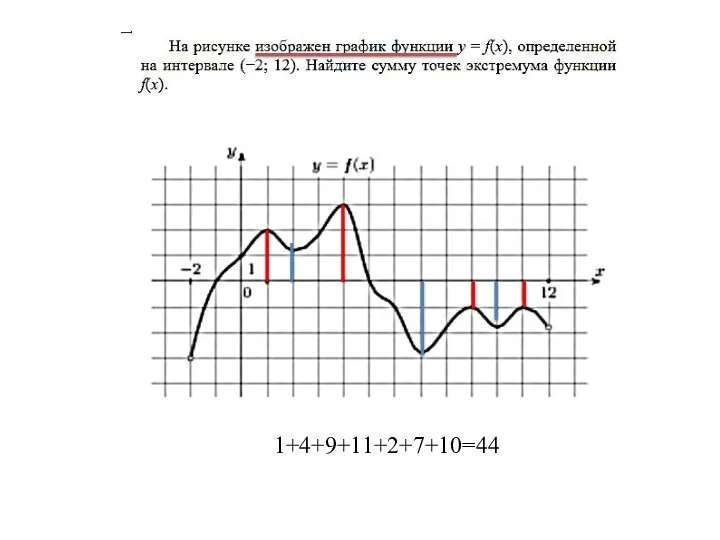
- 23. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых
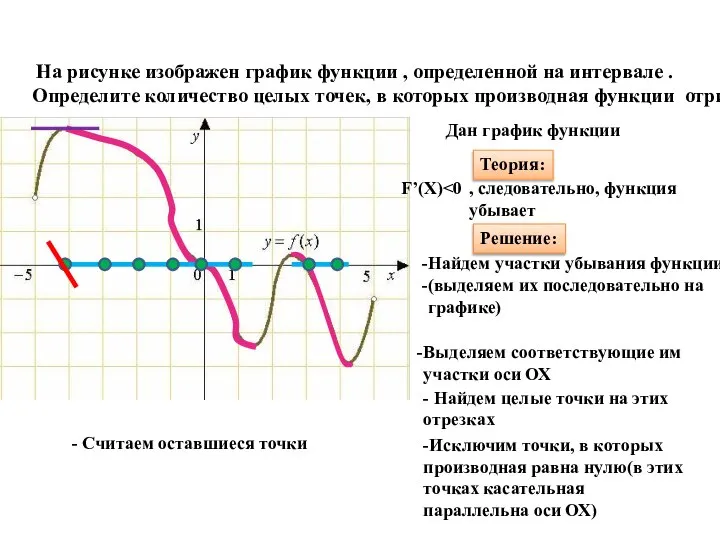
- 24. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых
- 25. 1+4+9+11+2+7+10=44
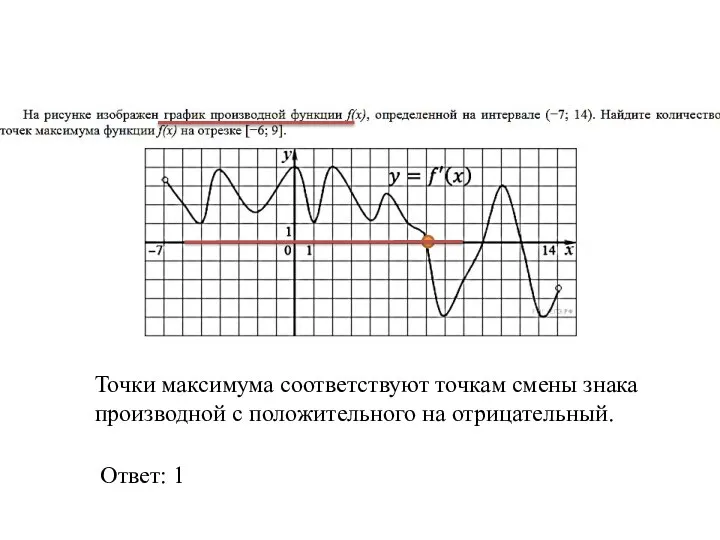
- 26. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Ответ: 1
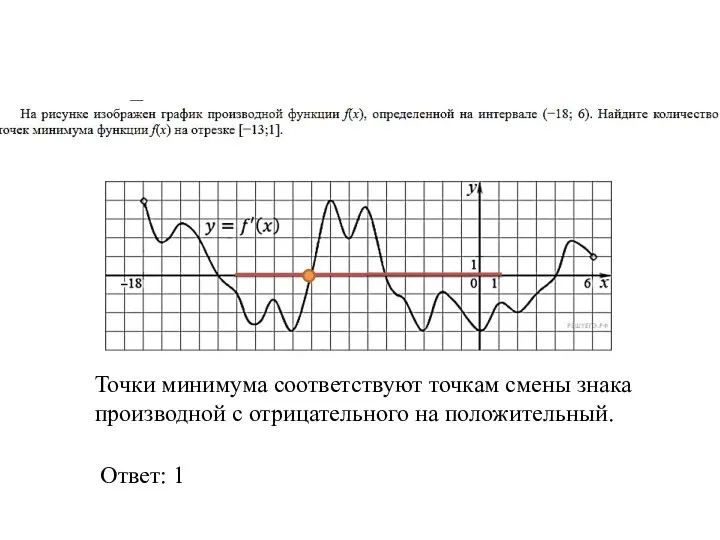
- 27. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. Ответ: 1
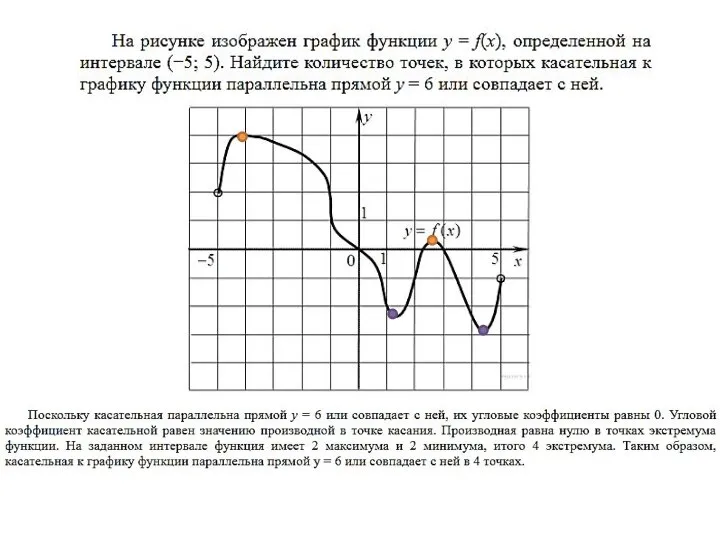
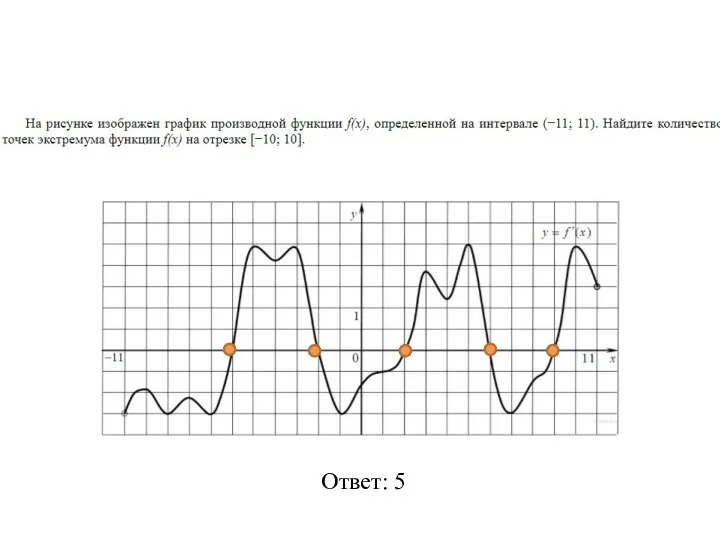
- 28. Ответ: 5
- 30. Скачать презентацию











 Сокращение дробей. Тождество
Сокращение дробей. Тождество Куб. Прямоугольный параллелепипед
Куб. Прямоугольный параллелепипед Умножение. Законы умножения
Умножение. Законы умножения Решение систем уравнений
Решение систем уравнений Презентация на тему Теорема косинусов
Презентация на тему Теорема косинусов  Иллюзии и математические парадоксы
Иллюзии и математические парадоксы Сложение и вычитание векторов. Демонстрационный материал. 9 класс
Сложение и вычитание векторов. Демонстрационный материал. 9 класс Урок цифры в Республике Татарстан
Урок цифры в Республике Татарстан Помоги ёжику. Интерактивный тренажёр по математике, 1 класс
Помоги ёжику. Интерактивный тренажёр по математике, 1 класс Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной Построение графика функции
Построение графика функции Показательная функция и ее применение
Показательная функция и ее применение Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Виды чисел
Виды чисел Расчёт частотных и импульсных характеристик БИХ-цепей 1-го порядка
Расчёт частотных и импульсных характеристик БИХ-цепей 1-го порядка Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Задание 2 по математике
Задание 2 по математике Сложение вида +7
Сложение вида +7 Сравнение выражений
Сравнение выражений Деление
Деление Решение примеров
Решение примеров Цена, количество, стоимость
Цена, количество, стоимость Арифметическая прогрессия
Арифметическая прогрессия Числовые промежутки
Числовые промежутки Аксиомы
Аксиомы Тангенс суммы и разности аргументов
Тангенс суммы и разности аргументов Адмирал Морского Флота Федор Федорович Ушаков
Адмирал Морского Флота Федор Федорович Ушаков Особенности набора математических формул в Microsoft
Особенности набора математических формул в Microsoft