Содержание
- 2. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА План 1. Різні рівняння площини 2. Кут між двома площинами 3. Відстань
- 3. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Загальне рівняння площини Нехай площина проходить через точку
- 4. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Загальне рівняння площини Одержане рівняння запишемо в координатній
- 5. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Частинні випадки загального рівняння площини .
- 6. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Частинні випадки загального рівняння площини 3. Якщо дорівнюють
- 7. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Рівняння площини, яка проходить через три задані точки
- 8. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Рівняння площини, яка проходить через три задані точки
- 9. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Рівняння площини у відрізках на осях Нехай площина
- 10. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини Рівняння площини у відрізках на осях Розкривши визначник,
- 11. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 2. Кут між двома площинами Нехай Косинус кута між цими векторами, а
- 12. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 2. Кут між двома площинами
- 13. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 3. Відстань від точки до площини до площини Вона має вигляд:
- 14. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Канонічне рівняння прямої в просторі
- 15. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Канонічне рівняння прямої в просторі
- 16. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Рівняння прямої, яка проходить через
- 17. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Рівняння прямої, яка проходить через
- 18. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Параметричне рівняння прямої Позначимо значення
- 19. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Рівняння прямої, як лінія перетину
- 20. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Рівняння прямої, як лінія перетину
- 21. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі Рівняння прямої, як лінія перетину
- 22. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 5. Кут між двома прямими в просторі
- 23. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 5. Кут між двома прямими в просторі
- 24. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 6. Кут між прямою і площиною Нехай пряму задано канонічним рівнянням площину
- 25. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань Приклад. Знайти рівняння площини, яка проходить через
- 26. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань Розв’язання. По формулі якщо врахувати, що одержимо:
- 27. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань Розв’язання. Відстань від точки до площини обчислюємо
- 28. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань Розв’язання. Направляючий вектор цієї прямої обчислимо за
- 29. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань Покладемо z=0 і знайдемо розв’язок системи Розв’язавши
- 30. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 8. Запитання для самоконтролю 1.Записати загальне рівняння площини і дати геометричне пояснення
- 31. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 8. Запитання для самоконтролю 6. Записати формулу косинуса кута між двома площинами.
- 33. Скачать презентацию






























 Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Практикум. Демографические задачи
Практикум. Демографические задачи Тренажёры ЕГЭ
Тренажёры ЕГЭ Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10
Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10 Что такое медиана?
Что такое медиана? Закрепление таблицы умножения и деления
Закрепление таблицы умножения и деления Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Симметрия вокруг нас
Симметрия вокруг нас Средняя линия треугольника
Средняя линия треугольника Способы задания зависимостей между величинами: аналитический, табличный, графический
Способы задания зависимостей между величинами: аналитический, табличный, графический Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Понятие цилиндра
Понятие цилиндра Интерактивная игра Состав числа в пределах первого десятка
Интерактивная игра Состав числа в пределах первого десятка Возмущения линейных систем и проматрицы
Возмущения линейных систем и проматрицы Инженерно-вычислительные технологии
Инженерно-вычислительные технологии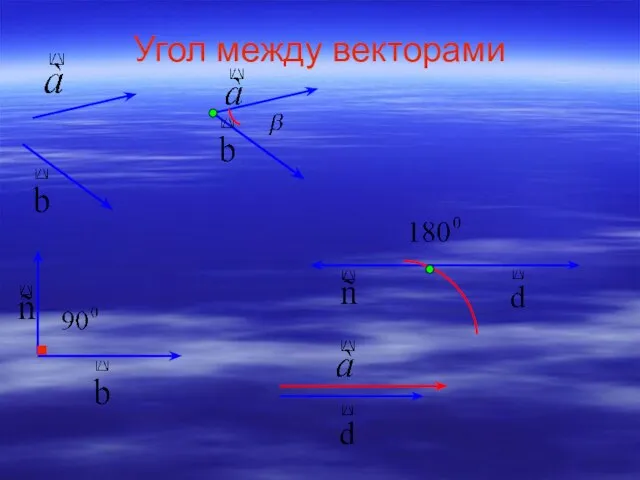 Презентация на тему Угол между векторами и скалярное произведение векторов
Презентация на тему Угол между векторами и скалярное произведение векторов  Построение симметричных фигур
Построение симметричных фигур Объемы тел вращения
Объемы тел вращения Методы решения тригонометрических уравнений. 10 класс
Методы решения тригонометрических уравнений. 10 класс Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Графический метод решения уравнений с параметром
Графический метод решения уравнений с параметром Развертка сферы
Развертка сферы Математический диктант. Классная работа
Математический диктант. Классная работа Презентация на тему Начертательная геометрия
Презентация на тему Начертательная геометрия  Презентация на тему Итоговое повторение курса алгебры за 8 класс
Презентация на тему Итоговое повторение курса алгебры за 8 класс  тригонометрия 1 урок
тригонометрия 1 урок Принятие решений о прикреплении оптовых потребителей к поставщикам
Принятие решений о прикреплении оптовых потребителей к поставщикам К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна»
К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна»