- Главная
- Математика
- Представление чисел с плавающей запятой

Содержание
- 2. Вещественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере в формате с плавающей
- 3. Определение максимального числа обычной точности Число обычной точности занимает в памяти компьютера 4 байта. Для хранения
- 4. Максимальное значение мантиссы Точность вычислений определяется количеством разрядов, отведённых для хранения мантиссы чисел. 223 - 1≈
- 5. Сложение и вычитание чисел в формате с плавающей запятой. Сначала проводится подготовительная операция выравнивание порядков. Меньший
- 6. Умножение и деление чисел с плавающей запятой При умножении чисел в формате с плавающей запятой порядки
- 8. Скачать презентацию
Слайд 2Вещественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере
Вещественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере

Формат чисел с плавающей запятой базируется на экспоненциальной форме записи в которой может быть представлено любое число.
A=m×qn
где m – мантисса числа, 1/n ≤|m|< 1
q - основание системы счисления,
n - порядок числа.
Мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.
Приведение числа с плавающей запятой к нормализованной форме
888,888 = 0,888888 × 10 3
Нормализованная мантисса m=0,8888888, порядок n=3.
Слайд 3Определение максимального числа
обычной точности
Число обычной точности занимает в памяти компьютера 4 байта.
Для
Определение максимального числа
обычной точности
Число обычной точности занимает в памяти компьютера 4 байта.
Для

Максимальное значение порядка числа составит
11111112 =12710
Максимальное число
2127 = 1,7014118346046923173168730371588 × 1038
Число двойной точности занимает в памяти компьютера 8 байтов.
Слайд 4Максимальное значение мантиссы
Точность вычислений определяется количеством разрядов, отведённых для хранения мантиссы чисел.
223
Максимальное значение мантиссы
Точность вычислений определяется количеством разрядов, отведённых для хранения мантиссы чисел.
223

Таким образом, максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 × 1038
(количество значащих цифр десятичного числа в данном случае ограниченно
7 разрядами)
Слайд 5 Сложение и вычитание чисел
в формате с плавающей запятой.
Сначала проводится подготовительная
Сложение и вычитание чисел
в формате с плавающей запятой.
Сначала проводится подготовительная

Меньший по модулю порядок увеличивается до величины большего по модулю порядка числа. Для того чтобы величина числа не изменилась, мантисса уменьшается в такое же количество раз (сдвигается в ячейке памяти вправо на количество разрядов, равное разрядности порядков чисел).
После выполнения операции выравнивания одинаковые разряды чисел оказываются расположенными в одних и тех же разрядах ячеек памяти. Теперь операции сложения и вычитания чисел сводятся к сложению или вычитанию мантисс.
0,1 × 25 + 0,1 × 23 = ? 0,1 × 25 - 0,1 × 23 = ?
0,100 × 25 0,100 × 25
+ -
0,001 × 25 0,001 × 25
______________ _________________
0,101 × 25 0,010 × 25 = 0,10 × 24
Слайд 6
Умножение и деление чисел с плавающей запятой
При умножении чисел в формате с
Умножение и деление чисел с плавающей запятой
При умножении чисел в формате с

При делении из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя.
Затем число обязательно нормализуется, т. е. после запятой должна стоять цифра, отличная от нуля.
Умножение
0,1 × 25
× 0,1 × 23
______________
0,01 × 28 = 0,1 × 27
Деление
0,1 × 25
: 0,1 × 23
______________
1 × 22 = 0,1 × 23
 Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи
Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века
Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века Иррациональные уравнения
Иррациональные уравнения Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Решение задач на одновременное встречное движение
Решение задач на одновременное встречное движение Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Вычисление дробей
Вычисление дробей ЕГЭ по математике. Экономические задачи VII
ЕГЭ по математике. Экономические задачи VII Презентация на тему Смешанные числа (5 класс)
Презентация на тему Смешанные числа (5 класс)  Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Знакомство с цифрой 5
Знакомство с цифрой 5 Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Пирамида. Развёртка пирамиды
Пирамида. Развёртка пирамиды Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Учимся писать цифры
Учимся писать цифры Презентация по математике "Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей" -
Презентация по математике "Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей" -  Проценты. Часть 2
Проценты. Часть 2 Производная сложной функции
Производная сложной функции Приближенные формулы Лапласа и Пуассона
Приближенные формулы Лапласа и Пуассона Девиз урока: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и
Девиз урока: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и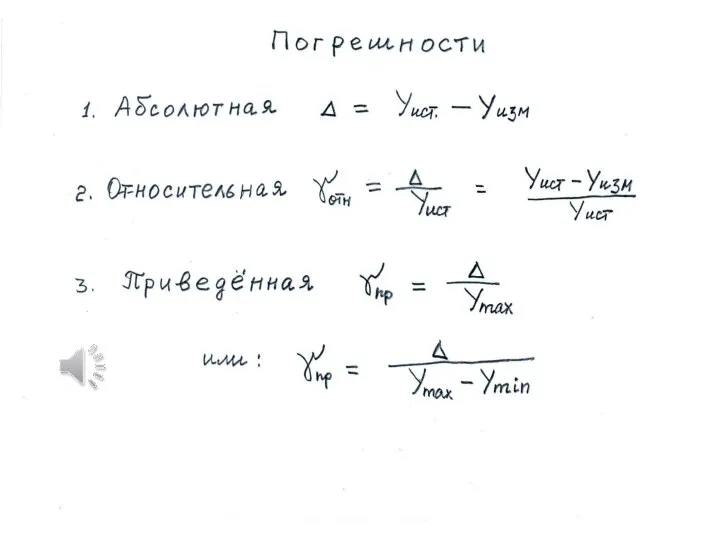 Погрешности. Погрешности измерений
Погрешности. Погрешности измерений Десятичные дроби. Уравнения
Десятичные дроби. Уравнения Формирование элементарных математических представлений
Формирование элементарных математических представлений Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Основы теории измерений
Основы теории измерений розвязування трикутників
розвязування трикутників Расчет количества половой краски
Расчет количества половой краски