Содержание
- 2. Лекция 2. Ортогональные проекции прямой линии Способы задания прямой линии Прямые общего положения Прямые частного положения
- 3. Прямая линия – кратчайшее расстояние между двумя точками Задание прямой линии: Аналитическим способом Графическими способами
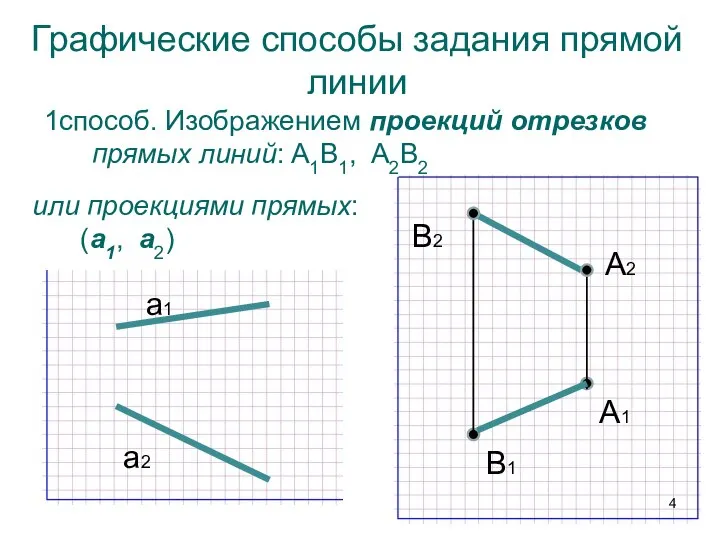
- 4. Графические способы задания прямой линии B2 B1 А2 А1 1способ. Изображением проекций отрезков прямых линий: A1B1,
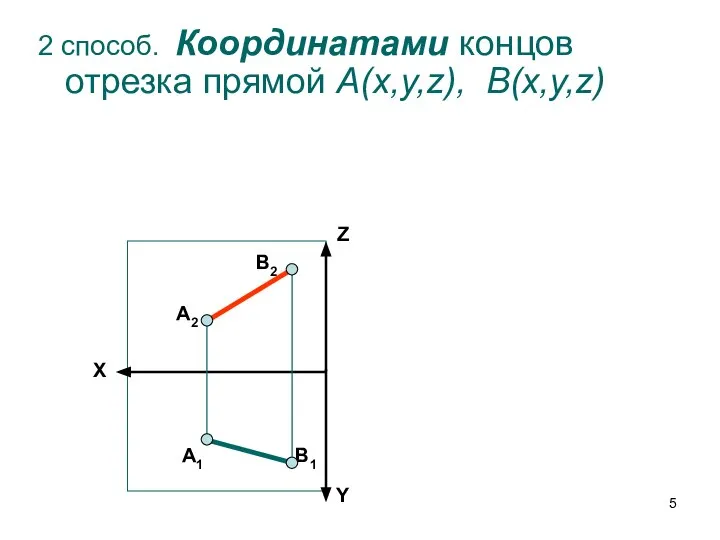
- 5. X Z Y А2 А1 В2 В1 2 способ. Координатами концов отрезка прямой А(x,y,z), В(x,y,z)
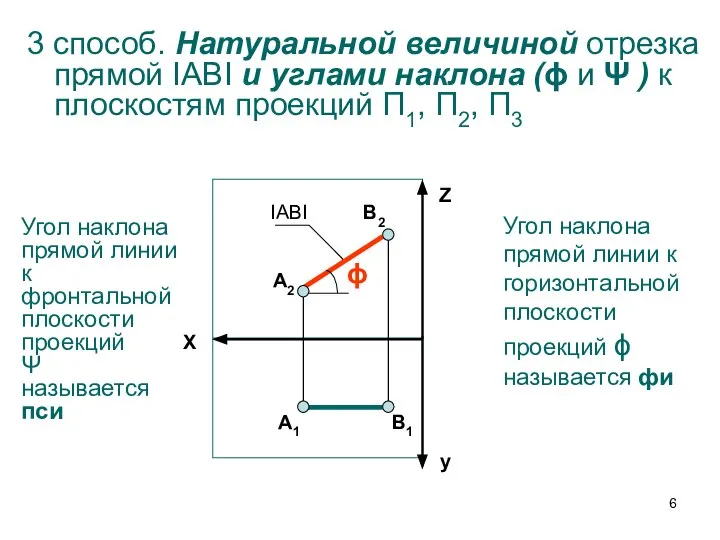
- 6. 3 способ. Натуральной величиной отрезка прямой IABI и углами наклона (ϕ и Ψ ) к плоскостям
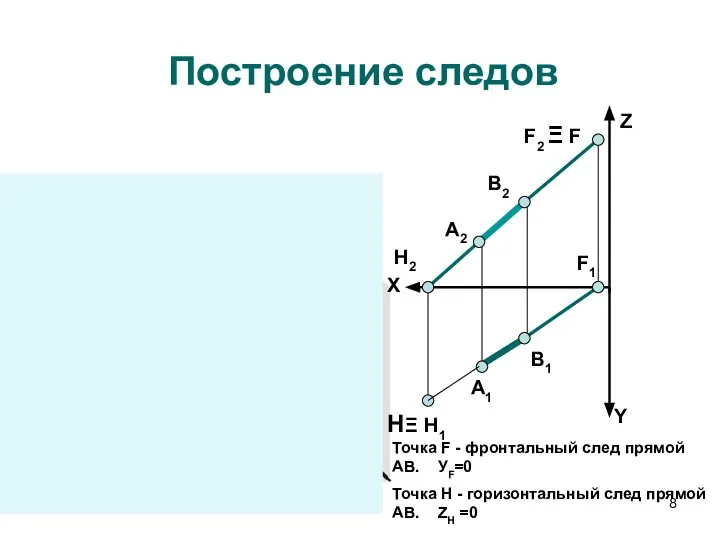
- 7. 4 способ. Задание прямой ее следами Следом прямой линии называется точка пересечения прямой с плоскостью проекций
- 8. А1 А2 Z Y X П1 П3 П2 В1 В2 Z Y В1 А2 В2 Построение
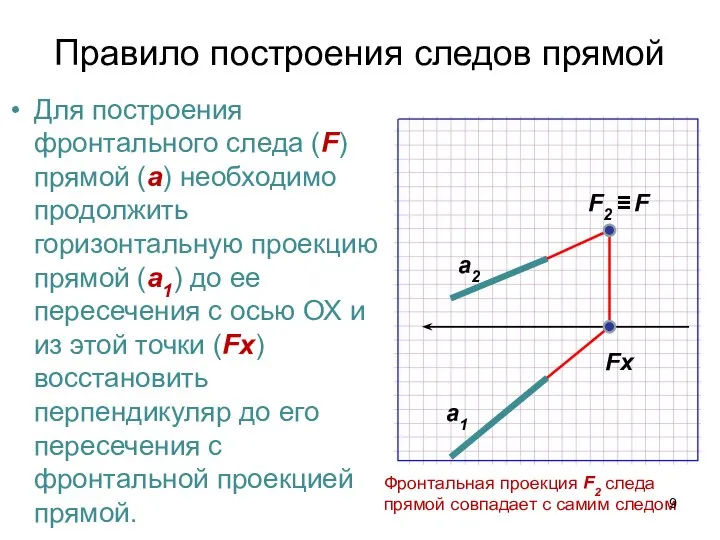
- 9. Правило построения следов прямой Для построения фронтального следа (F) прямой (а) необходимо продолжить горизонтальную проекцию прямой
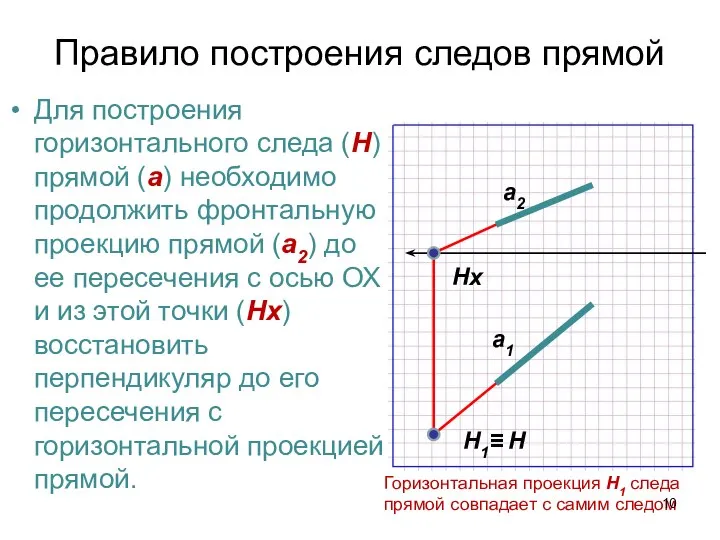
- 10. Правило построения следов прямой Для построения горизонтального следа (H) прямой (а) необходимо продолжить фронтальную проекцию прямой
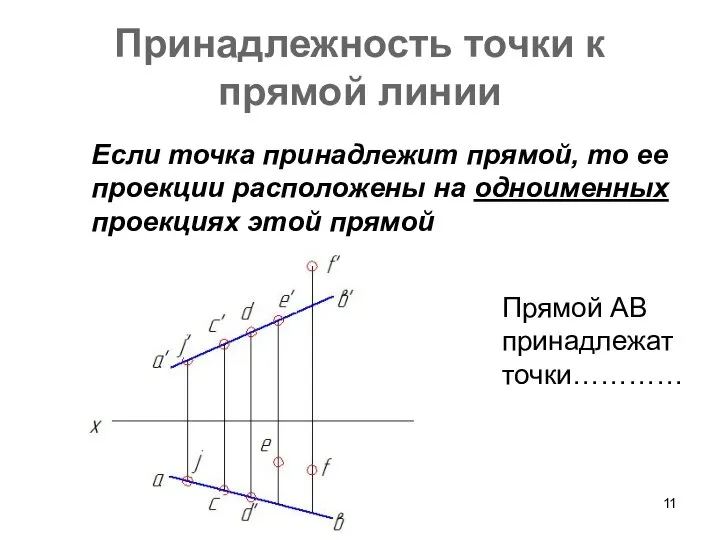
- 11. Принадлежность точки к прямой линии Если точка принадлежит прямой, то ее проекции расположены на одноименных проекциях
- 12. Положение прямой относительно плоскостей проекций: Параллельно – прямые уровня (горизонталь, фронталь, профильная прямая) Перпендикулярно – проецирующие
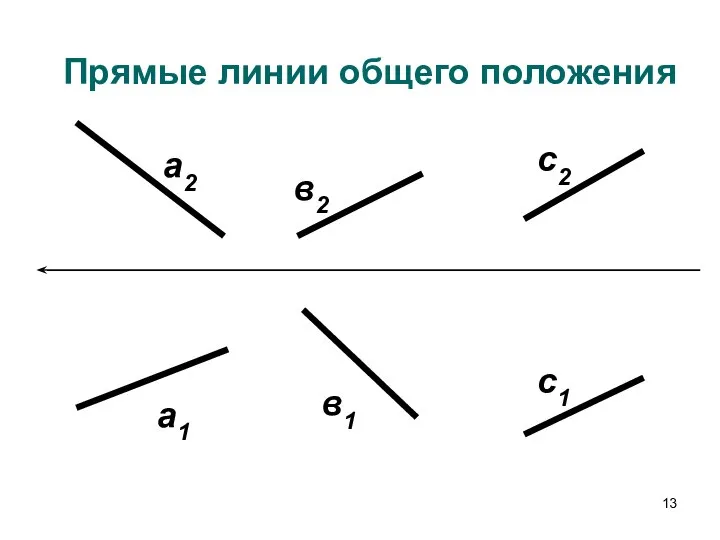
- 13. Прямые линии общего положения а2 в2 с2 а1 в1 с1
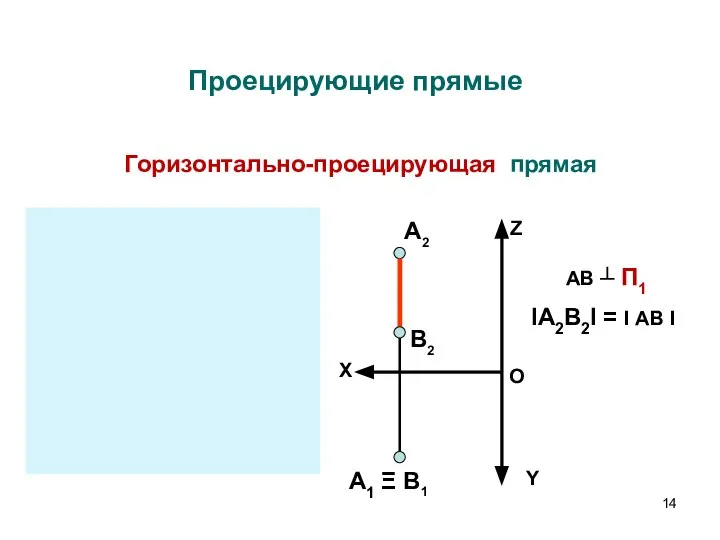
- 14. Проецирующие прямые Горизонтально-проецирующая прямая А B1 А1 B2 А2 B Ξ Z X Y Z X
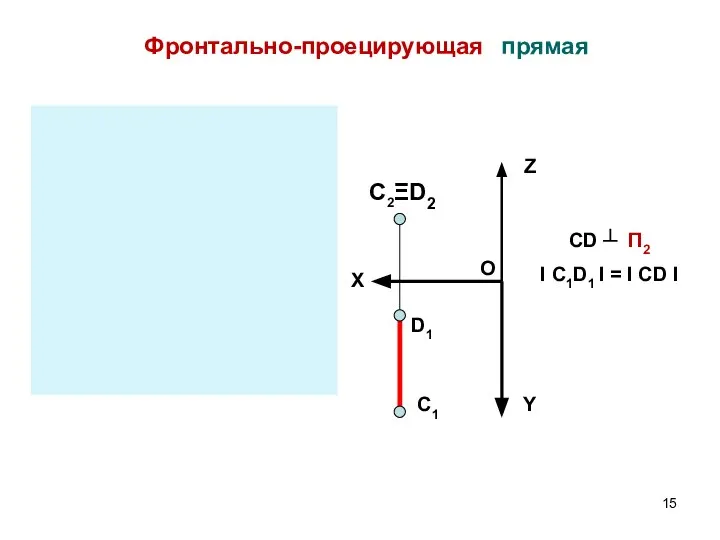
- 15. Фронтально-проецирующая прямая C Y Z X Y X Z D C1 C1 C2ΞD2 C2 Ξ D2
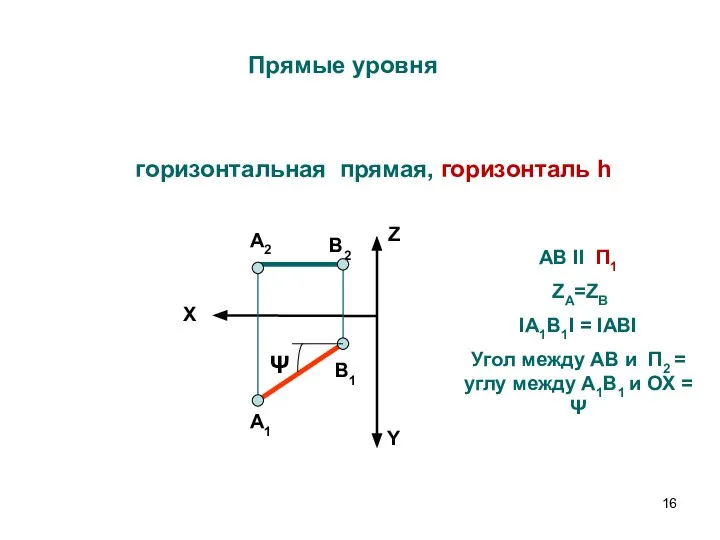
- 16. Прямые уровня горизонтальная прямая, горизонталь h X Z Y А2 А1 В2 В1 AВ II П1
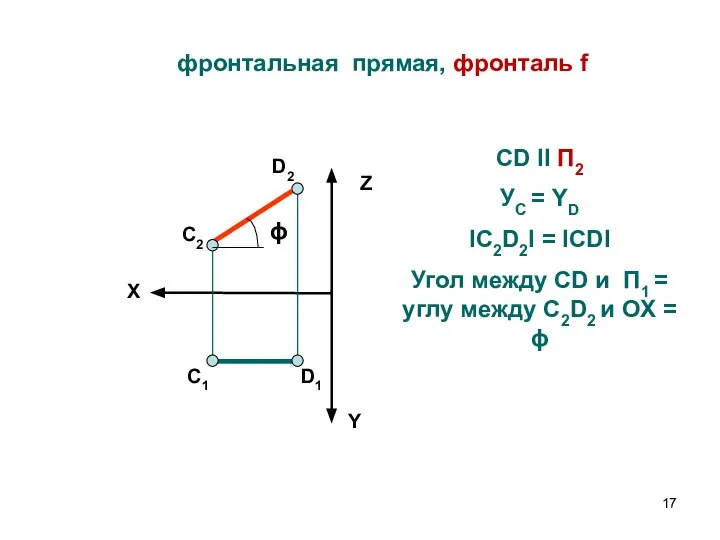
- 17. фронтальная прямая, фронталь f X Z Y C2 C1 D2 D1 CD II П2 УС =
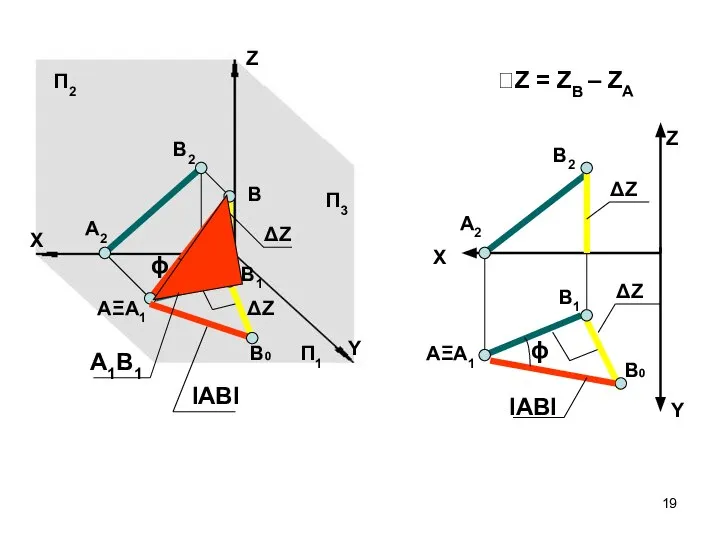
- 18. Определение натуральной величины отрезка прямой общего положения МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА ДЛИНА ОТРЕЗКА РАВНА ГИПОТЕНУЗЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА,
- 19. АΞА1 А2 Z Y X П1 П3 П2 В1 В2 Z Y В1 АΞА1 А2 В2
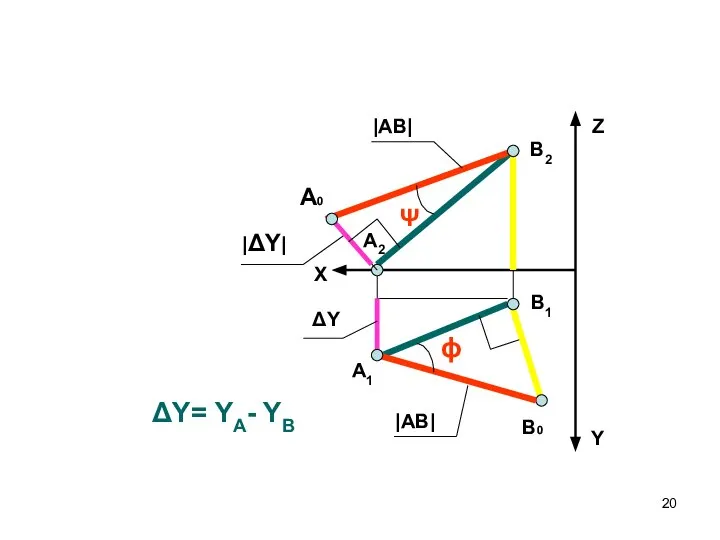
- 20. ΔY= YA- YB Z Y X В1 А2 В2 В0 А1 ΔY ϕ А0 Ψ |АВ|
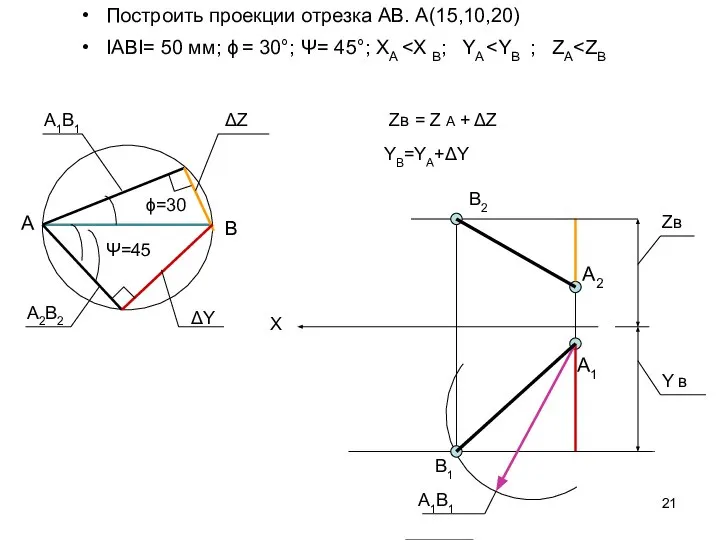
- 21. Построить проекции отрезка АВ. А(15,10,20) IАВI= 50 мм; ϕ = 30°; Ψ= 45°; XА X A2
- 22. Относительное положение прямых 1. Параллельно 2. Перпендикулярно 3. Пересекаться 4. Скрещиваться Прямые в пространстве могут быть
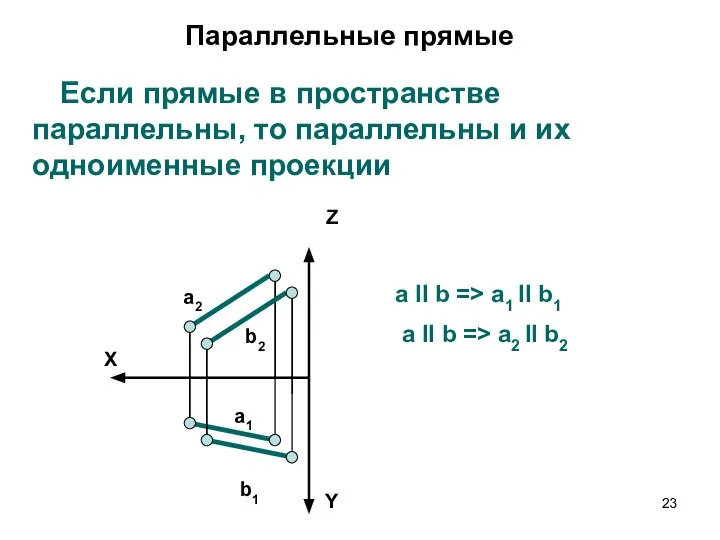
- 23. Параллельные прямые Если прямые в пространстве параллельны, то параллельны и их одноименные проекции X Z Y
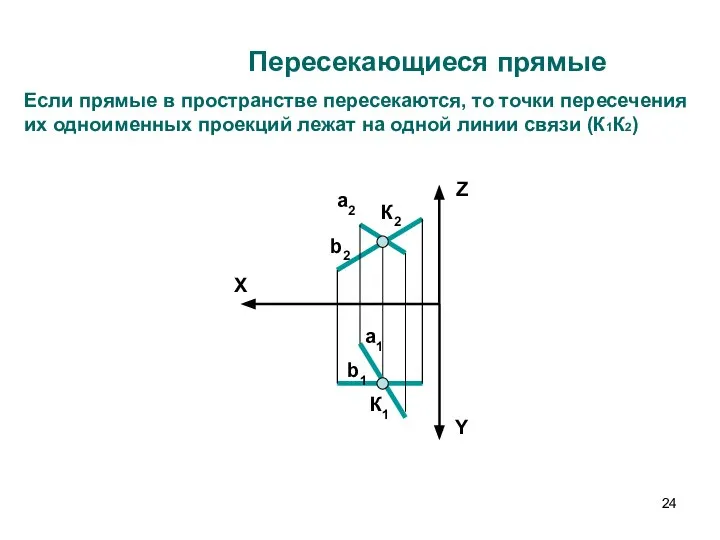
- 24. Пересекающиеся прямые X Z Y a2 К1 b2 b1 a1 К2 Если прямые в пространстве пересекаются,
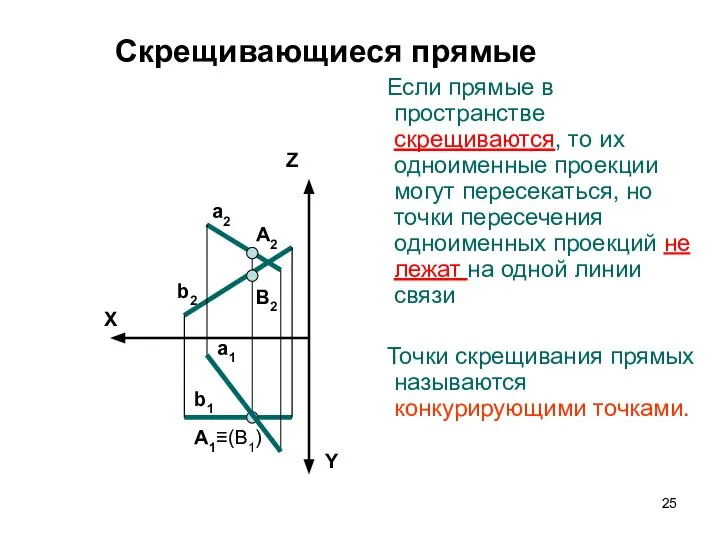
- 25. Скрещивающиеся прямые Если прямые в пространстве cкрещиваются, то их одноименные проекции могут пересекаться, но точки пересечения
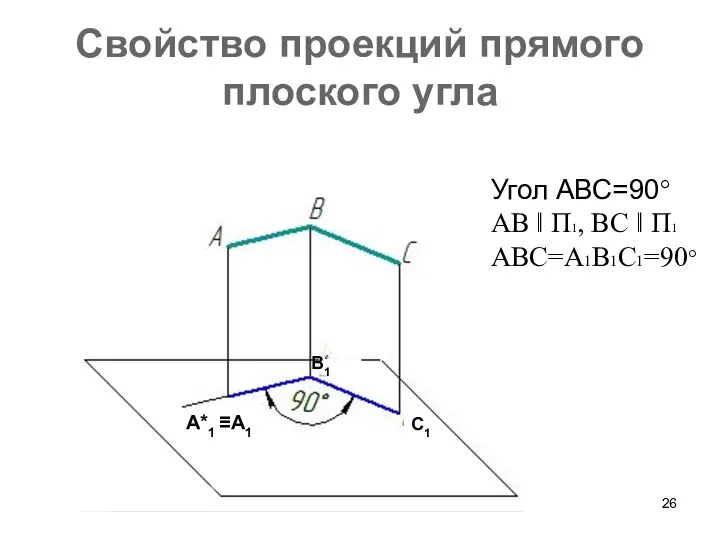
- 26. Свойство проекций прямого плоского угла Угол АВС=90° АВ ǁ П1, ВС ǁ П1 АВС=А1В1С1=90° А*1 ≡А1
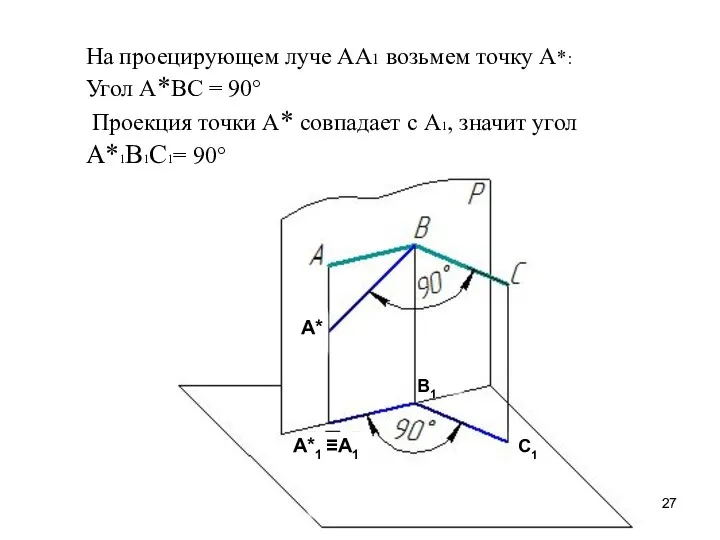
- 27. На проецирующем луче АА1 возьмем точку А*: Угол А*ВС = 90° Проекция точки А* совпадает с
- 28. Свойство проекций прямого плоского угла Если одна сторона прямого плоского угла параллельна плоскости проекций, то прямой
- 30. Скачать презентацию







 Сечение куба и сечение тетраэдра
Сечение куба и сечение тетраэдра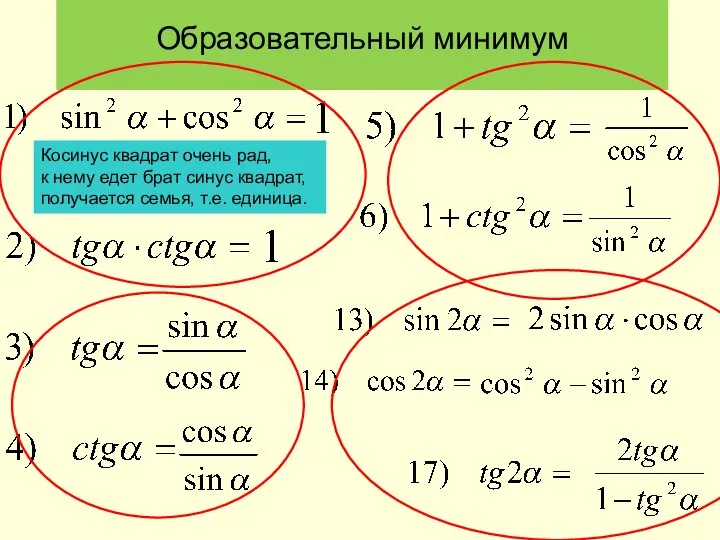 Образовательный минимум
Образовательный минимум Разложение многочлена на множители. Работа над ошибками
Разложение многочлена на множители. Работа над ошибками Путешествуем по странам Европы. 3 класс
Путешествуем по странам Европы. 3 класс Формулы нахождения объёма параллелеппипеда, объёма куба
Формулы нахождения объёма параллелеппипеда, объёма куба Теория вероятности. События и испытания
Теория вероятности. События и испытания Случаи вычитания 11-
Случаи вычитания 11- Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Презентация на тему Владимир Модестович Брадис
Презентация на тему Владимир Модестович Брадис  Окружность. Основные теоремы
Окружность. Основные теоремы Мультипликативная система индексов
Мультипликативная система индексов Решение текстовых задач арифметическим способом
Решение текстовых задач арифметическим способом Случаи вычитания 12-
Случаи вычитания 12- Площа прямокутника
Площа прямокутника Первообразная
Первообразная Сравнение обыкновенной дроби и десятичной
Сравнение обыкновенной дроби и десятичной Линейные измерения
Линейные измерения Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Деление одночлена на одночлен
Деление одночлена на одночлен Решение уравнений с помощью систем
Решение уравнений с помощью систем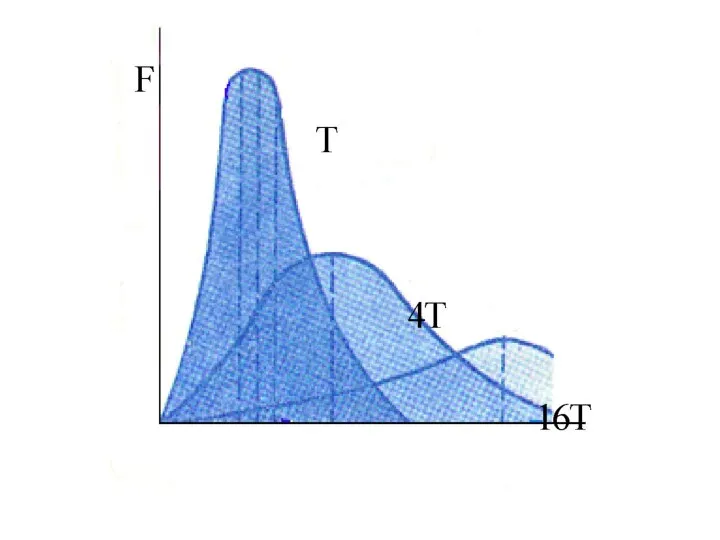 Функция распределения Максвелла
Функция распределения Максвелла Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Одночлен и его стандартный вид
Одночлен и его стандартный вид Презентация на тему Площадь круга
Презентация на тему Площадь круга  Пять великих математиков
Пять великих математиков Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Решение задач на параллельность прямых и плоскостей
Решение задач на параллельность прямых и плоскостей