Содержание
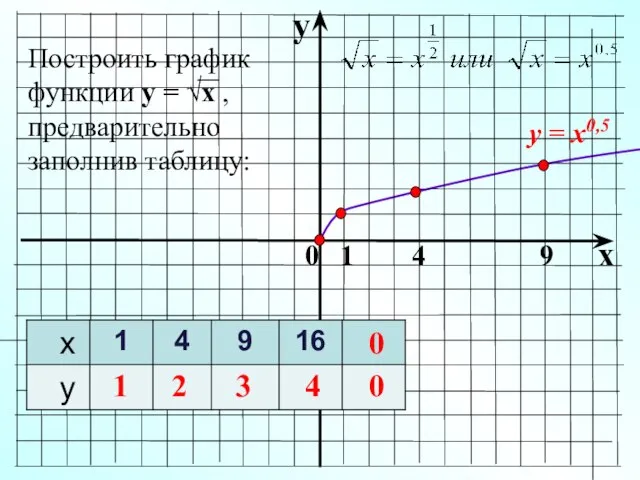
- 2. y x 0 1 4 9 у = х0,5 Построить график функции у = √х ,
- 3. Степенная функция Степенной функцией называется функция вида у = хр, где р – заданное действительное число
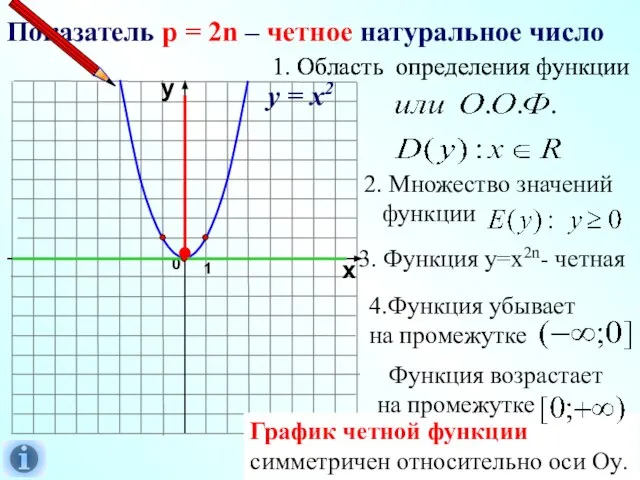
- 4. Показатель р = 2n – четное натуральное число 1 0 х у у = х2 3.
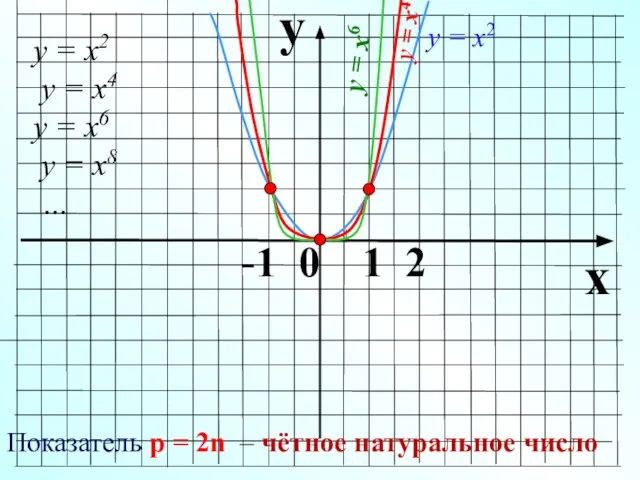
- 5. y x -1 0 1 2 у = х2 у = х6 у = х4 Показатель
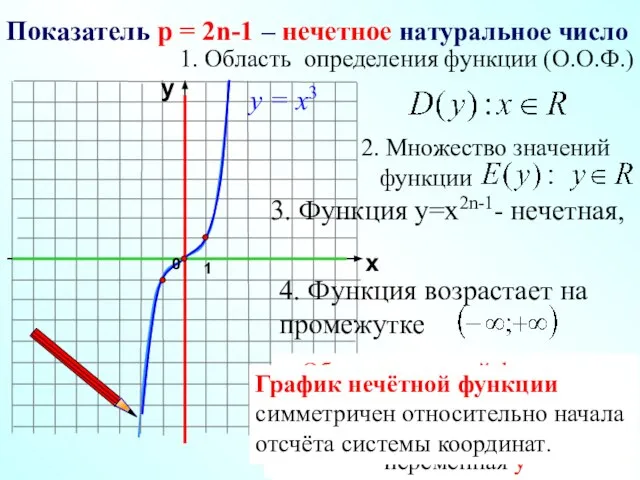
- 6. Показатель р = 2n-1 – нечетное натуральное число 1 х у у = х3 3. Функция
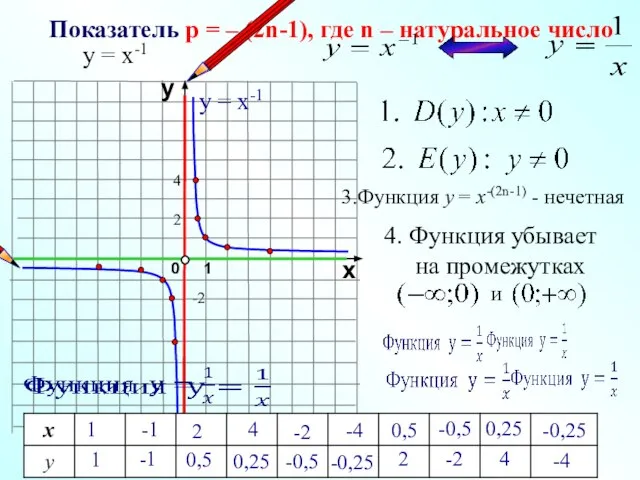
- 7. Показатель р = – (2n-1), где n – натуральное число у = х-1 , у =
- 8. Показатель р = – (2n-1), где n – натуральное число 1 0 х у 3.Функция у
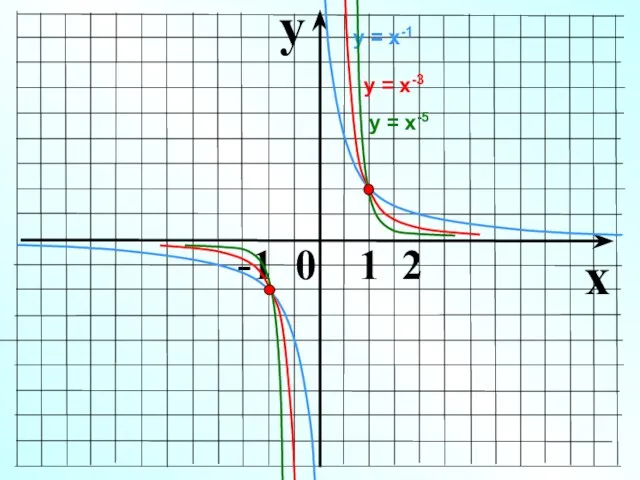
- 9. y x -1 0 1 2 у = х-1 у = х-3 у = х-5
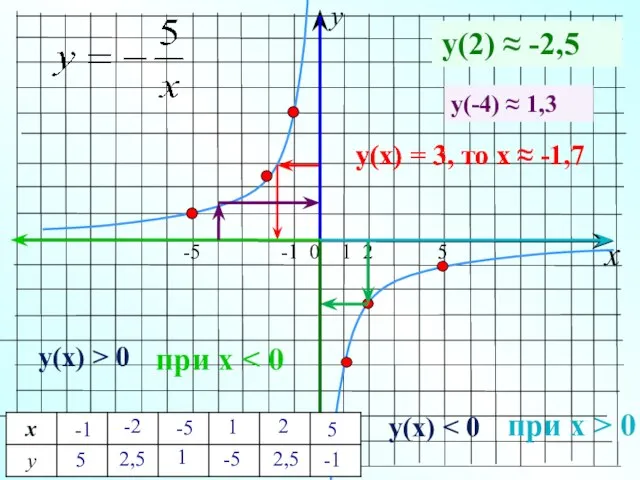
- 10. y x -5 -1 0 1 2 5 y(2) ≈ ? у(x) = 3, то х
- 11. Домашнее задание №125, №124
- 12. 2 занятие
- 13. 1 0 х у 1 1 -1 -1 2 0,5 4 0,25 -4 -0,25 -2 -0,5
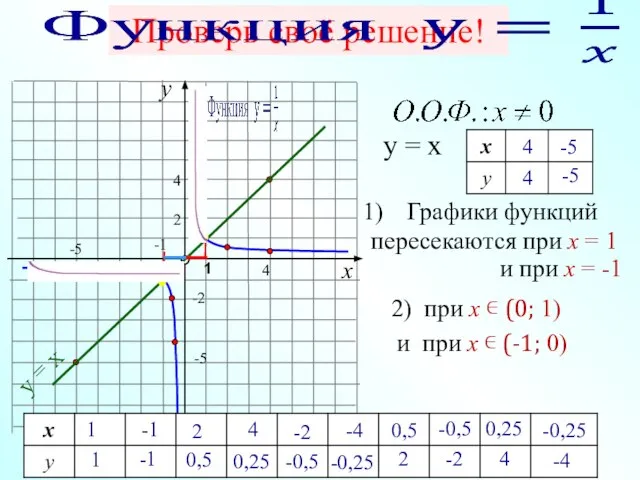
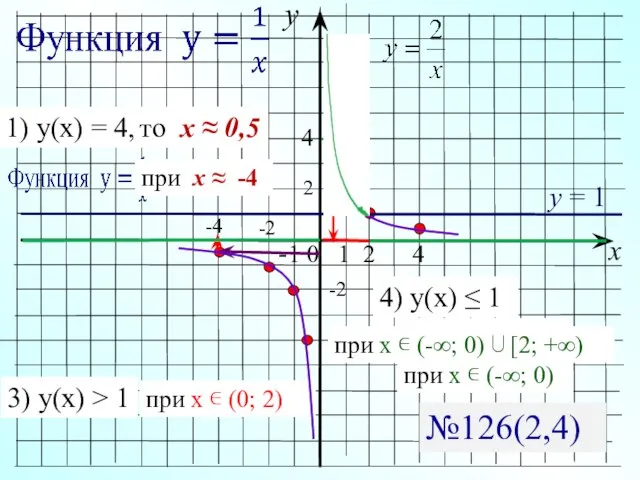
- 14. y x -1 0 1 2 4 1) у(x) = 4, 3) y(х) > 1 при
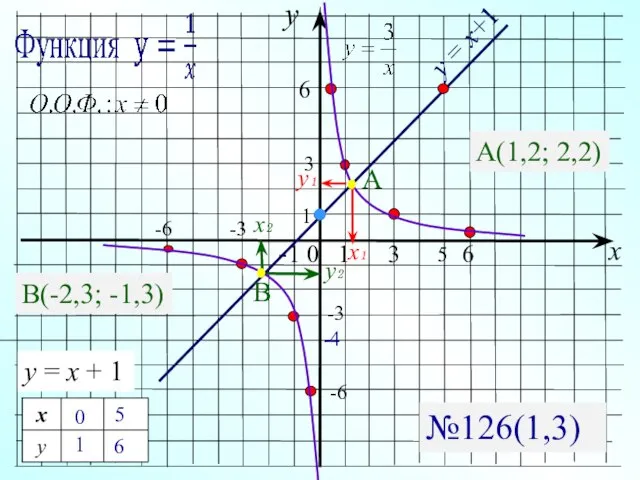
- 15. y x -1 0 1 3 6 6 3 -3 -3 -6 -6 у = х+1
- 16. №126(1) х ≠ 0 №126(3)
- 17. Домашнее задание №127(2), №126(2,4)
- 18. 3 занятие
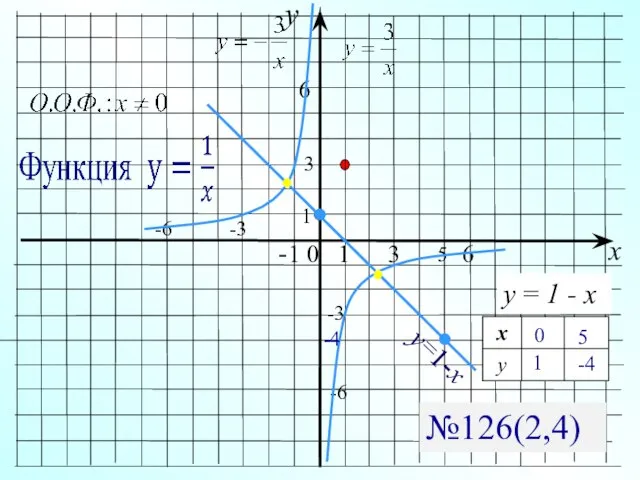
- 19. y x -1 0 1 3 6 6 3 -3 -3 -6 -6 №126(2,4) 5 1
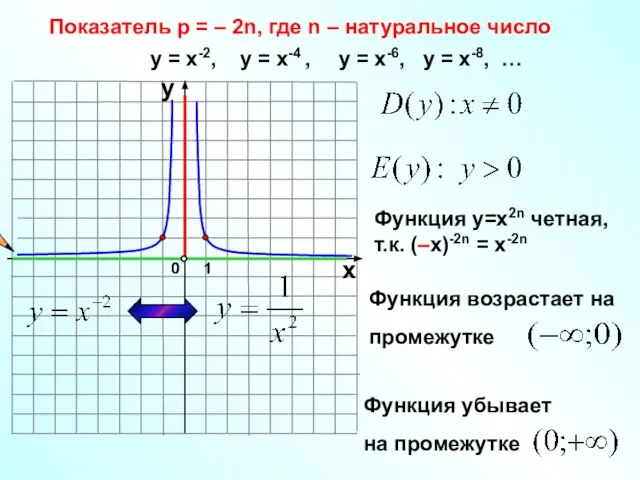
- 20. Показатель р = – 2n, где n – натуральное число 1 0 х у у =
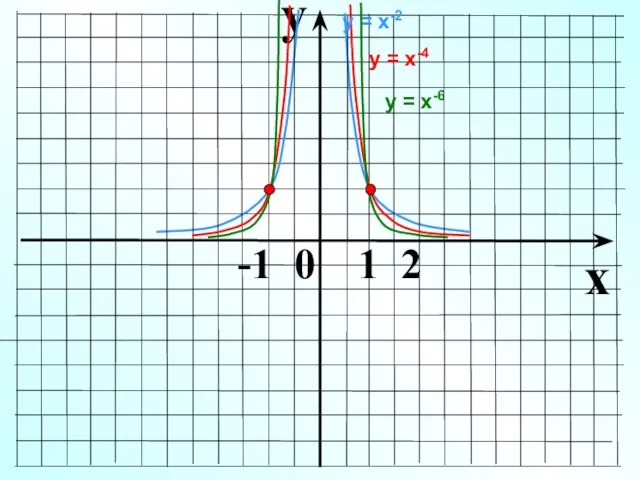
- 21. y x -1 0 1 2 у = х-4 у = х-2 у = х-6
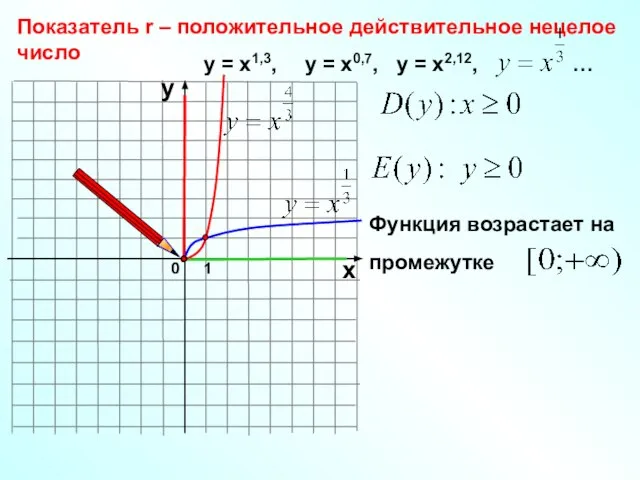
- 22. 0 Показатель r – положительное действительное нецелое число 1 х у у = х1,3, у =
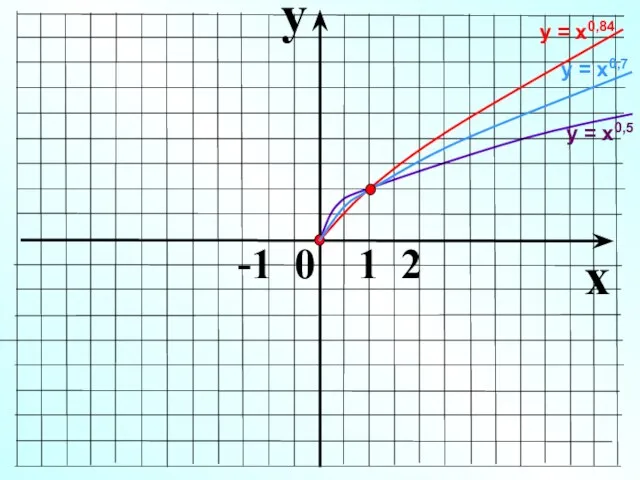
- 23. y x -1 0 1 2 у = х0,5
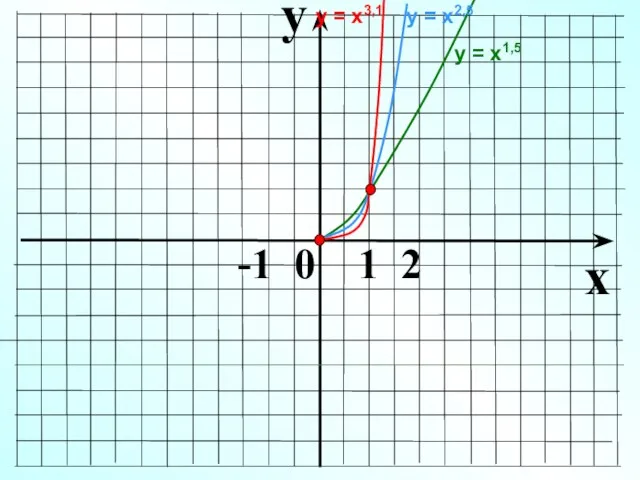
- 24. y x -1 0 1 2
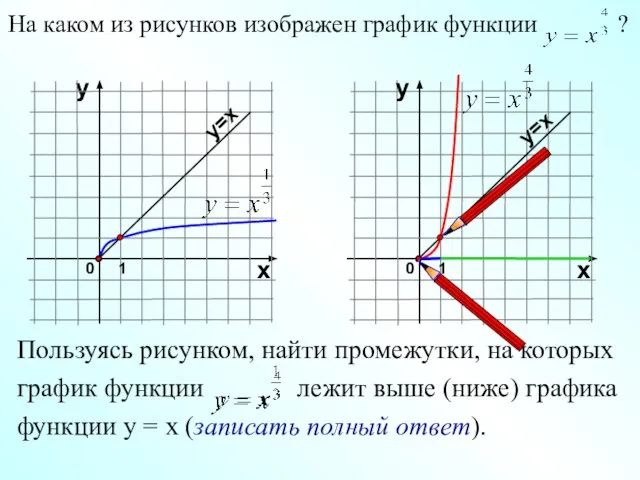
- 25. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х
- 27. Скачать презентацию







 Многоугольник. Урок 23
Многоугольник. Урок 23 Комбинаторика
Комбинаторика Решение логарифмических уравнений с применение свойств логарифма
Решение логарифмических уравнений с применение свойств логарифма Скалярное произведение векторов. тест
Скалярное произведение векторов. тест Вопросы при решении задач
Вопросы при решении задач Устный счёт. Вычисли наиболее лёгким способом
Устный счёт. Вычисли наиболее лёгким способом Вписанный угол
Вписанный угол Отображение плоскости на себя
Отображение плоскости на себя Понятие квадратного уравнения
Понятие квадратного уравнения Использование параллелограмма в жизни
Использование параллелограмма в жизни Решение линейных неравенств
Решение линейных неравенств Логарифмы вокруг нас
Логарифмы вокруг нас Письмо от президента Клуба серьёзных математиков
Письмо от президента Клуба серьёзных математиков Морской бой
Морской бой Понятие доли
Понятие доли Random module methods. Test
Random module methods. Test Полет на планету чисел. Открытый урок
Полет на планету чисел. Открытый урок Трансформация объема бытового предмета геометрическими телами
Трансформация объема бытового предмета геометрическими телами Тема: «Нумерация. Счёт предметов. Разряды»
Тема: «Нумерация. Счёт предметов. Разряды» Complete each of the following:
Complete each of the following: Производная сложной функции
Производная сложной функции 07_ ОТС_ Основы теории случайных процессов
07_ ОТС_ Основы теории случайных процессов Векторы в координатах
Векторы в координатах Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Методы измерений в квалиметрии
Методы измерений в квалиметрии Решение неполных квадратных уравнений
Решение неполных квадратных уравнений