Способы решения тригонометрических уравнений

Задачи урока:
Образовательная:
Изучить способы решения тригонометрических уравнений.
Организовать работу учащихся на уровне, соответствующем уровню сформированных знаний и умений.
Развивающая:
Развивать потребность в нахождении рациональных способов решения тригонометрических уравнений.
Воспитательная:
Способствовать развитию познавательного интереса учащихся к предмету, воздействуя на интерес старшеклассников к самопознанию.
Цель урока
Изучение способов решения тригонометрических уравнений

Желаю работать , желаю трудиться
Желаю успехов сегодня добиться
Ведь в будущем все это вам пригодится.
И легче в дальнейшем вам будет учиться
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»
Д. Пойа

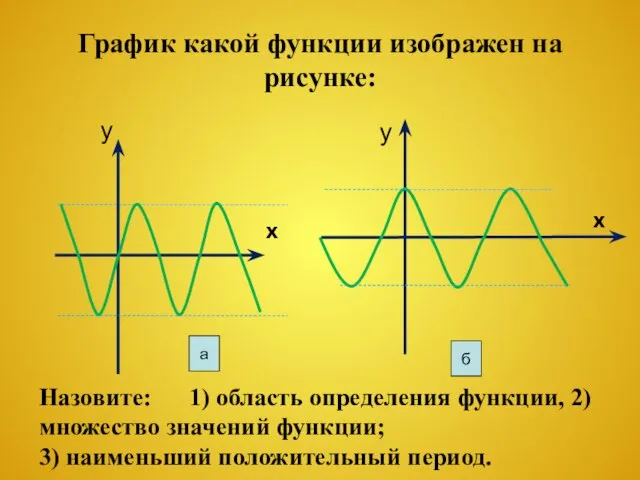
График какой функции изображен на рисунке:
Назовите: 1) область определения функции, 2)множество значений функции;
3) наименьший положительный период.
а
б
у
у
х
х

Общие формулы корней простейших тригонометрических уравнений.
1)
2)
3)
4)
а)
б)
в)
г)
tgx=a,
сtgx=a,
x =arcctg a +π n.
Поставьте в соответствие формулы уравнений и их решений.

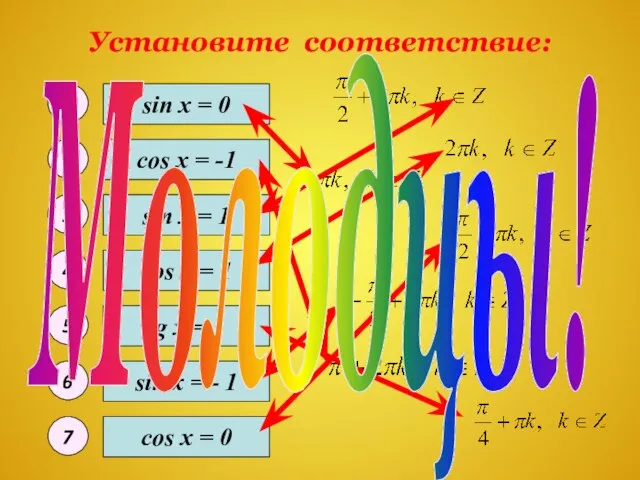
Установите соответствие:
sin x = 0
sin x = - 1
sin x = 1
cos x = 0
cos x = 1
tg x = 1
cos x = -1
1
2
3
4
5
6
7
Молодцы!

Реши простейшее
тригонометрическое уравнение

Изучение новой темы
Чтобы решить тригонометрическое уравнение, надо путем тождествен-ных преобразований привести его к простейшему тригонометрическому уравнению.

Способы решения тригонометрических уравнений
1. Тригонометрические уравнения, приводимые к алгеб-раическим уравнениям относительно одной тригоно-метрической функции
2. Тригонометрические уравнения, решаемые путем преобразований тригонометрическими формулами
3. Тригонометрические уравнения, решаемые путем понижения степени уравнения
4. Решение однородных тригонометрических уравнений
5.Тригонометрические уравнения, решаемые путем введения дополнительного аргумента

Рассмотрим пример.
1. Тригонометрические уравнения, приводимые к алгебраическим уравнениям относительно одной тригонометрической функции

Рассмотрим пример 2.

Реши тригонометрическое уравнение
1 вариант
2 вариант
взаимопроверка

проверка
1 вариант
2вариант

2. Тригонометрические уравнения, решаемые путем преобразований тригонометрическими формулами
Рассмотрим пример 1.

3. Тригонометрические уравнения, решаемые путем понижения степени уравнения

4. Решение однородных тригонометрических уравнений
Опр. Тригонометрическое уравнение называется однородным, если показатели степени слагаемых равны.

Применение знаний
Решить №116(а)
№ 117(б)
№ 122(в)

Д/з
п. 10. стр 68-75 учить
№ 116(б,г),
№ 117(а,в), 122(б)

Если «да» ─ , если «нет» +
cos ² x + sin ² x = 1, решением данного уравнения являются любые значения х.
Х = П/2 + 2Пn корень уравнения cos x = 0.
cos x = 1/2, его серия корней х = П/3 + 2 Пn
Метод решения уравнения 2cos ² x + 3cos x = 0 разложение на множители.
sin x + cos x = 1 - однородное уравнение.
Математика – мой любимый предмет.

«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию»
Я. А. Каменский