Слайд 2Цель урока. Обобщить понятие угла, дать понятие радианного измерения углов, научить учащихся

переводить углы из градусной меры в радианную и обратно.
Кратко познакомить учащихся с историей возникновения тригонометрии, развитие которой происходило в связи с необходимостью решения вычислительных задач, выдвигавшихся астрономией, географией, геодезией. Обратить внимание учащихся на тот факт, что академик Петербургской Академии наук Л.Эйлер окончательно разработал символику тригонометрии, которой пользуются и в наши дни. Радианная мера угла появилась уже в трудах И.Ньютона и Г.Лейбница, но вошла в науку и практику вычислений благодаря трудам Л.Эйлера.
Слайд 3Вид занятия. Обобщения и систематизации знаний.
Изучение материала.
- Понятие единичной окружности.
- Определение радиана..
-

Формулы перехода из радиан в градусы и обратно.
- Поворот точки вокруг начала координат.
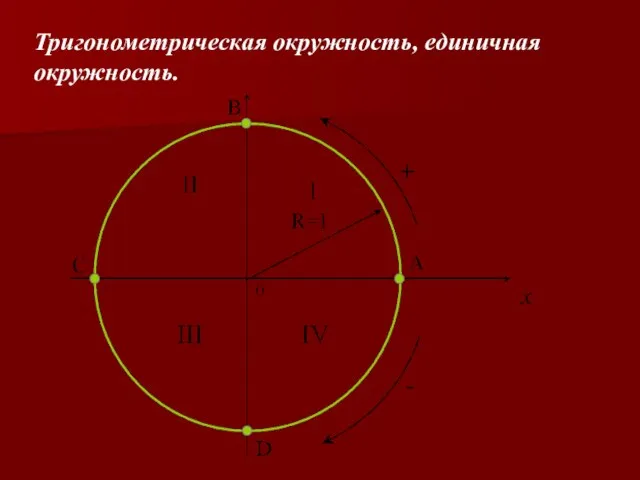
Слайд 4Тригонометрическая окружность, единичная окружность.
Слайд 5Градусная и радианная мера угла.
Углы измеряются градусной и радианной мерами.
Рассмотрим

единичную окружность.
Центральный угол, опирающийся на дугу, длина которой равна R окружности называется углом в 1 радиан
Слайд 6Выясним, сколько градусов соответствует углу в 1 радиан.
l=2πR – это длина дуги

окружности
πR – это длина дуги полуокружности, полуокружность соответствует центральному углу в 180°. Поэтому длина дуги длиной R стягивает угол в π раз меньший, т.е.
т.к π≈3,14, то 1 радиан = 57º 17' 45",
1º = 0, 017 радиана.
Слайд 7Для того, чтобы перейти от радианной меры к градусной нужно значение угла,

заданного в
радианной мере угла умножить на ,
например:
Слайд 82) Для того, чтобы перейти от градусной меры к радианной нужно значение

угла, заданного в
радианной мере угла умножить на ,
например:
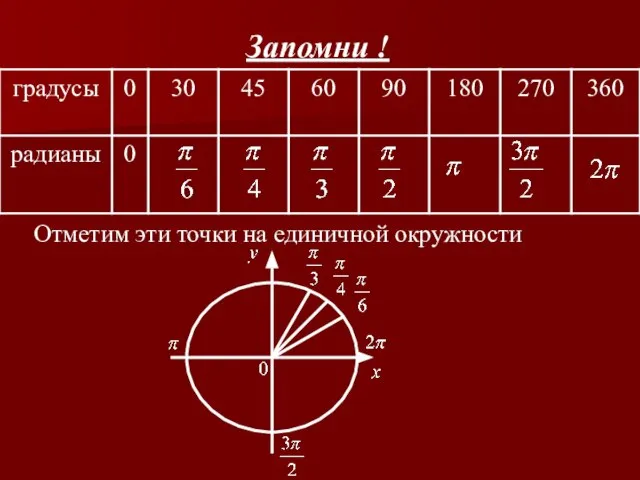
Слайд 9Запомни !
Отметим эти точки на единичной окружности
Слайд 11Поворот точки вокруг начала координат
1)Найти координаты точки единичной окружности, полученной поворотом точки

(1;0) на угол:
2)На единичной окружности построить точку, полученную поворотом точки с координатами (1;0) на заданный угол:
Слайд 12На какой угол можно повернуться еще, чтобы попасть в эти точки?

Слайд 13Вывод. Одной и той же точке М на единичной окружности соответствует бесконечное

множество действительных чисел α±2πn, где n – целое число.
Слайд 14Определение тригонометрических функций через стороны прямоугольного треугольника

Слайд 15История тригонометрии.
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
Впервые

способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.).
Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.
Слайд 16История тригонометрии.
История тригонометрии Зачатки тригонометрических познаний зародились в древности. На раннем этапе

тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.
Слайд 17История тригонометрии.
Если мы понимаем под синусом угла α в прямоугольном треугольнике ОВС

отношение катета ВС (линия синуса) к гипотенузе OC (т.е. радиусу единичной окружности), то в середине века термином «синус» обозначали саму линию синуса BC.
Слайд 18История тригонометрии.
Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л. Эйлера.

Слайд 19История тригонометрии.
Леонард Эйлер (1707-83), российский ученый — математик, механик, физик и

астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 в Россию. Был адъюнктом (1726), а в 1731-41 и с 1766 академиком Петербургской АН (в 1742-66 иностранный почетный член). В 1741-66 работал в Берлине, член Берлинской АН. Эйлер — ученый необычайной широты интересов и творческой продуктивности. Автор св. 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и других, оказавших значительное влияние на развитие науки.

















 Многогранники и их основные свойства
Многогранники и их основные свойства Формула сложных процентов в ЕГЭ. 11 класс
Формула сложных процентов в ЕГЭ. 11 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Практика. Дискретная математика
Практика. Дискретная математика Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Уравнение прямой
Уравнение прямой Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Координаты вектора
Координаты вектора Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Классификация многоугольников по числу углов
Классификация многоугольников по числу углов Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов  Переместительное свойство умножения
Переместительное свойство умножения Свойства умножения. 5 класс
Свойства умножения. 5 класс Математический турнир Умники и умницы
Математический турнир Умники и умницы Исследование операций. Принятие решений и неопределенность. Лекция 3
Исследование операций. Принятие решений и неопределенность. Лекция 3 11 клас призма
11 клас призма Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений Площадь треугольника
Площадь треугольника Параллельные прямые
Параллельные прямые Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Корень n-ой степени
Корень n-ой степени Шестое математическое действие
Шестое математическое действие Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование