- Главная
- Математика
- Погрешности измерений. Лекция 3

Содержание
- 2. Классификация погрешностей По способу числового выражения: абсолютные и относительные погрешности. В зависимости от источника возникновения: инструментальные,
- 3. Инструментальная погрешность измерения - составляющая погрешности измере-ния, обусловленная погрешностью применяемого средства измерений. Они принадлежат данному средству
- 4. Погрешность отсчитывания происходит от недостаточно точного отсчитывания показаний. Она обусловлена субъективными особенностями наблюдателя и вида отсчетного
- 5. По закономерностям проявления: систематические, прогрессирующие, случайные и грубые. Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся
- 6. Прогрессирующие погрешности — непрерывно возрастающие или убывающие погрешности. Как правило, вызываются процессами старения тех или иных
- 7. Поправка -значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Знак поправки
- 8. Вероятностный подход к описанию погрешностей Законы распределения случайных погрешностей. Случайные погрешности обнаруживают при проведении ряда измерений
- 9. При достаточно большом числе п одни и те же погрешности повторяются и можно установить относительную частоту
- 10. а б в Рис. 1 Если симметрична относительно точки Х, соответствующей вероятности 0,5, то распределение результатов
- 11. Дифференциальный закон распределения вероятностей для случайной погрешнос-ти с непрерывной и дифференцируемой функцией распределения называют функцию: Эта
- 12. Среднее квадратическое отклонение может быть выражено через случайные откло- нения результатов наблюдений Δi Чем меньше тем
- 13. Основными характеристиками законов распределения являются математическое ожидание и дисперсия. Математическое ожидание случайной величины – это значение,
- 14. Чем меньше дисперсия, тем точнее выполнены измерения. Дисперсия выражается в квадратных единицах измеряемой величины. В качестве
- 15. Затем вычисляют оценку значения средней квадратической погрешности для данного ряда измерений При достаточно большом числе измерений,
- 16. При оценке результатов измерений используется понятие максимальной или предель-ной допустимой погрешности, значение которой определяют в долях
- 17. В таблице приведены так называемые квантили распределения Стьюдента ⏐t(n)⏐Рд для числа измерений n = 2….20 и
- 19. Скачать презентацию
Слайд 2Классификация погрешностей
По способу числового выражения: абсолютные и относительные погрешности.
В зависимости от источника
Классификация погрешностей
По способу числового выражения: абсолютные и относительные погрешности.
В зависимости от источника

По закономерностям проявления: систематические, прогрессирующие, случайные и грубые.
Абсолютная погрешность измерения - погрешность измерения, выраженная в единицах измеряемой величины.
Абсолютная погрешность Δ – это разность между измеренным и истинным значениями измеряемой величины , на практике
Относительная погрешность измерения - погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины:
Слайд 3Инструментальная погрешность измерения - составляющая погрешности измере-ния, обусловленная погрешностью применяемого средства измерений.
Они
Инструментальная погрешность измерения - составляющая погрешности измере-ния, обусловленная погрешностью применяемого средства измерений.
Они

Эти погрешности обусловлены конструктивными и технологическими недостат-ками средств измерений, а также следствием их износа, старения или неисправности.
Погрешность метода измерений - составляющая погрешности измерений, обусловленная несовершенством принятого метода измерений.
Методические погрешности могут возникать из-за несовершенства физической модели явлений, положенных в основу метода измерений, неточности соотношений, используемых для нахождения оценки измеряемой величины, а также из-за несоответствия измеряемой величины и ее модели.
Пример: Измеряем падение напряжения на резисторе R2 вольтметром.
Отличительная особенность методических погрешностей в том, что они не могут быть указаны в паспорте прибора, а должны оцениваться самим экспериментатором при организации выбранной методики измерений, поэтому он обязан четко разли-чать фактически измеряемую им величину от подлежащей измерению.
Слайд 4Погрешность отсчитывания происходит от недостаточно точного отсчитывания показаний. Она обусловлена субъективными особенностями
Погрешность отсчитывания происходит от недостаточно точного отсчитывания показаний. Она обусловлена субъективными особенностями

Погрешности отсчитывания отсутствуют при использовании цифровых измерительных приборов.
Погрешность установки вызывается отклонением условий измерения от нор-мальных, т. е. условий, при которых производилась градуировка и поверка средств измерений. Сюда относится, например, погрешность от неправильной установки прибора в пространстве или его указателя на нулевую отметку, от изменения темпе-ратуры, напряжения питания и других влияющих величин.
Слайд 5По закономерностям проявления: систематические, прогрессирующие, случайные и грубые.
Систематическая погрешность измерения - составляющая
По закономерностям проявления: систематические, прогрессирующие, случайные и грубые.
Систематическая погрешность измерения - составляющая

Особенность систематических погрешностей состоит в том, что зависимость их от влияющих величин подчиняется определенному закону.
Наличие исключенных систематических погрешностей определяет правильность измерений, качество, отражающее близость к нулю систематических погрешностей.
Причины возникновения: несовершенство используемых средств и методов измерений, неправильная установка СИ, влияние внешних факторов на параметры СИ и на объект измерения и др.
В зависимости от характера изменения во времени разделяются на: постоянные, прогрессирующие, периодические и погрешности, изменяющиеся по сложному закону.
Постоянные - погрешности, которые в течение длительного времени, например, в течение времени выполнения всего ряда измерений, остаются постоянными (или неизменными). Они встречаются наиболее часто.
Примеры: погрешности, обусловленные неточностью подгонки значения меры, неправильной градуировкой шкалы прибора и др.
Слайд 6Прогрессирующие погрешности — непрерывно возрастающие или убывающие погрешности.
Как правило, вызываются процессами старения
Прогрессирующие погрешности — непрерывно возрастающие или убывающие погрешности.
Как правило, вызываются процессами старения

Пример: погрешности вследствие износа измерительных наконечников, контакти-рующих с деталью при контроле ее прибором активного контроля.
Могут быть скорректированы путем введения поправки лишь в заданный момент времени, а далее вновь непредсказуемо возрастают или убывают.
Периодические погрешности — погрешности, значение которых является пери-одической функцией времени или перемещения указателя измерительного прибора.
Пример: погрешность возникающая при круговой шкале, если её ось не совпадает с осью вращения.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совмес-тного действия нескольких систематических погрешностей.
В зависимости от характера изменения по диапазону измерений систематические погрешности подразделяются на постоянные и пропорциональные.
Пропорциональные погрешности - погрешности, значение которых пропорцио-нально значению измеряемой величины.
Слайд 7Поправка -значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих
Поправка -значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих

Знак поправки противоположен знаку погрешности
Различают: неисправленный и исправленный результат измерения.
Неисправленный результат измерения - значение величины, полученное при изме-рении до введения в него поправок, учитывающих систематические погрешности.
Исправленный результат измерения - полученное при измерении значение вели-чины и уточненное путем введения в него необходимых поправок на действие систе-матических погрешностей.
Случайная погрешность измерения - составляющая погрешности измерения, изме-няющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных в определенных условиях.
Обнаруживаются случайные погрешности при многократных измерениях одной и той же величины (отдельные измерения в этом случае называются наблюдением) од-ними и теми же средствами измерения в одинаковых условиях одним и тем же наблю-дателем, т. е. при равноточных (равнорассеянных) измерениях. Влияние случайных погрешностей на результат измерения учитывается методами математической ста-тистики и теории вероятности.
Грубая погрешность измерений – случайная погрешность измерений, существенно превышающие ожидаемые при данных условиях погрешности.
Как правило, результаты измерений, содержащие грубые погрешности, не принима-ются во внимание, поэтому грубые погрешности мало влияют на точность измерения.
Погрешность измерения равна сумме случайной и систематической погрешностей.
Слайд 8Вероятностный подход к описанию погрешностей
Законы распределения случайных погрешностей.
Случайные погрешности обнаруживают при проведении
Вероятностный подход к описанию погрешностей
Законы распределения случайных погрешностей.
Случайные погрешности обнаруживают при проведении

Пусть величину Х измеряли п раз и наблюдали при этом значения х1, х2, х3,…, хn. Случайная абсолютная погрешность единичного измерения будет равна:
Распределение результатов измерений
Слайд 9При достаточно большом числе п одни и те же погрешности повторяются и
При достаточно большом числе п одни и те же погрешности повторяются и

Частость - отношение числа полученных одинаковых данных mi к общему числу проведенных измерений п.
При продолжении измерений величины Х эта частота не изменится, поэтому ее можно считать вероятностью появления погрешности при данных измерениях:
Статистическая зависимость вероятности появления случайных погрешностей от их значения называется законом распределения погрешностей или законом распреде-ления вероятности.
Различают два вида описания законов распределения: интегральный и дифференциальный.
Интегральный закон, или функция распределения вероятностей случайной погрешности Δi в i-м опыте - функция, значение которой для каждого Δ определяется вероятностью события , заключающегося в том, что случайная погрешность Δi принимает значения, меньше некоторого значения Δ, т. е. функцию .
Эта функция при изменении Δ от -∞ до +∞ принимает значения от 0 до 1 и является неубывающей (рис. 1а). Она существует для всех случайных величин как дискретных, так и непрерывных.
Слайд 10
а б в
Рис. 1
Если симметрична относительно точки
а б в
Рис. 1
Если симметрична относительно точки
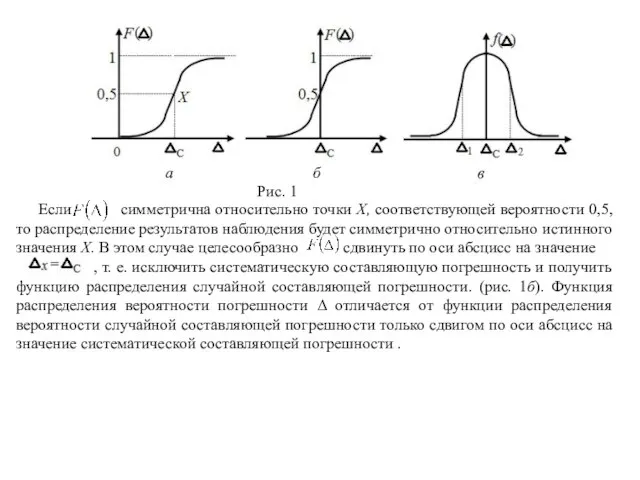
, т. е. исключить систематическую составляющую погрешность и получить функцию распределения случайной составляющей погрешности. (рис. 1б). Функция распределения вероятности погрешности Δ отличается от функции распределения вероятности случайной составляющей погрешности только сдвигом по оси абсцисс на значение систематической составляющей погрешности .
Слайд 11Дифференциальный закон распределения вероятностей для случайной погрешнос-ти с непрерывной и дифференцируемой функцией
Дифференциальный закон распределения вероятностей для случайной погрешнос-ти с непрерывной и дифференцируемой функцией

Эта зависимость представляется плотностью распределения вероятностей. Ее график может иметь различную форму в зависимости от закона распределения пог-решностей. Для (рис. 1б) кривая распределения имеет форму, близкую к форме колокола (рис. 1в).
Значение есть элемент вероятности, равный площади прямоугольника с основанием и абсциссами Δ1 , Δ2, называемыми квантилями.
Площадь под кривой равна единице и отражает вероятность всех возможных событий.
В практике измерений одним из наиболее распространенных законов распределе-ния случайных погрешностей является нормальный закон (Гаусса):
- плотность вероятности случайной погрешности;
-среднее квадратическое отклонение.
Слайд 12Среднее квадратическое отклонение может быть выражено через случайные откло- нения результатов наблюдений
Среднее квадратическое отклонение может быть выражено через случайные откло- нения результатов наблюдений
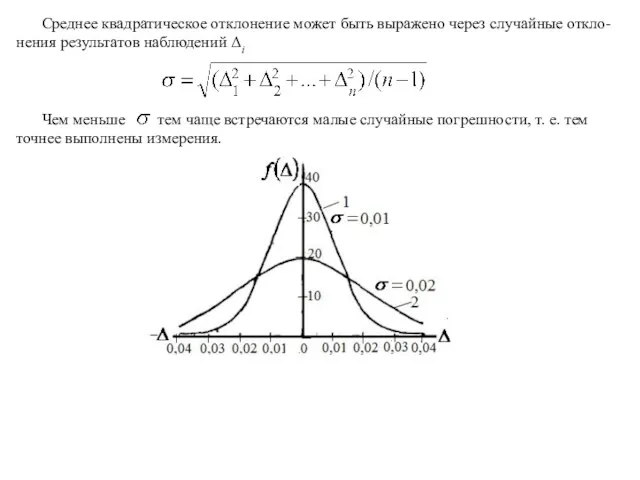
Чем меньше тем чаще встречаются малые случайные погрешности, т. е. тем точнее выполнены измерения.
Слайд 13Основными характеристиками законов распределения являются математическое ожидание и дисперсия.
Математическое ожидание случайной величины
Основными характеристиками законов распределения являются математическое ожидание и дисперсия.
Математическое ожидание случайной величины

Для непрерывных случайных величин
f(x) – функция плотности вероятности.
Для нормального распределения случайных погрешностей математическое ожида-ние равно нулю. Если же рассматривать нормальное распределение результатов, то ма-тематическое ожидание будет соответствовать истинному значению измеряемой величины Х.
Дисперсия ряда наблюдений характеризует степень рассеивания (разброса) результатов отдельных наблюдений вокруг математического ожидания:
Слайд 14Чем меньше дисперсия, тем точнее выполнены измерения. Дисперсия выражается в квадратных единицах
Чем меньше дисперсия, тем точнее выполнены измерения. Дисперсия выражается в квадратных единицах

При проведении n измерений погрешность будет различной
где - погрешность i-го измерения; -результат i-го измерения.
При практических расчетах используется оценка истинного значения - среднее арифметическое значение ряда измерений:
Отклонение результата каждого измерения от среднего значения определяется как:
vi – отклонение результата единичного измерения от среднего значения.
Слайд 15Затем вычисляют оценку значения средней квадратической погрешности для данного ряда измерений
При
Затем вычисляют оценку значения средней квадратической погрешности для данного ряда измерений
При

Так как среднее арифметическое значение также является случайной величиной, введено понятие среднеквадратического отклонения среднего арифметического значения .
Слайд 16При оценке результатов измерений используется понятие максимальной или предель-ной допустимой погрешности, значение
При оценке результатов измерений используется понятие максимальной или предель-ной допустимой погрешности, значение

Понятия доверительной вероятности и доверительного интервала.
Пусть РД есть вероятность того, что отличается от Х не более чем на Δ, т. е.
Вероятность РД называется доверительной вероятностью, а интервал значений изме-ряемой величины от до - доверительным интервалом.
Это означает что доверительный интервал от до заключает в себе истинное значение Х.
Для достаточно полной характеристики случайной погрешности надо располагать двумя числами – доверительной вероятностью и соответствующим ей доверительным интервалом.
Если закон распределения вероятностей погрешностей известен, то по заданной дове-рительной вероятности можно определить доверительный интервал. При достаточно большом числе измерений часто используется нормальный закон. При небольшом числе измерений, результаты которых принадлежат нормальному распределению, следует ис-пользовать распределение Стьюдента. Это распределение имеет плотность вероятнос-тей, практически совпадающую с нормальной при больших п, но значительно отличающуюся от нормальной при малых п.
Слайд 17В таблице приведены так называемые квантили распределения Стьюдента ⏐t(n)⏐Рд для числа измерений
В таблице приведены так называемые квантили распределения Стьюдента ⏐t(n)⏐Рд для числа измерений
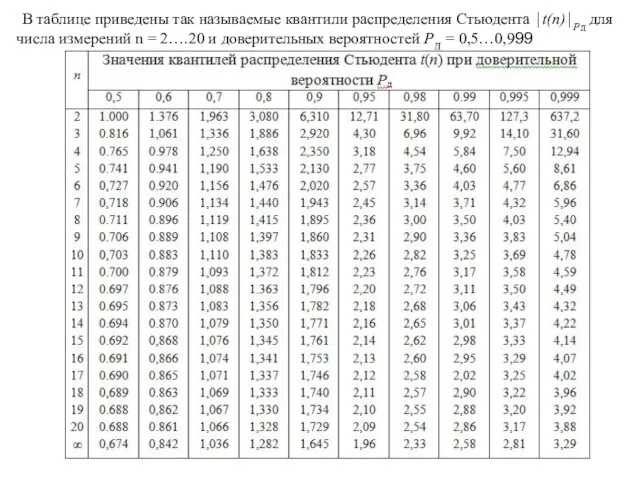
.
 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему Нестандартные задачи для шестиклассников
Презентация на тему Нестандартные задачи для шестиклассников  Презентация на тему Графики тригонометрических функций
Презентация на тему Графики тригонометрических функций  Множества и операции над ними
Множества и операции над ними Нормальное распределение
Нормальное распределение Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Умножение натуральных чисел
Умножение натуральных чисел Занятие математического кружка по теме Площадь. 5 класс
Занятие математического кружка по теме Площадь. 5 класс График функции
График функции Графовые модели. Основные понятия. Принцип планирования многошаговых процессов
Графовые модели. Основные понятия. Принцип планирования многошаговых процессов Уравнение прямой на координатной плоскости
Уравнение прямой на координатной плоскости Элементы теории вероятности
Элементы теории вероятности Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений График функции. Тест, 1-6 варианты
График функции. Тест, 1-6 варианты Тригонометрические и Логарифмические уравнения. Объёмы тел
Тригонометрические и Логарифмические уравнения. Объёмы тел Аналитическая геометрия
Аналитическая геометрия Приёмы устных вычислений вида 260+310 670-140
Приёмы устных вычислений вида 260+310 670-140 Решаем задачу
Решаем задачу Аксиомы стереометрии
Аксиомы стереометрии Системы линейных уравнений
Системы линейных уравнений Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Презентация на тему Логарифмы. Применение логарифмов
Презентация на тему Логарифмы. Применение логарифмов  Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график Математика. Числа до 20
Математика. Числа до 20 Презентация на тему Симметрия вокруг нас
Презентация на тему Симметрия вокруг нас  Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс
Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс  Последовательности
Последовательности Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью