Шар. Сфера

Шар – это…
…тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.

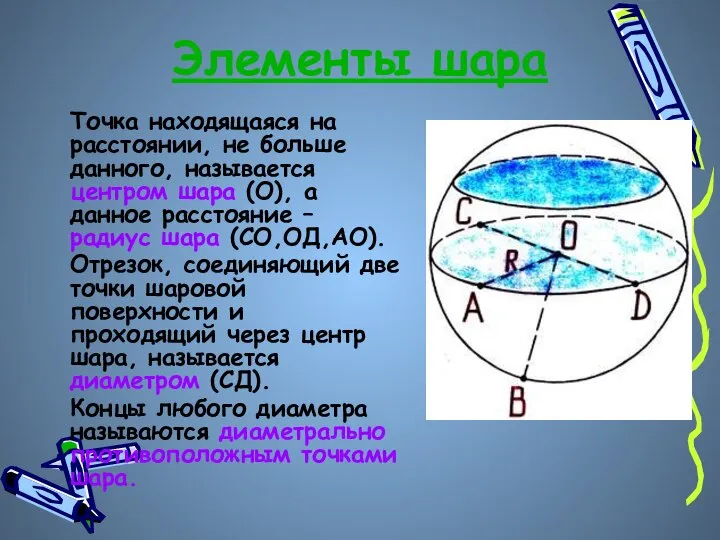
Элементы шара
Точка находящаяся на расстоянии, не больше данного, называется центром шара (О), а данное расстояние – радиус шара (СО,ОД,АО).
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром (СД).
Концы любого диаметра называются диаметрально противоположным точками шара.

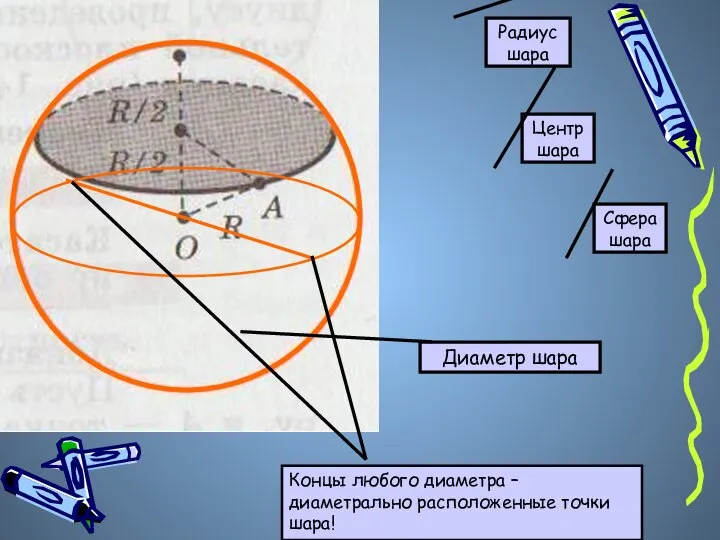
Центр
шара
Радиус шара
Сфера шара
Диаметр шара

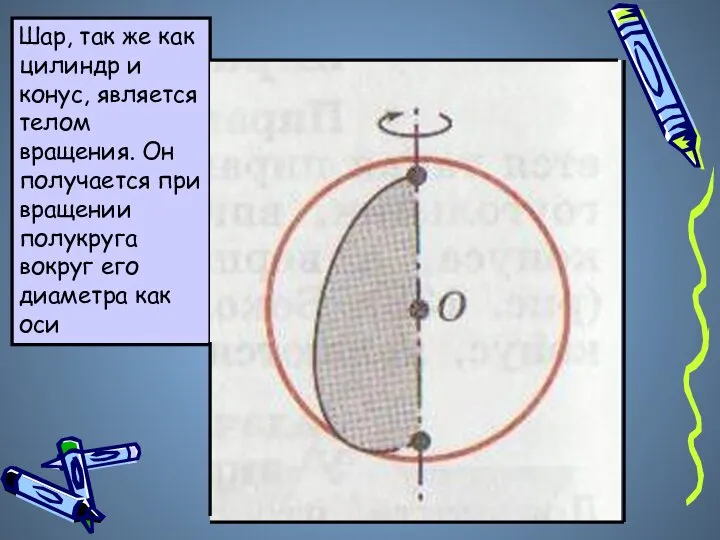
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси

Сечение шара плоскостью
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

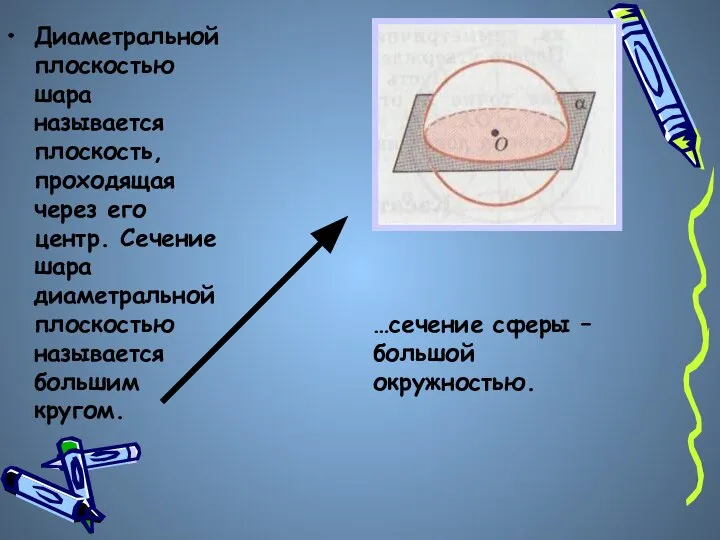
Диаметральной плоскостью шара называется плоскость, проходящая через его центр. Сечение шара диаметральной плоскостью называется большим кругом.
…сечение сферы – большой окружностью.

Симметрия шара…
Любая диаметральная плоскость шара является плоскостью его симметрии. Центр шара является его центром симметрии.

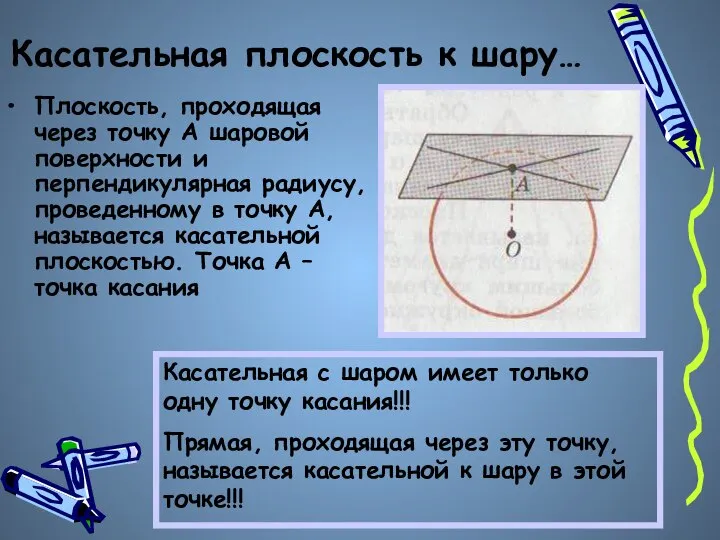
Касательная плоскость к шару…
Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А – точка касания
Касательная с шаром имеет только одну точку касания!!!
Прямая, проходящая через эту точку, называется касательной к шару в этой точке!!!

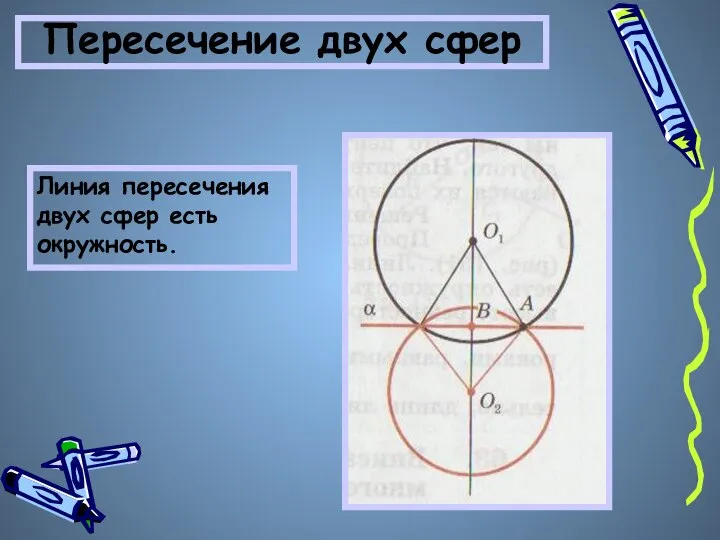
Пересечение двух сфер
Линия пересечения двух сфер есть окружность.