Содержание
- 2. Построения циркулем и линейкой Тимербаева Н.В., кпн, доцент кафедры теории и технологий преподавания математики и информатики
- 3. В задачах на построение на плоскости фигуру F мы считаем построенной, если эта фигура, изображена (начерчена).
- 4. Аксиомы конструктивной геометрии А1. Каждая данная фигура F построена. А2. Если построены фигуры F1 и F2,
- 5. В классической теории геометрических построений на плоскости (и в школьном курсе геометрии) допустимыми средствами построения являются
- 6. Простейшие построения П1. Построить отрезок АВ, если А и В построены. Решение задачи на построение мы
- 7. Перечислим эти, так называемые, основные (элементарные) построения, которые наиболее часто встречаются в практике решения задач на
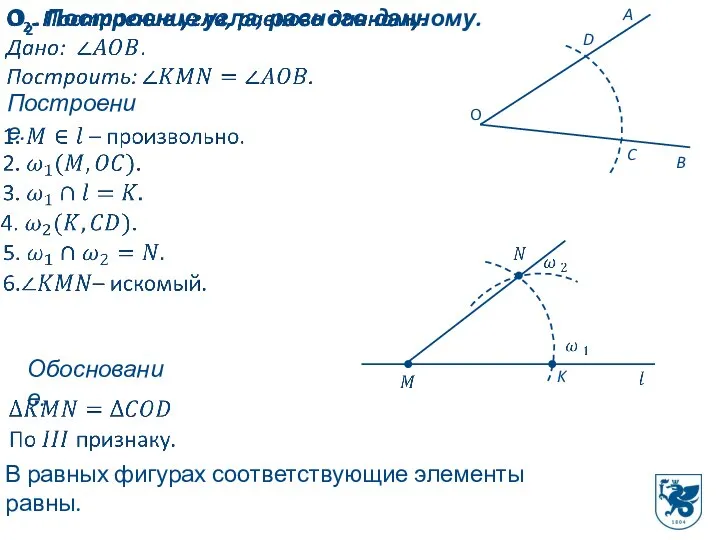
- 8. О2. Построение угла, равного данному. Построение. C D K Обоснование. В равных фигурах соответствующие элементы равны.
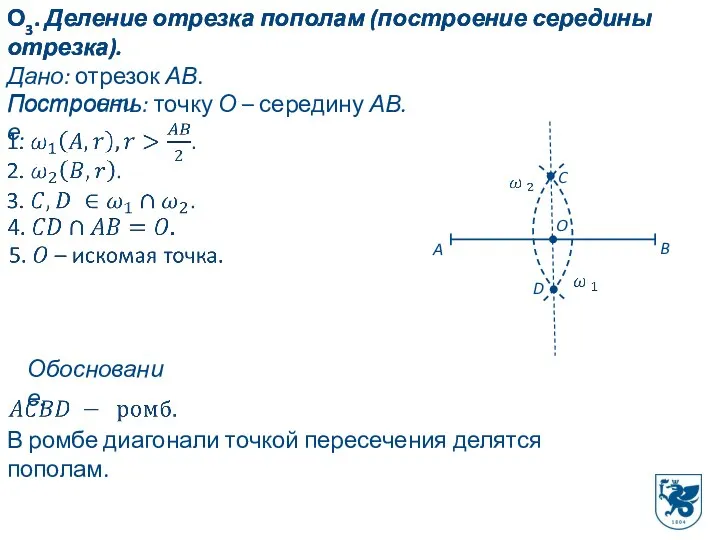
- 9. О3. Деление отрезка пополам (построение середины отрезка). О3. Деление отрезка пополам (построение середины отрезка). Дано: отрезок
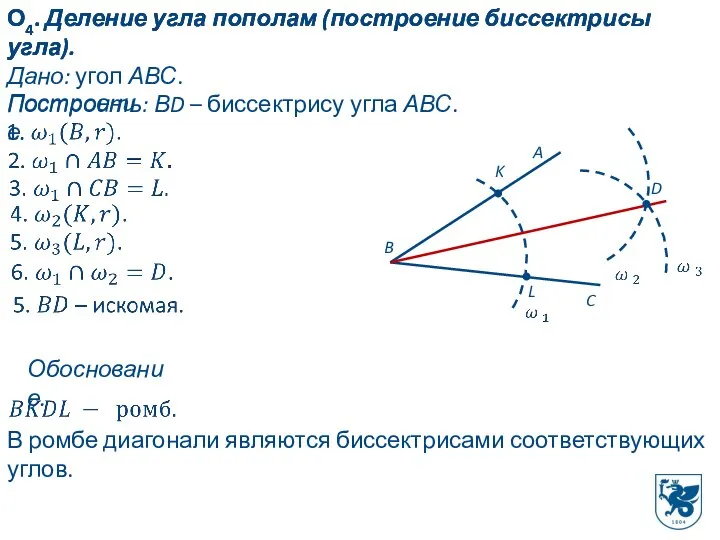
- 10. О4. Деление угла пополам (построение биссектрисы угла). О4. Деление угла пополам (построение биссектрисы угла). Дано: угол
- 11. О5. Построение перпендикуляра к данной прямой, проходящей через данную точку. B C A a Построение. D
- 12. А a B C Построение. D Обоснование. В ромбе диагонали взаимно-перпендикулярны.
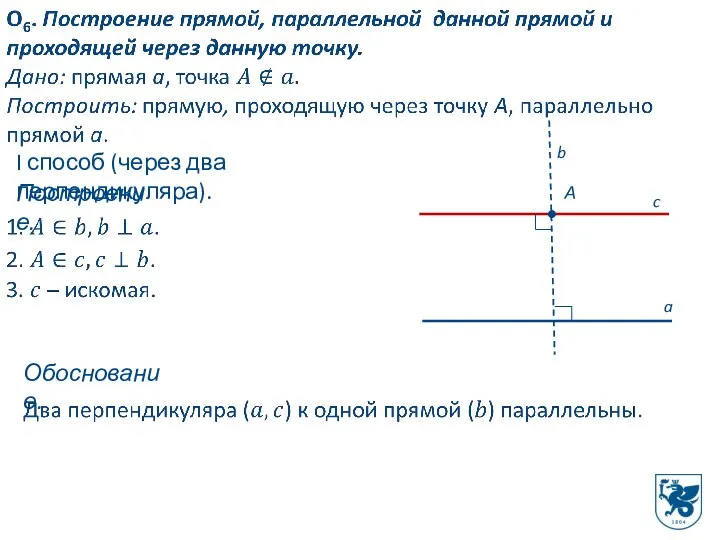
- 13. I способ (через два перпендикуляра). Построение. a А b c Обоснование.
- 14. II способ (через параллелограмм). a А B C D Обоснование. По признаку: четырехугольник, в котором стороны
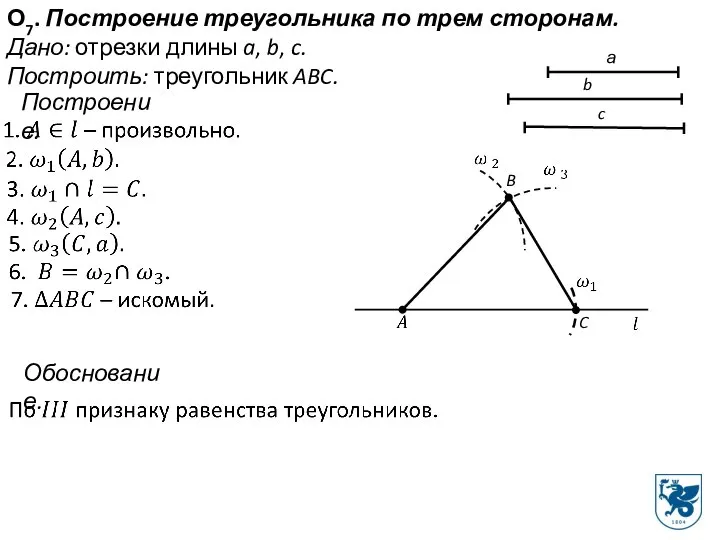
- 15. О7. Построение треугольника по трем сторонам. Дано: отрезки длины a, b, c. Построить: треугольник ABC. Построение.
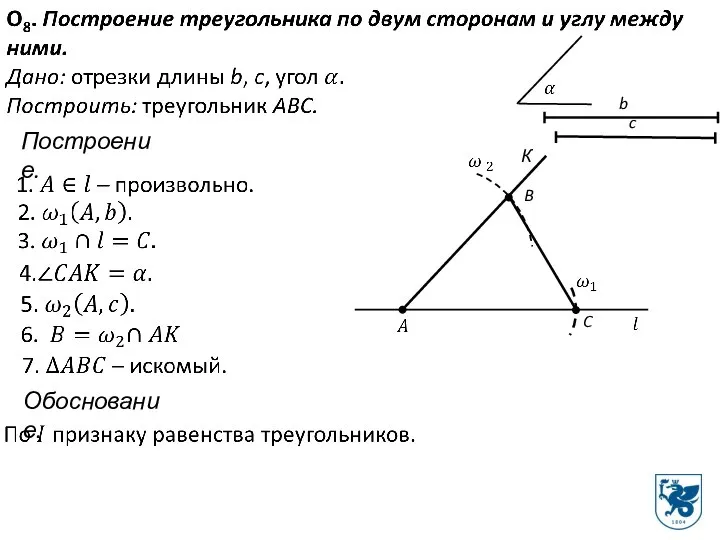
- 16. Построение. C К B Обоснование.
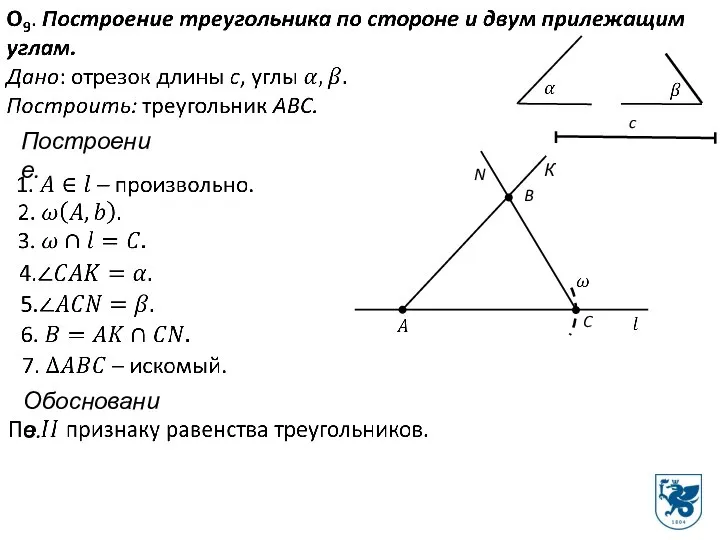
- 17. Построение. C К B N Обоснование.
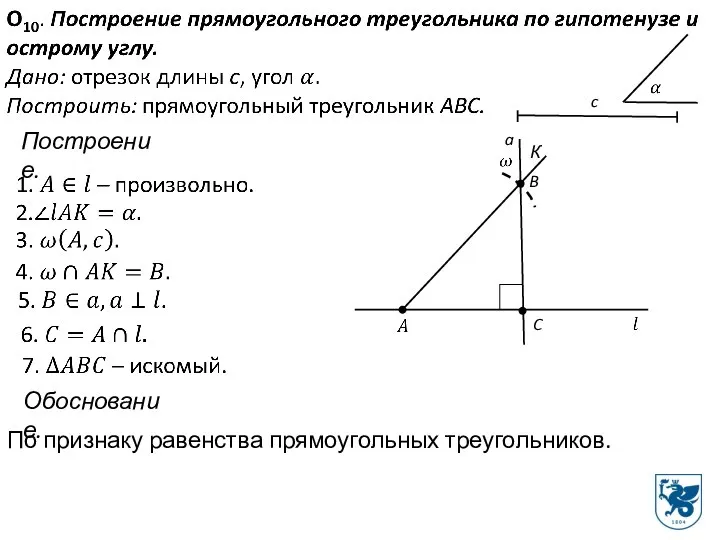
- 18. Построение. C К B a Обоснование. По признаку равенства прямоугольных треугольников.
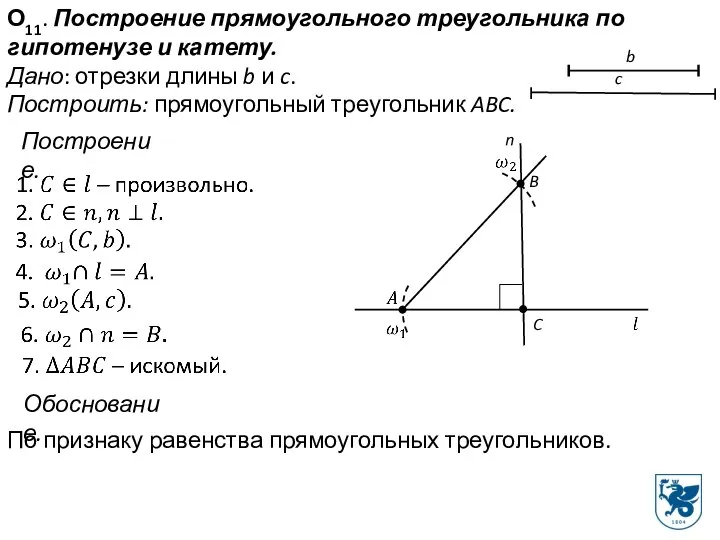
- 19. О11. Построение прямоугольного треугольника по гипотенузе и катету. Дано: отрезки длины b и c. Построить: прямоугольный
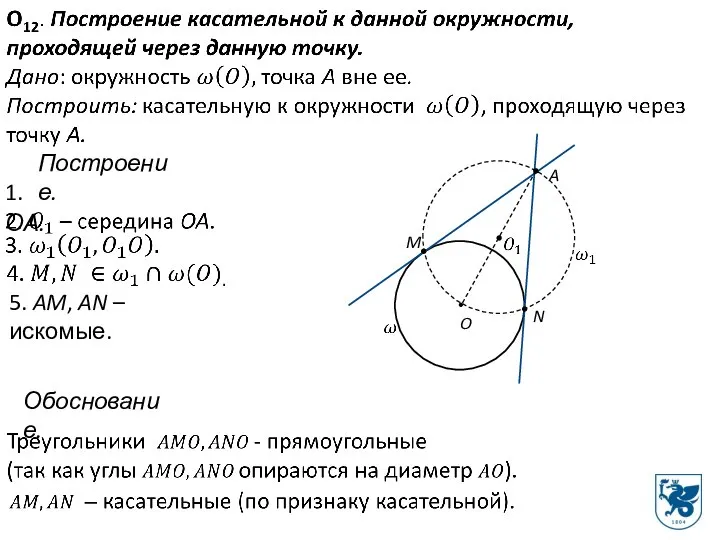
- 20. Построение. 1. ОА. 5. AM, AN – искомые. M N Обоснование.
- 21. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ НА ПОСТРОЕНИЕ Каждая фигура, удовлетворяющая условию задачи, называется решением этой задачи. Найти решение
- 22. При решении каждой сколь-нибудь сложной задачи возникает вопрос – как нужно рассуждать, чтобы найти способ построения
- 23. ПОСТРОЕНИЕ состоит в том, чтобы указать последовательность простейших и основных построений, которые надо выполнить для решения
- 25. Скачать презентацию












 Презентация на тему НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
Презентация на тему НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ  Алгебра в жизни человека
Алгебра в жизни человека Многогранники в нашей жизни
Многогранники в нашей жизни Построение призмы с вырезом
Построение призмы с вырезом Первая теорема сравнения
Первая теорема сравнения Тождественные преобразования алгебраических выражений (часть 1)
Тождественные преобразования алгебраических выражений (часть 1) Числовая окружность
Числовая окружность Исследование функций с помощью производных. Правила Лопиталя
Исследование функций с помощью производных. Правила Лопиталя Пределы. Раскрытие неопределенности. 2 часть
Пределы. Раскрытие неопределенности. 2 часть Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Логарифмы вокруг нас
Логарифмы вокруг нас В мире геометрии
В мире геометрии Штангенциркуль. Проведение измерений с помощью штангенциркуля
Штангенциркуль. Проведение измерений с помощью штангенциркуля Векторы
Векторы Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Вычитание вида 8 - ,9-
Вычитание вида 8 - ,9-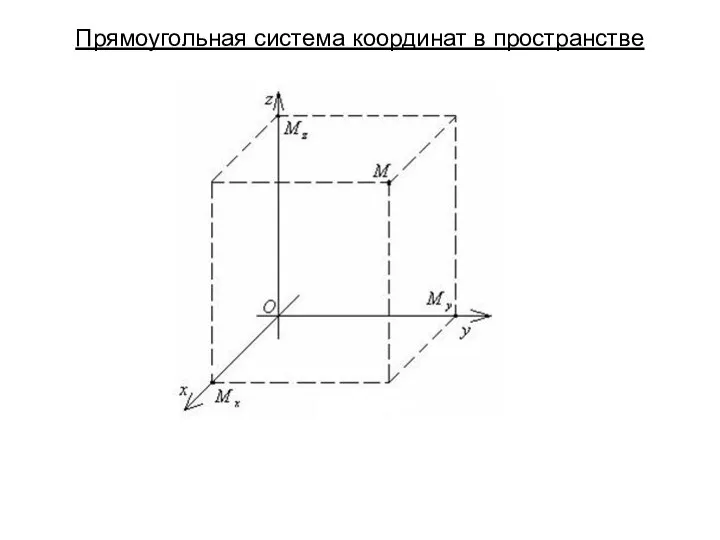 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Скрипт параллелограм
Скрипт параллелограм Двойные интегралы
Двойные интегралы Геометрия на каждом уроке
Геометрия на каждом уроке Преобразование графиков функции
Преобразование графиков функции Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Сумма углов треугольника
Сумма углов треугольника Повторение. Урок для 8 класса
Повторение. Урок для 8 класса Виды углов
Виды углов Классическое определение вероятности события
Классическое определение вероятности события Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Применение производной к исследованию функций
Применение производной к исследованию функций