Содержание
- 2. Пусть задан график функции y = f(x) Преобразование вида y = kf(x) Преобразование вида y =
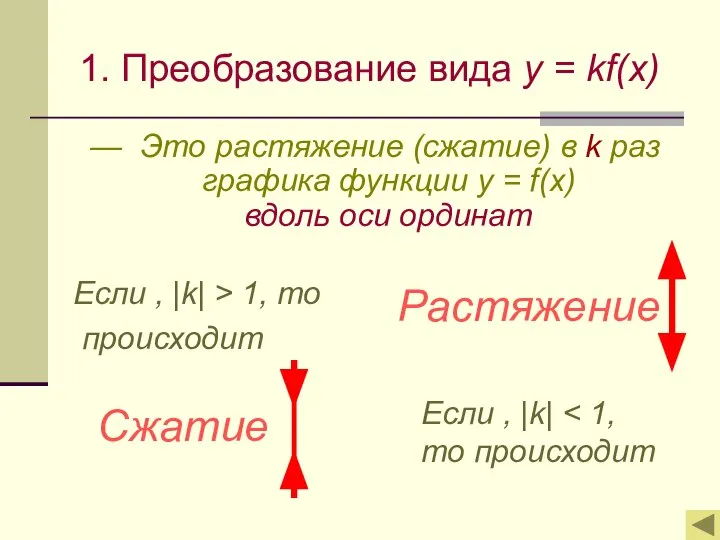
- 3. 1. Преобразование вида y = kf(x) — Это растяжение (сжатие) в k раз графика функции y
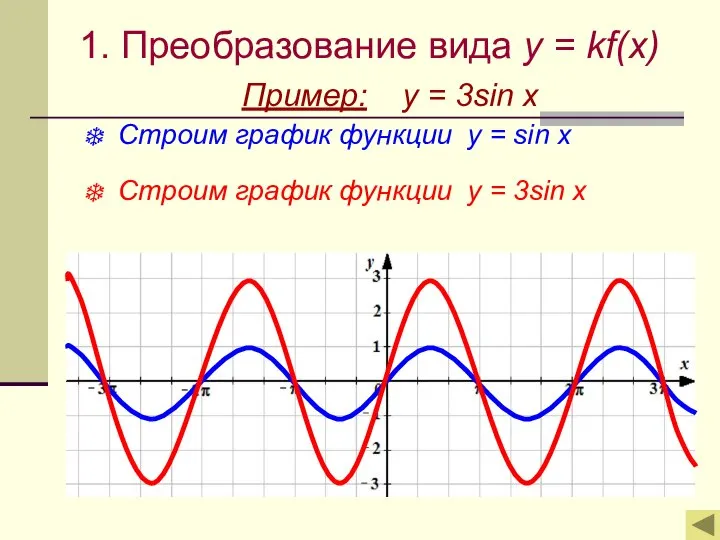
- 4. 1. Преобразование вида y = kf(x) Пример: y = 3sin x Строим график функции у =
- 5. 2. Преобразование вида y = f(x) + b — Это параллельный перенос графика функции y =
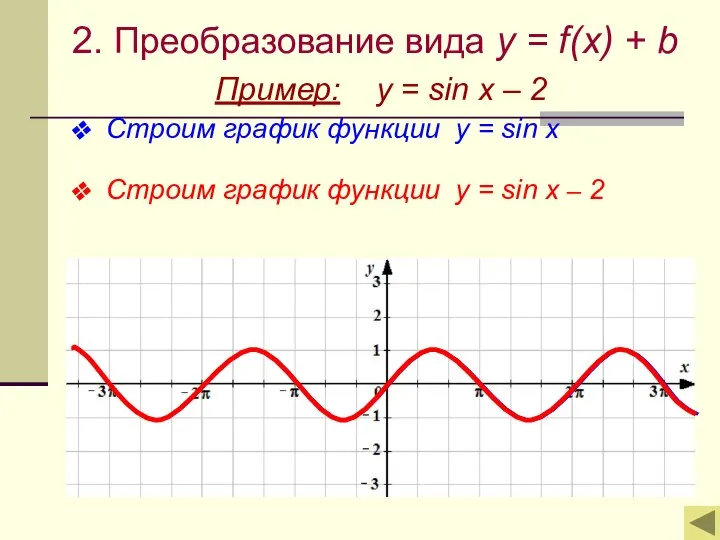
- 6. 2. Преобразование вида y = f(x) + b Пример: y = sin x – 2 Строим
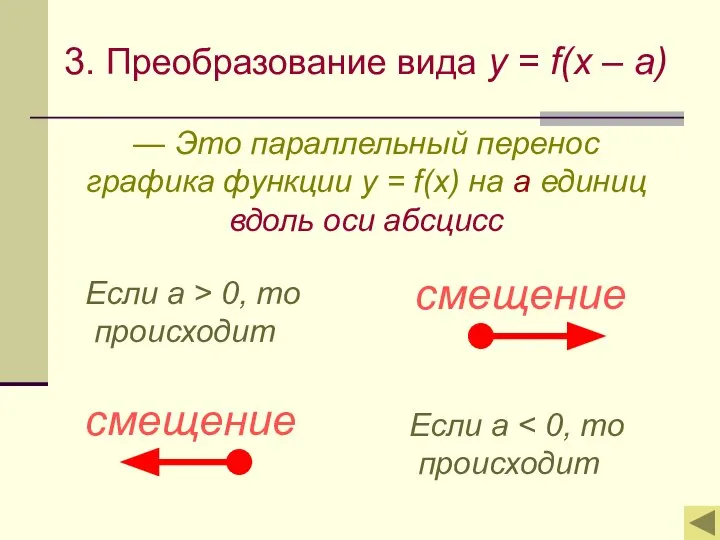
- 7. 3. Преобразование вида y = f(x – a) — Это параллельный перенос графика функции y =
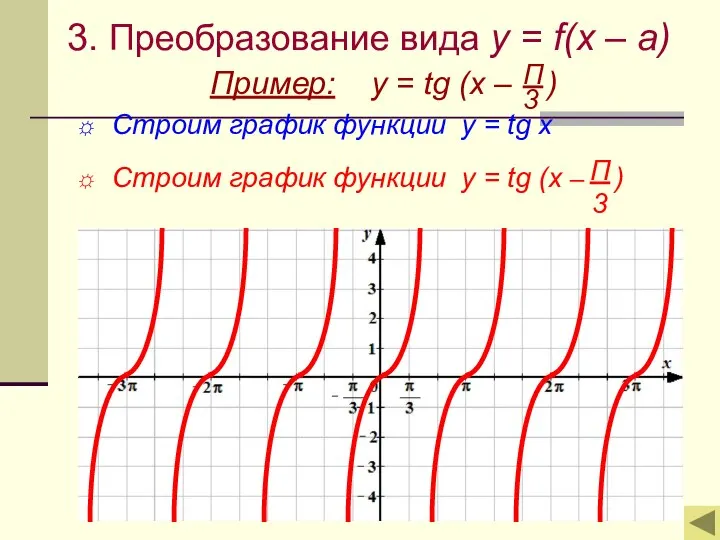
- 8. 3. Преобразование вида y = f(x – a) Пример: y = tg (x – ) Строим
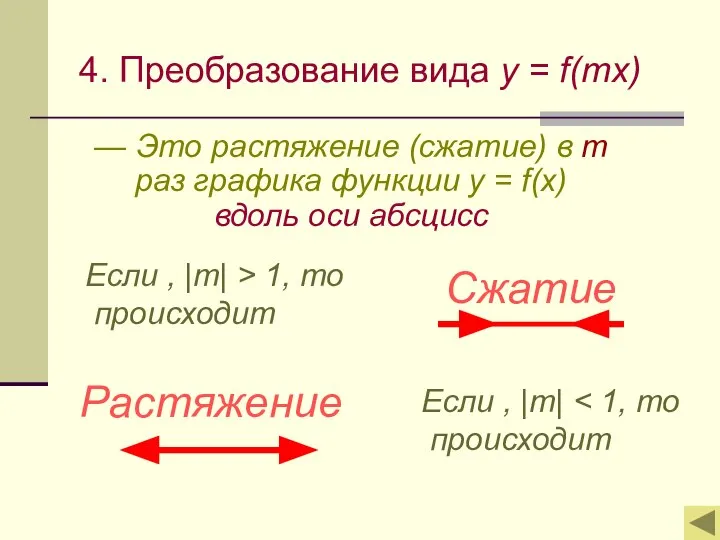
- 9. 4. Преобразование вида y = f(mx) — Это растяжение (сжатие) в m раз графика функции y
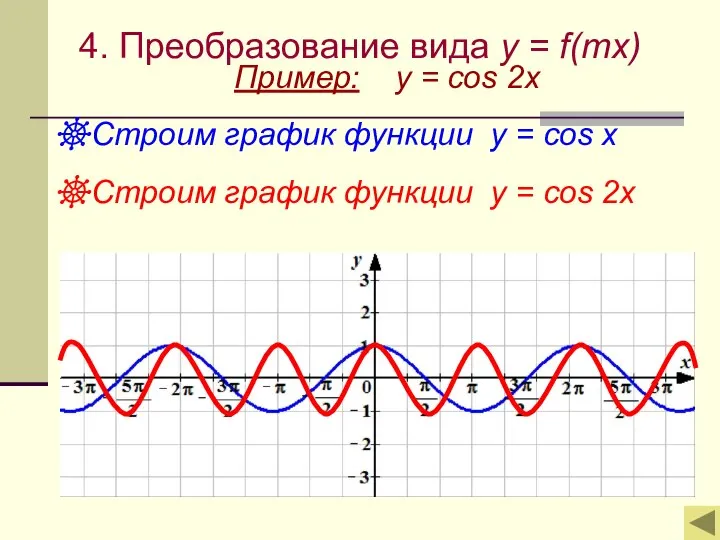
- 10. 4. Преобразование вида y = f(mx) Пример: y = cos 2x Строим график функции у =
- 11. 5. Преобразование вида y = |f(x)| — Это отображение нижней части графика функции y = f(x)
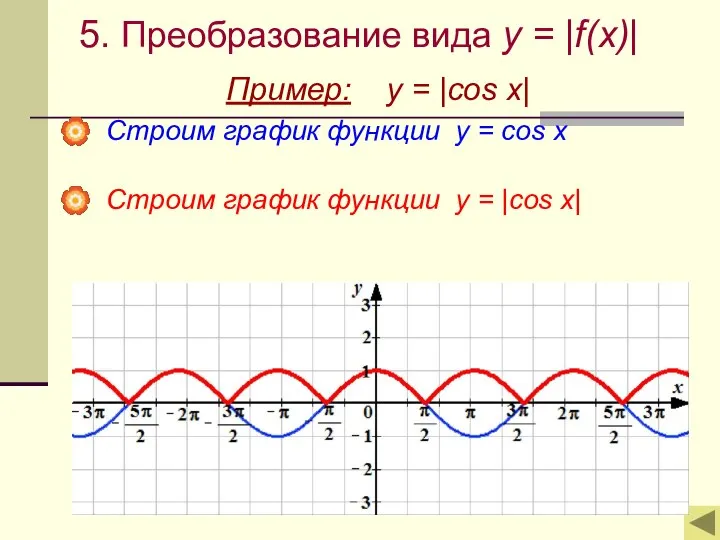
- 12. 5. Преобразование вида y = |f(x)| Пример: y = |cos x| Строим график функции у =
- 13. 6. Преобразование вида y = f (|x|) — Это отображение правой части графика функции y =
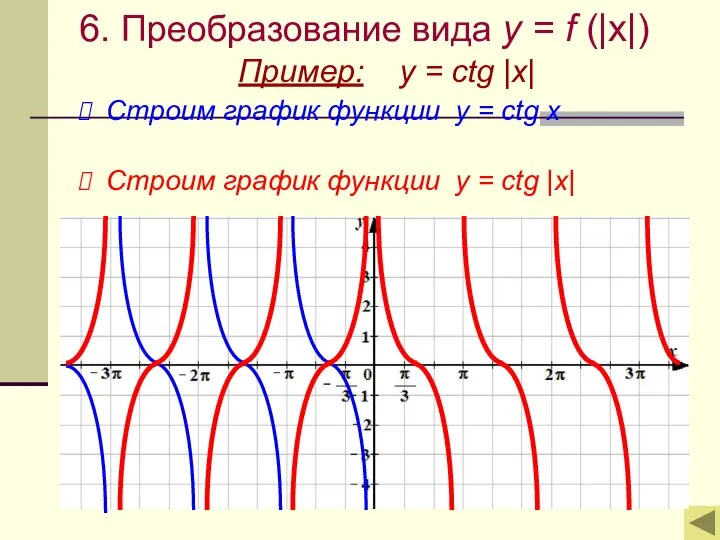
- 14. 6. Преобразование вида y = f (|x|) Пример: y = ctg |x| Строим график функции у
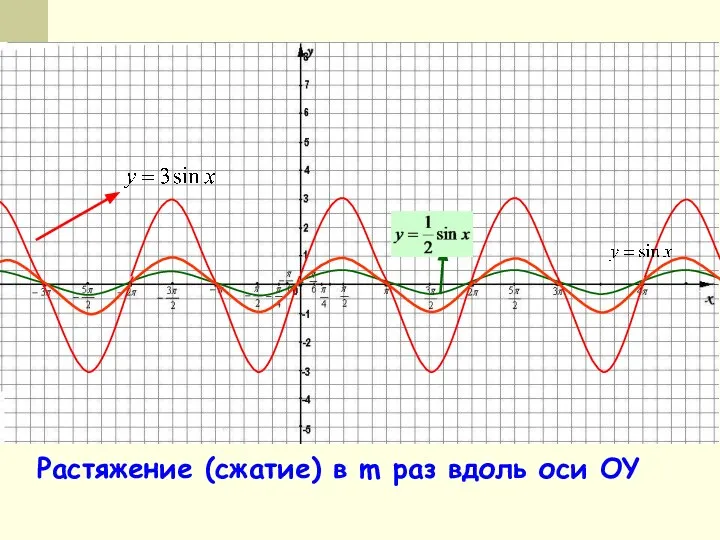
- 15. Растяжение (сжатие) в m раз вдоль оси OY
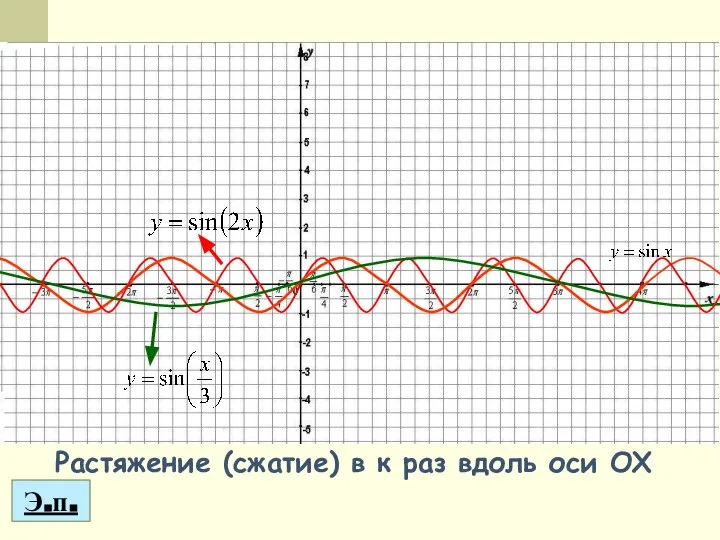
- 16. Растяжение (сжатие) в к раз вдоль оси OX Э.п.
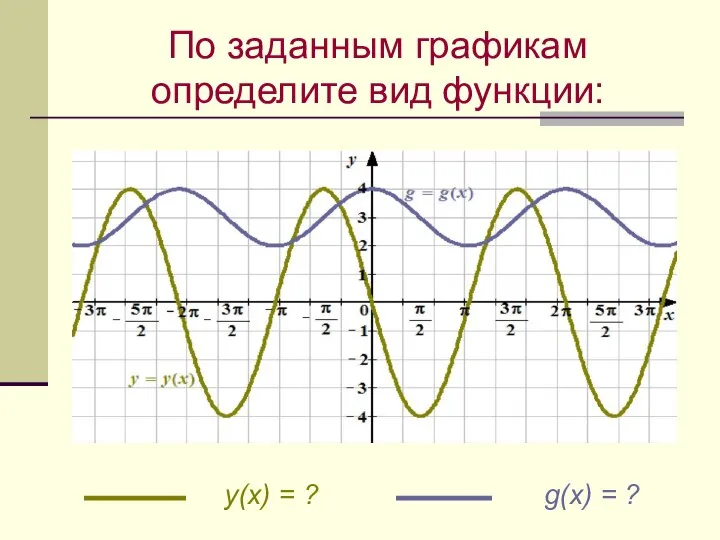
- 17. y(x) = ? g(x) = ? По заданным графикам определите вид функции:
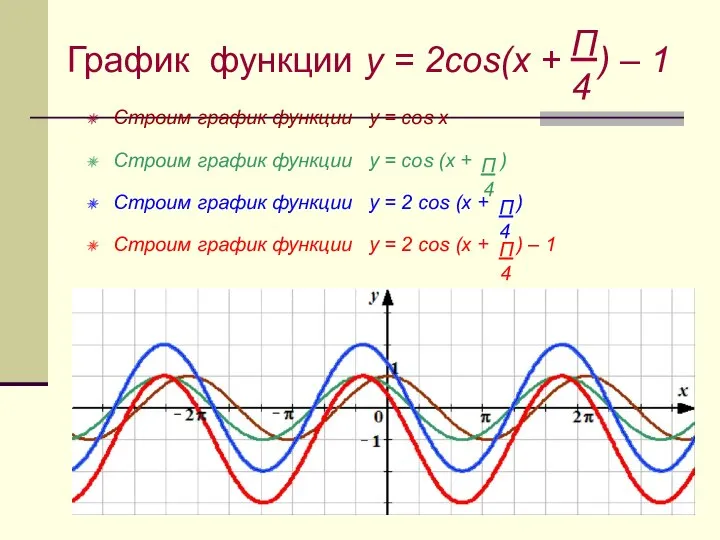
- 18. График функции y = 2cos(x + ) – 1 Строим график функции y = cos x
- 19. Постройте графики функций 1 3 2
- 21. Алгоритм построения функции y=|f(x)| 1) Строим график 2)Часть графика лежащую ниже оси Оx отображаем зеркально вверх,
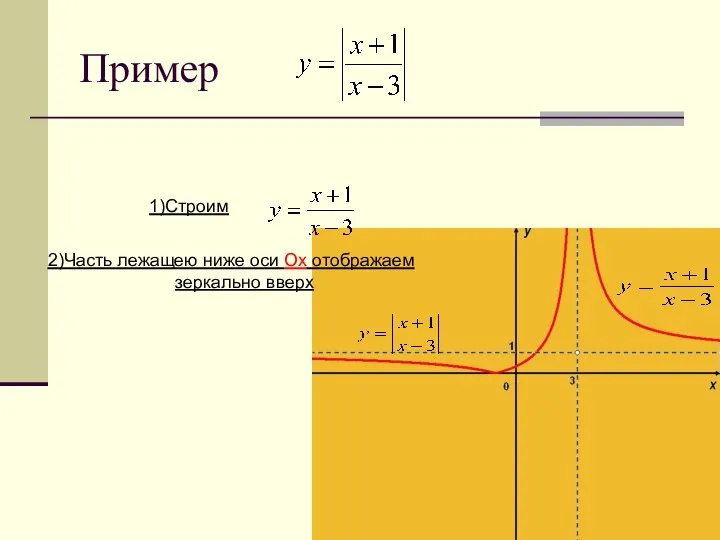
- 22. Пример 1)Строим 2)Часть лежащею ниже оси Оx отображаем зеркально вверх
- 23. Алгоритм построения функции y=f|x| Строим график функции y=f(x), где x ≥0 Эту часть графика отображаем симметрично
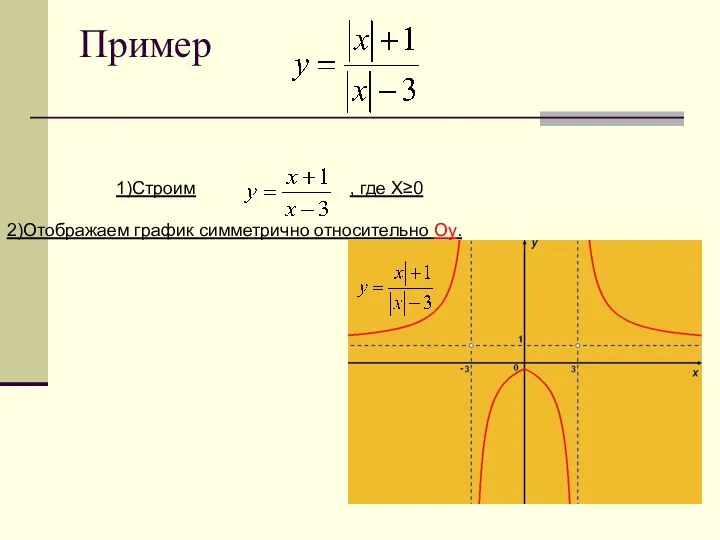
- 24. Пример 1)Строим 2)Отображаем график симметрично относительно Oy. , где X≥0
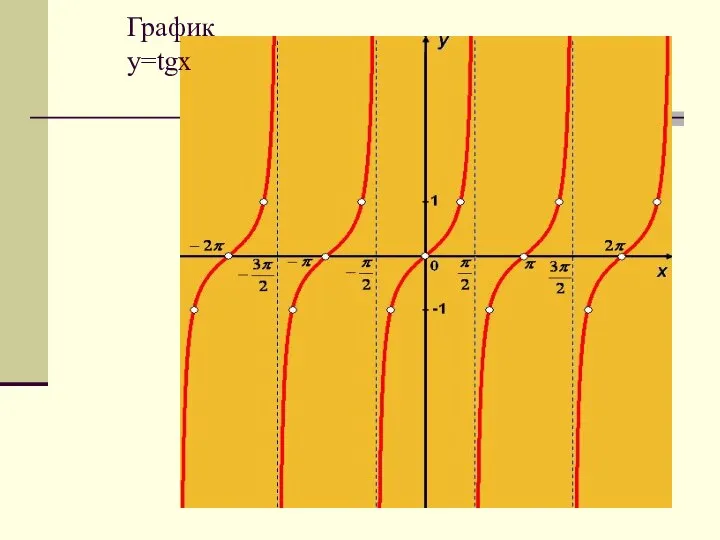
- 25. График y=tgx
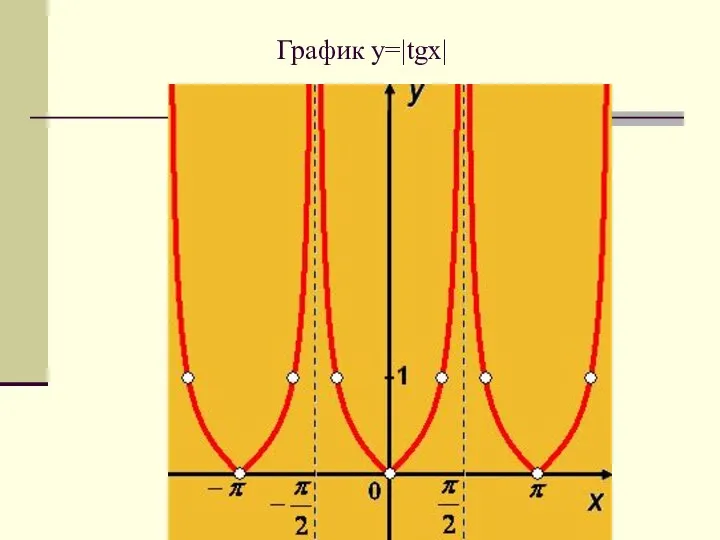
- 26. График y=|tgx|
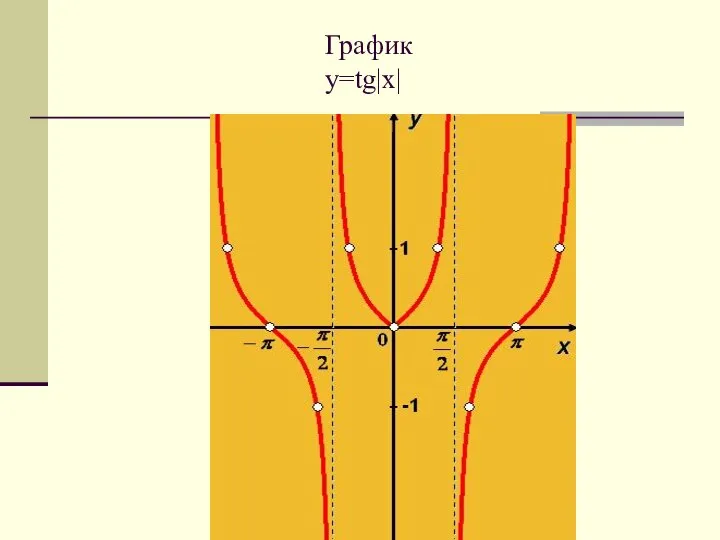
- 27. График y=tg|x|
- 28. Примеры построения графиков сложных функций Постройте график:
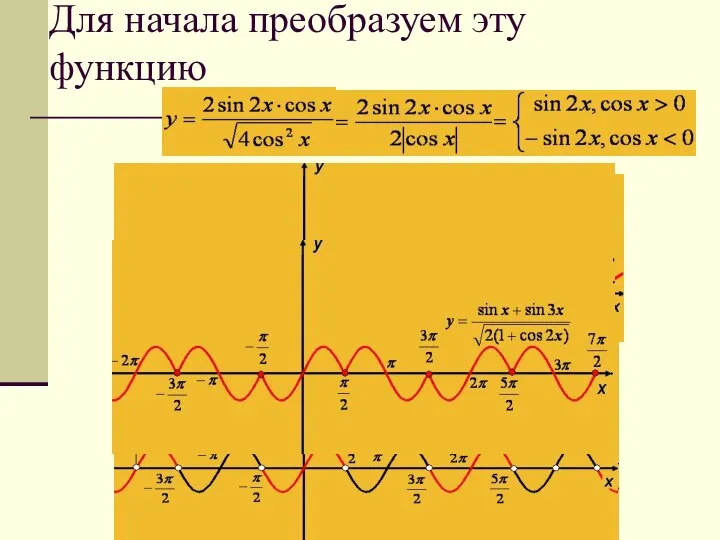
- 29. Для начала преобразуем эту функцию
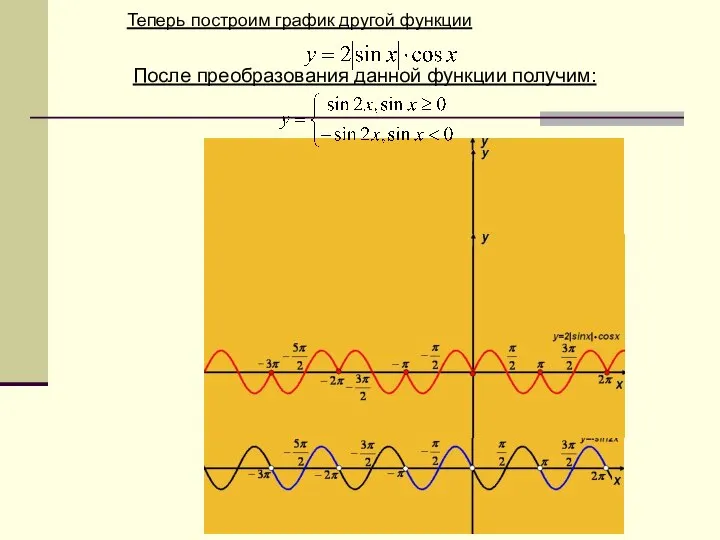
- 30. Теперь построим график другой функции После преобразования данной функции получим:
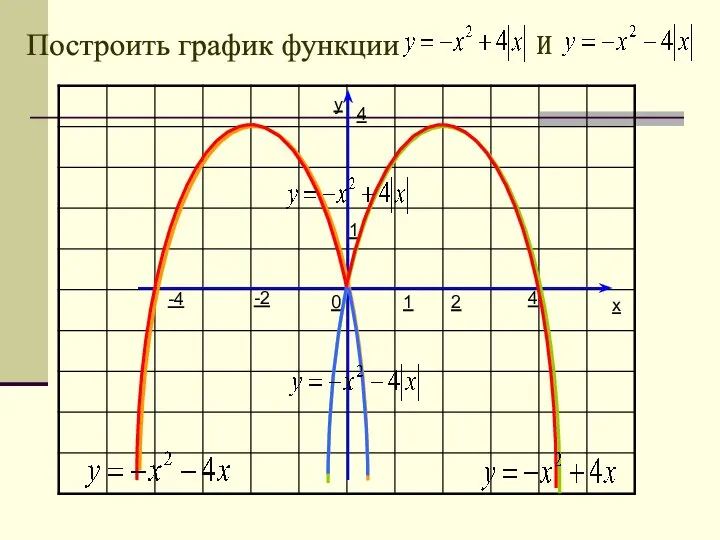
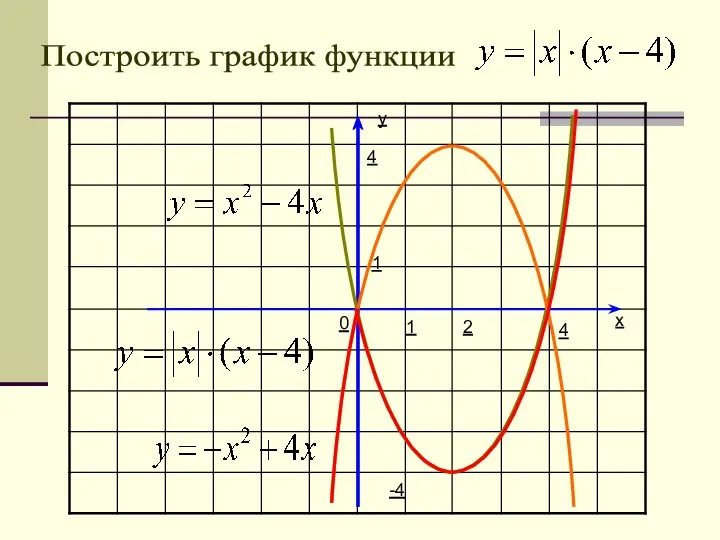
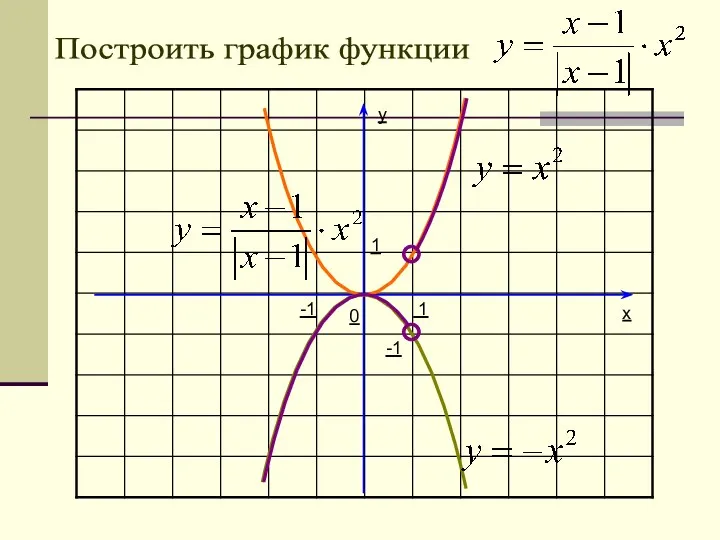
- 31. y x 1 1 0 Построить график функции 4 -4 4 2 -2 и
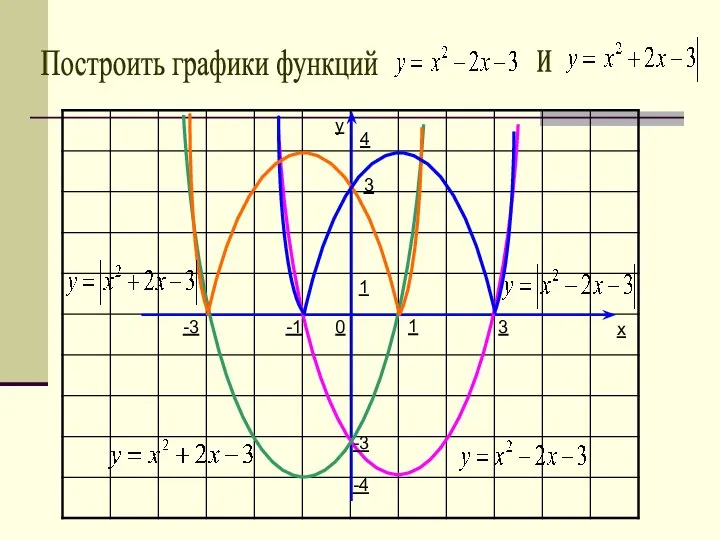
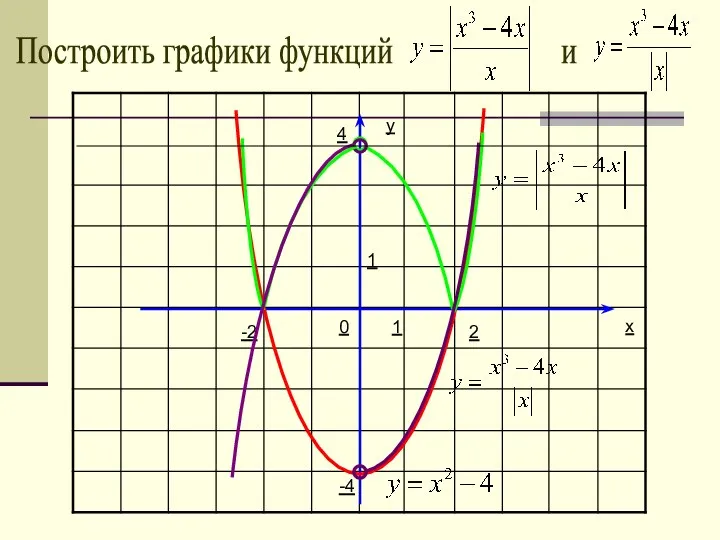
- 32. y x 1 1 0 Построить графики функций -4 3 -3 -1 4 -3 3 и
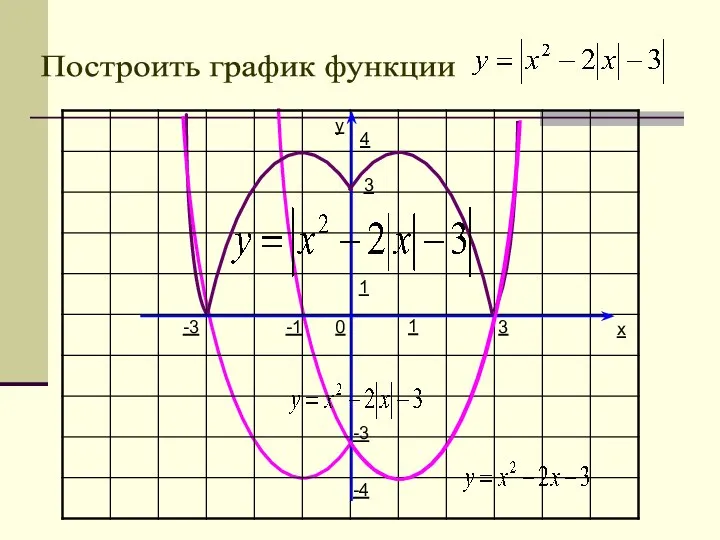
- 33. y x 1 1 0 Построить график функции -4 3 -3 -1 4 -3 3
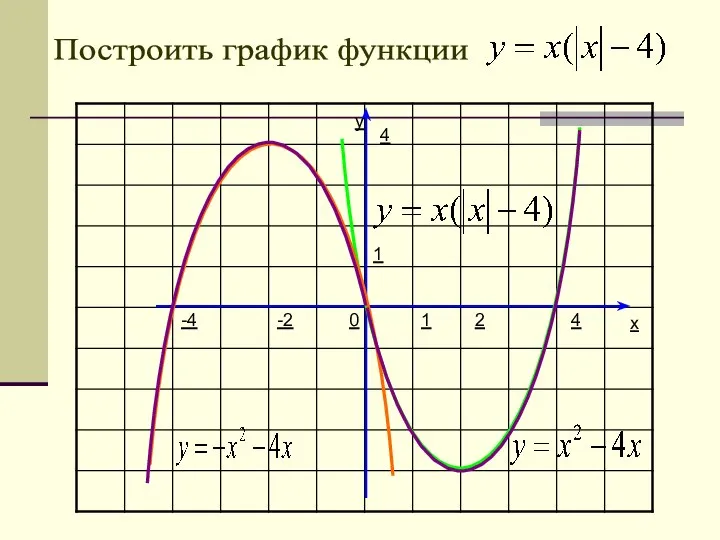
- 34. y x 1 1 0 Построить график функции 4 -4 4 -2 2
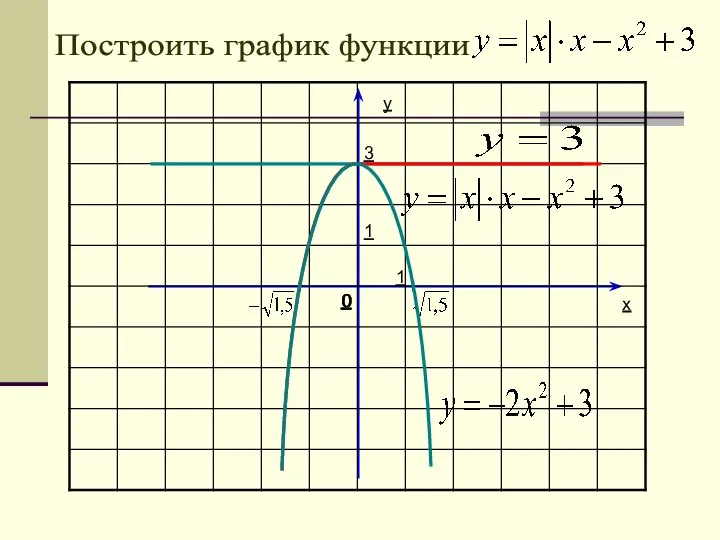
- 35. y 1 1 0 Построить график функции 4 -4 4 2 x
- 36. y x 0 0 0 0 Построить график функции 1 1 3
- 37. y x 1 1 0 Построить график функции -1 -2 -2
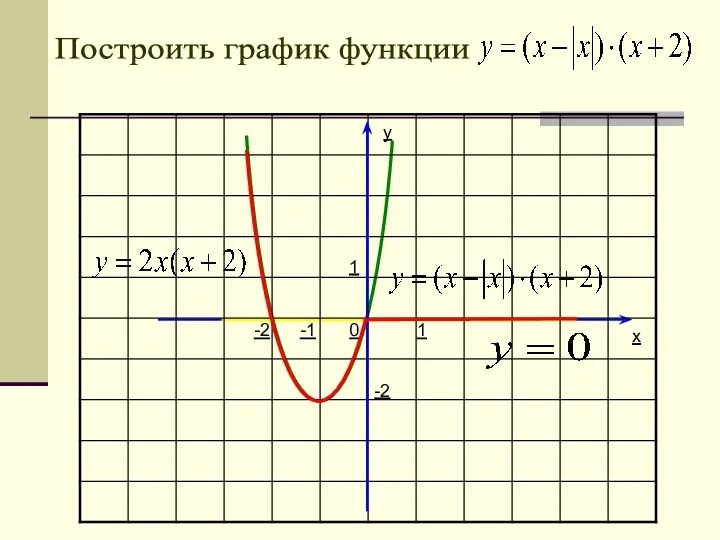
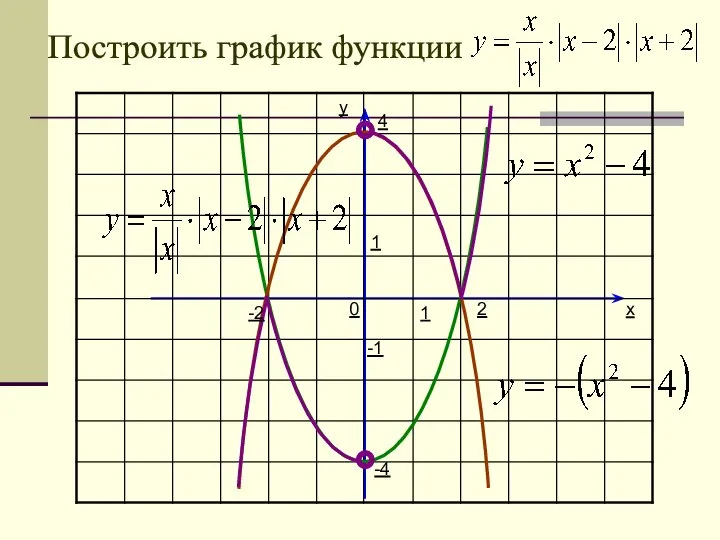
- 38. y x 1 1 2 -2 0 -4 4 Построить графики функций и
- 39. Построить график функции 1 1 x y 0 -1 -1
- 40. Построить график функции 0 1 1 -2 2 4 -4 -1 x y
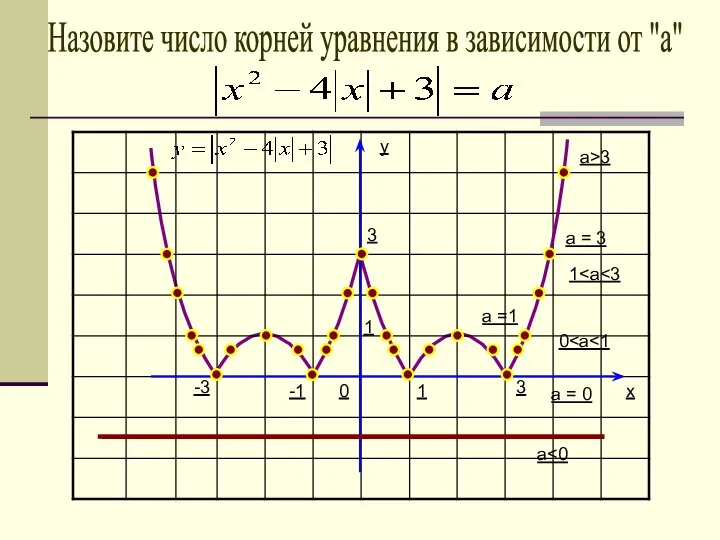
- 41. y x 1 1 0 Назовите число корней уравнения в зависимости от "a" 3 a a
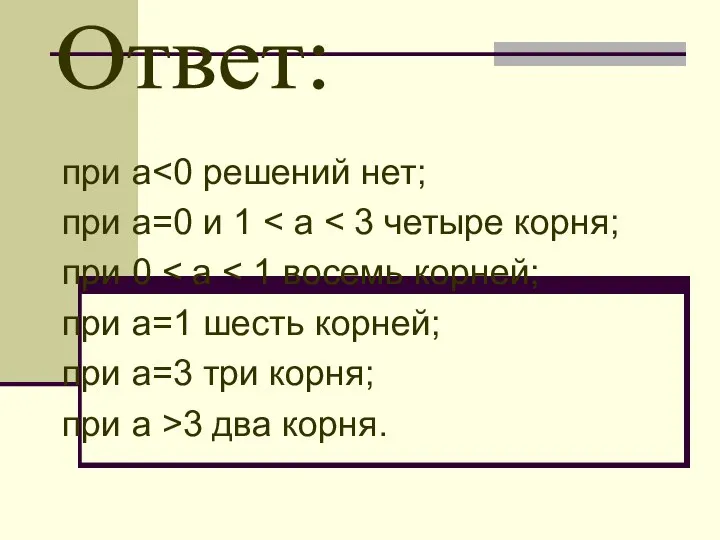
- 42. Ответ: при а при а=0 и 1 при 0 при а=1 шесть корней; при а=3 три
- 44. Скачать презентацию









 Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Исследование функции с помощью производной и построение графика функции
Исследование функции с помощью производной и построение графика функции Акула. Примеры
Акула. Примеры Линейная функция
Линейная функция Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Презентация на тему Наибольший общий делитель, наименьшее общее кратное
Презентация на тему Наибольший общий делитель, наименьшее общее кратное  Построение графика функции
Построение графика функции Математическая раскраска
Математическая раскраска Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Математические приемы быстрого счета (лайфхаки)
Математические приемы быстрого счета (лайфхаки) Цикломатика графов
Цикломатика графов Профильная математика № 17
Профильная математика № 17 Производная степенной функции. Производная и её геометрический смысл
Производная степенной функции. Производная и её геометрический смысл Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Эволюционные этапы развития логистики
Эволюционные этапы развития логистики Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)
Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)  Аксиомы стереометрии
Аксиомы стереометрии Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Определитель второго порядка
Определитель второго порядка Пропорциональность величин
Пропорциональность величин Построение графика функции
Построение графика функции Допуск прямолинейности
Допуск прямолинейности Множення і ділення десяткових дробів. 5 клас
Множення і ділення десяткових дробів. 5 клас Что такое проекция вектора
Что такое проекция вектора У гостях у Цвіріньчика
У гостях у Цвіріньчика Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1)