- Главная
- Математика
- Расчет изгиба балки методом конечно-разностных элементов

Содержание
Слайд 8Решение задачи
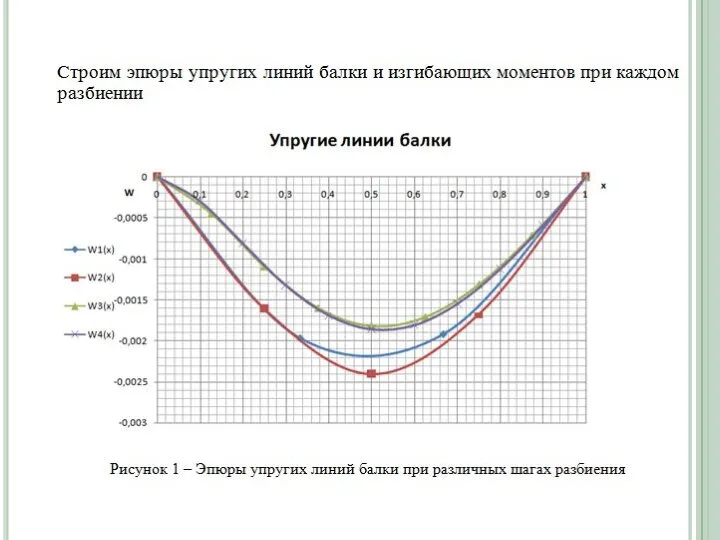
Решение задачи
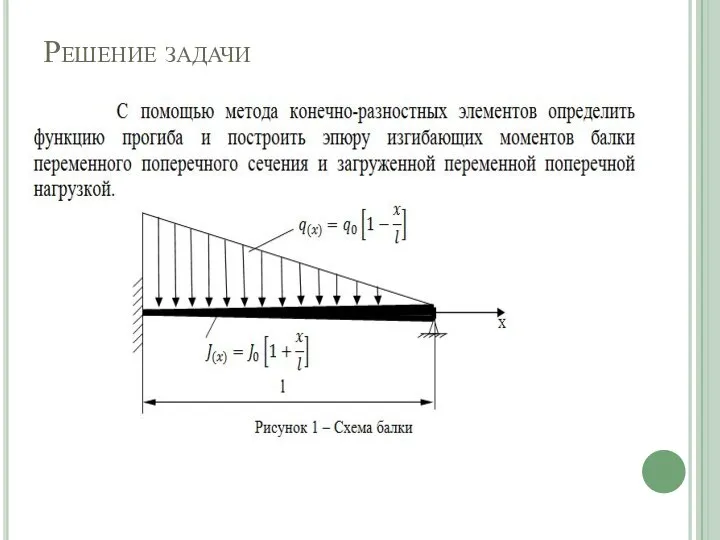
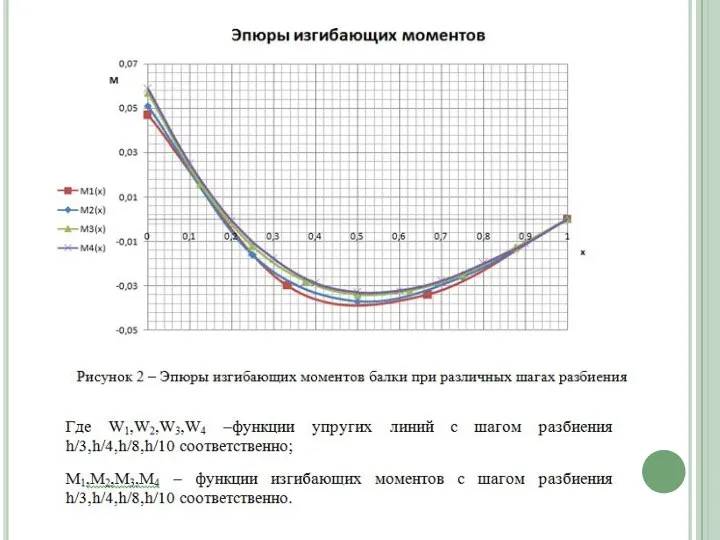
Слайд 25Анализируя полученные зависимости можно сделать вывод: чем меньше шаг разбиения (т.е. на
Анализируя полученные зависимости можно сделать вывод: чем меньше шаг разбиения (т.е. на

больше участков разбиваем наш предмет),тем точнее решение. Но следует заметить, что при шаге h/8 и h/10 разница минимальна, т.е. если мы возьмем h/11,h/12 и т.д. разница будет не существенна. Таким образом можно решить задачу с шагом h/10(что дает нам наиболее точное решение) и округляя в безопасную сторону (т.е. брать с коэффициентом запаса) анализировать ее работу при данном виде нагружении.
- Предыдущая
Биотические факторы
















 Деление обыкновенных дробей
Деление обыкновенных дробей Квадратный корень (алгебраический подход)
Квадратный корень (алгебраический подход) Презентация на тему Цилиндр (11 класс)
Презентация на тему Цилиндр (11 класс)  Презентация на тему Устный счет до десяти
Презентация на тему Устный счет до десяти  Численные методы решения СЛАУ (часть 2)
Численные методы решения СЛАУ (часть 2) Применение комплексных чисел на практике
Применение комплексных чисел на практике Признаки равенства треугольников
Признаки равенства треугольников Формулы сокращенного умножения
Формулы сокращенного умножения Теорема Пифагора
Теорема Пифагора Лекция. Ряды
Лекция. Ряды Великие математики
Великие математики РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания
РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания Формирование функциональной грамотности школьников на уроках математики через решение нестандартных задач
Формирование функциональной грамотности школьников на уроках математики через решение нестандартных задач Действия с алгебраическими дробями
Действия с алгебраическими дробями Решение уравнений. Простые уравнения
Решение уравнений. Простые уравнения Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Презентация на тему ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Презентация на тему ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА  Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7 Односторонние пределы
Односторонние пределы Нахождение sin и tg
Нахождение sin и tg Презентация на тему Натуральные числа
Презентация на тему Натуральные числа  Формулы двойного аргумента
Формулы двойного аргумента Презентация на тему Четырехугольники вокруг нас
Презентация на тему Четырехугольники вокруг нас  Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Три кота. Прибавление и вычитание числа 2
Три кота. Прибавление и вычитание числа 2 Нейронные сети и их применение
Нейронные сети и их применение Презентация на тему Сложение и вычитание дробей с разными знаменателями
Презентация на тему Сложение и вычитание дробей с разными знаменателями  Четырехугольники
Четырехугольники