Презентация на тему Призма и ее свойства

Содержание
Историческая справка
Призма и ее свойства
Решение задач
Задачи для самостоятельной работы
Литература

Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию – как границу поверхности, концы же линии – как точки.
Историческая справка
Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию – как границу поверхности, концы же линии – как точки.

Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д.
Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности.
Историческая справка

В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения.
Историческая справка

Евклид употребляет термин «плоскость» как в широком смысле (Рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина «прямая» ( в широком смысле - бесконечная прямая и в узком – отрезок).
Историческая справка

В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Историческая справка

В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Историческая справка

Термин “призма” греческого происхождения и буквально означает “отпиленное”
ПризмА

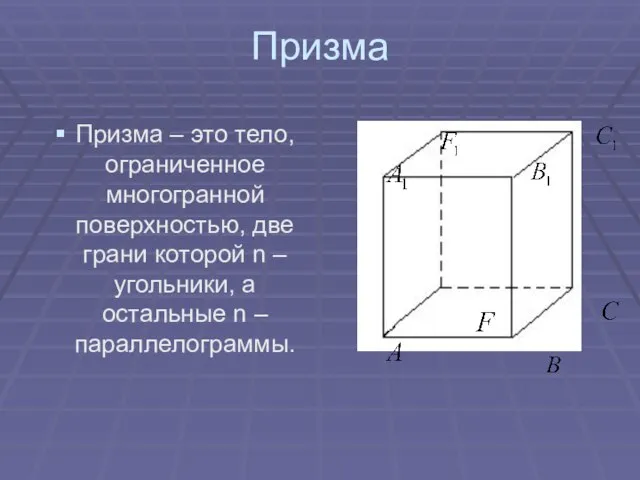
Призма
Призма – это тело, ограниченное многогранной поверхностью, две грани которой n – угольники, а остальные n – параллелограммы.

β
Рассмотрим два равных многоугольника
и , расположенных в параллельных плоскостях и так, что отрезки , , ..., , соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
ПризмА
β
α
1
1
В
А

Каждый из n четырехугольников
является параллелограммов, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике стороны и параллельны по условию, а стороны и - по свойству параллельных плоскостей, пересеченных третьей
плоскостью (рис. 2).
ПризмА

( рис. 3)
Многоугольники и называются основаниями, а параллелограммы – боковыми гранями. Отрезки , называются боковыми ребрами призмы.
Призму с основаниями и
n - угольной призмой.
ПризмА
( рис. 3)

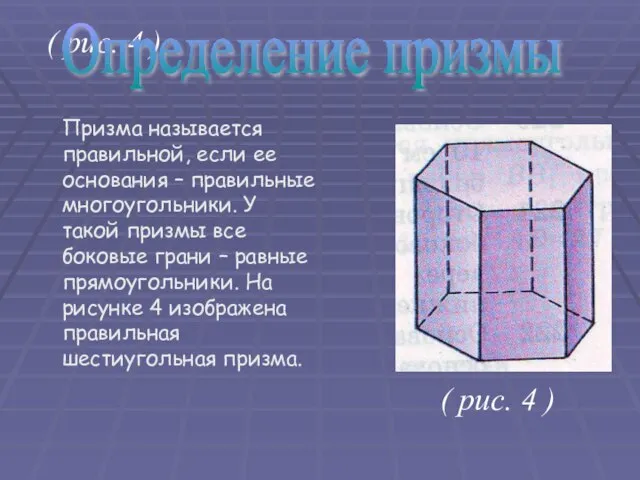
( рис. 4 )
Призма называется правильной, если ее основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники. На рисунке 4 изображена правильная шестиугольная призма.
Определение призмы
( рис. 4 )

Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные,
четырехугольные, пятиугольные и т.д.,
в зависимости от числа вершин основания.
ПризмА

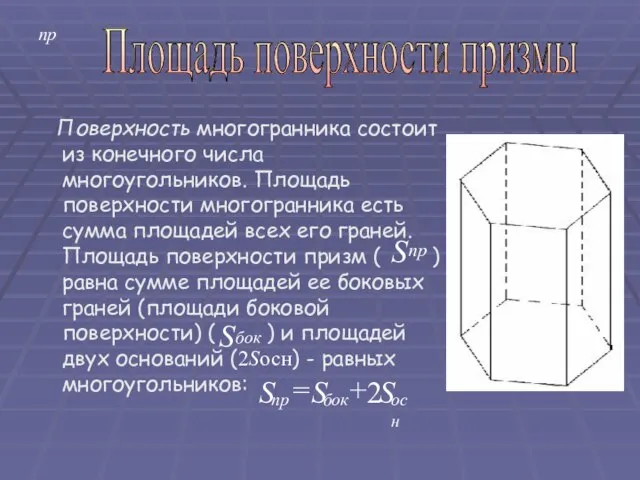
пр
Поверхность многогранника состоит из конечного числа многоугольников. Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм ( ) равна сумме площадей ее боковых граней (площади боковой поверхности) ( ) и площадей двух оснований (2Sосн) - равных многоугольников:
Площадь поверхности призмы

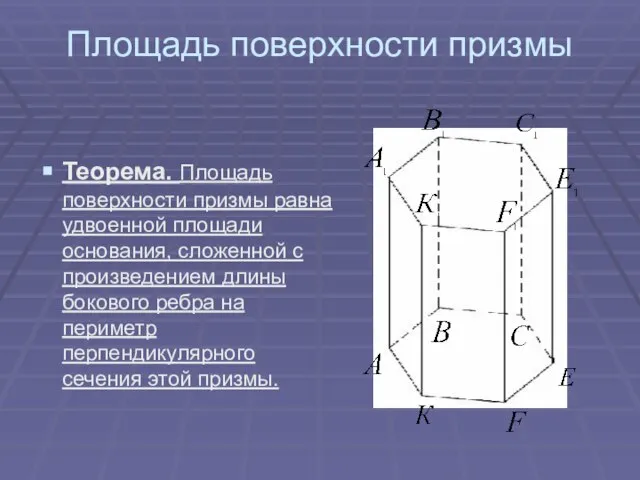
Площадь поверхности призмы
Теорема. Площадь поверхности призмы равна удвоенной площади основания, сложенной с произведением длины бокового ребра на периметр перпендикулярного сечения этой призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны призмы, а высоты равны высоте h призмы.
Площадь боковой поверхности призмы равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. его периметр Р.
Итак, Sбок=Рh.
Теорема доказана.
Доказательство

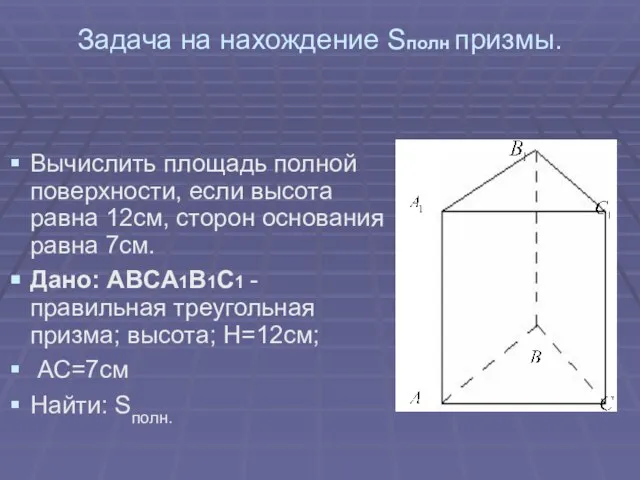
Задача на нахождение Sполн призмы.
Вычислить площадь полной поверхности, если высота равна 12см, сторон основания равна 7см.
Дано: ABCA1B1C1 - правильная треугольная призма; высота; Н=12см;
АС=7см
Найти: Sполн.

Решение:
Ответ:

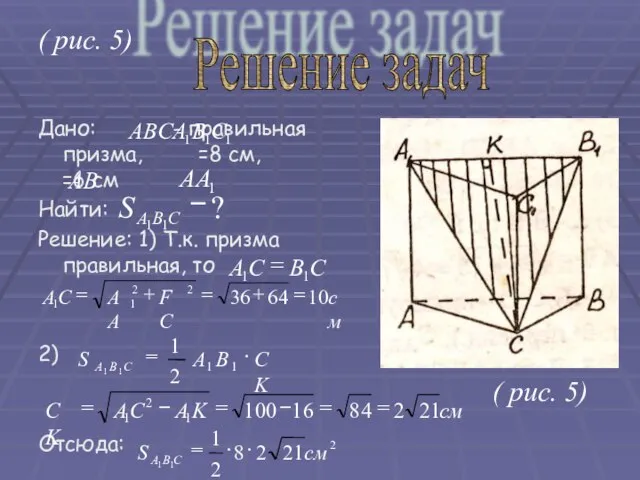
( рис. 5)
Дано: - правильная призма, =8 см, =6 см
Найти:
Решение: 1) Т.к. призма правильная, то
2)
Отсюда:
Решение задач
( рис. 5)
АВ

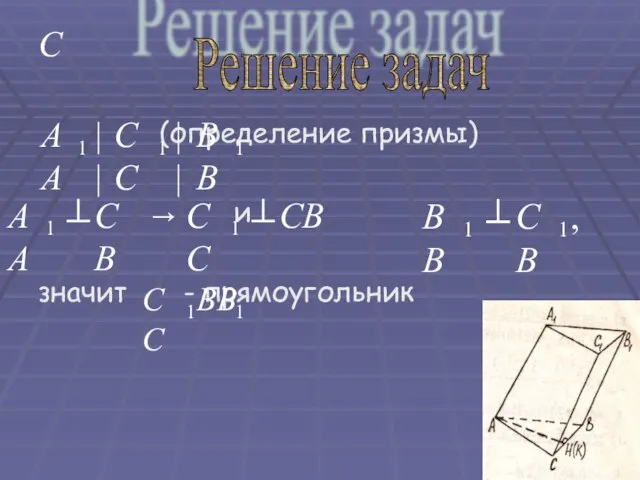
Дано:
- правильный
Доказать: а) б)
прямоугольник
Доказательство:
1) Т.к. , то АН -
биссектриса
- равносторонний, значит по свойству биссектрисы и , значит
( рис. 6)
Решение задач
( рис. 6)

(определение призмы)
и
значит - прямоугольник
C
Решение задач

Докажите, что:
а) у прямой призмы все боковые грани – прямоугольники; б) у правильной призмы все боковые грани – равные прямоугольники.
Сторона правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдете площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Задачи для самостоятельной работы

Основаниями прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двухгранные углы при боковых ребрах призмы.
Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол 30`. Найдите угол между диагональю и плоскостью основания.
Задачи для самостоятельной работы