Содержание
- 2. План Мода та її обчислення. Медіана та її обчислення. Середнє арифметичне: обчислення та властивості. Інтерпретація мір
- 3. Первинні методи кількісної обробки даних До основних методів первинної статистичної обробки відносяться обчислення: мір центральної тенденції
- 4. 1) яке значення найбільш характерне для вибірки? 2) чи великий розкид даних щодо цього характерного значення,
- 5. Міри центральної тенденції
- 6. Мода – це значення у множині спостережень, яке зустрічається найчастіше Аналiзується сукупнiсть статистичних даних X1, X2,
- 7. При визначенні моди необхідно дотримуватись таких вимог: 1. Якщо в даних всі значення зустрічаються однаково часто,
- 8. При визначенні моди необхідно дотримуватись таких вимог:
- 9. При визначенні моди необхідно дотримуватись таких вимог: 3. Якщо два несусідні значення мають однакову частоту, то
- 10. Приклад Студенти академiчної групи отримали настпуні оцiнки на екзаменi. Оцiнку “2” на екзаменi у групi отримали
- 11. Приклад Припустимо, маємо тест з 40 питань для визначення типу темпераменту у людини за встановленою методикою.
- 12. Приклад Розглянемо результати соцiологiчного дослiдження, здiйсненого з метою встановлення середньої кiлькостi дiтей у сiм’ї. Загалом було
- 13. Медіана значення, яке перебуває на середині упорядкованої послідовності емпіричних даних. це значення, яке ділить упорядковану множину
- 14. При визначенні медіани необхідно дотримуватись таких вимог: 1) якщо кількість спостережень у вибірці непарне, то медіана
- 16. При визначенні медіани необхідно дотримуватись таких вимог:
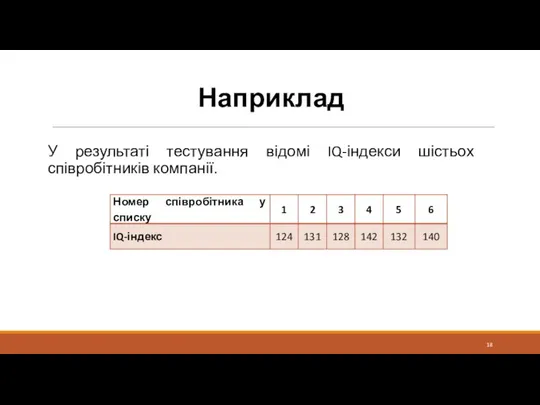
- 18. Наприклад У результаті тестування відомі IQ-індекси шістьох співробітників компанії.
- 20. Середнє арифметичне
- 21. Наприклад
- 22. Приклад Обчислити моду, медіану і середнє значення вибірки, поданої у вигляді статистичного розподілу: 1) модою є
- 23. Розв’язання 2) для визначення медіани спочатку визначимо, скільки значень містить вибірка: n=15 – непарне. Тоді медіаною
- 24. Розв’язання 3) для визначення середнього значення потрібно кожне значення хі помножити на його частоту nі, добуток
- 25. Особливості мір центральної тенденції мода вибірки обчислюється просто, її можна визначити «на око». Для дуже великих
- 26. Особливості мір центральної тенденції Медіана обчислюється в тому випадку, коли у серії є «нетипові» дані, що
- 27. Поради, щодо визначення мір центральної тенденції 1. Моду та медіану обчислити найпростіше. 2. В малих групах
- 28. Поради, щодо визначення мір центральної тенденції 4. На величину середнього арифметичного впливають значення кожного елементу ряду.
- 29. Поради, щодо визначення мір центральної тенденції
- 31. Скачать презентацию



























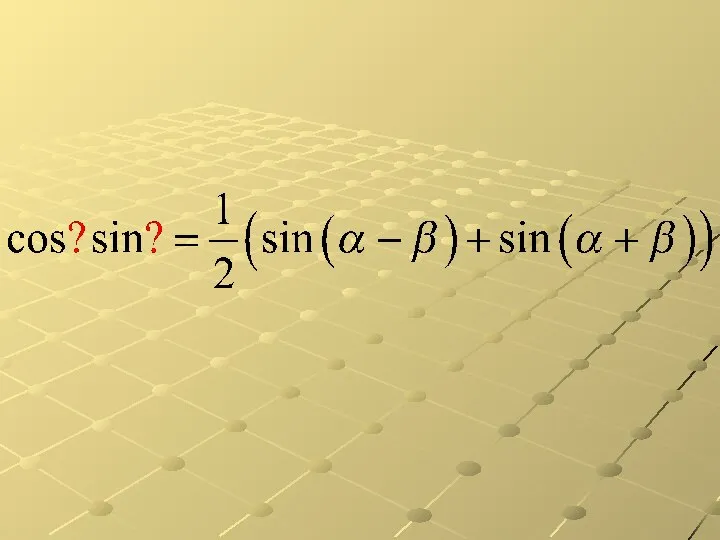 Тригонометрические формулы. Диктант
Тригонометрические формулы. Диктант Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Чертежи и развертки простых геометрических тел
Чертежи и развертки простых геометрических тел Презентация на тему Луч и угол (7 класс)
Презентация на тему Луч и угол (7 класс)  Графики степенных функций
Графики степенных функций Коварные диаграммы
Коварные диаграммы Площадь треугольника
Площадь треугольника Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Понятие о проценте
Понятие о проценте Задачи на проценты
Задачи на проценты Многоугольники в нашей жизни
Многоугольники в нашей жизни Последовательность трехзначных чисел
Последовательность трехзначных чисел Равнобедренный треугольник
Равнобедренный треугольник Симметрия вокруг нас
Симметрия вокруг нас Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Создание геометрических тел
Создание геометрических тел Построение сечений тетраэдра
Построение сечений тетраэдра Код Церетели
Код Церетели Презентация на тему Действия с натуральными числами
Презентация на тему Действия с натуральными числами  Сравнение чисел
Сравнение чисел Числовой коэффициент
Числовой коэффициент Тренажер Вычисление производных
Тренажер Вычисление производных Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Какие бывают графы
Какие бывают графы Комбинаторные задачи
Комбинаторные задачи Деление дробей. 6 класс
Деление дробей. 6 класс