Применение производной к построению графиков функций

Приведём общую схему исследования свойств функции с помощью
её производной.
1.
Сегодня на уроке
Будем строить график функции, используя результаты исследования.
2.

А
Б
В
Г

А
Б
В
Г

А
Б
В
Г

А
Б
В
Г

А
Б
В
Г

А
Б
В
Г

Вспомним

Вспомним

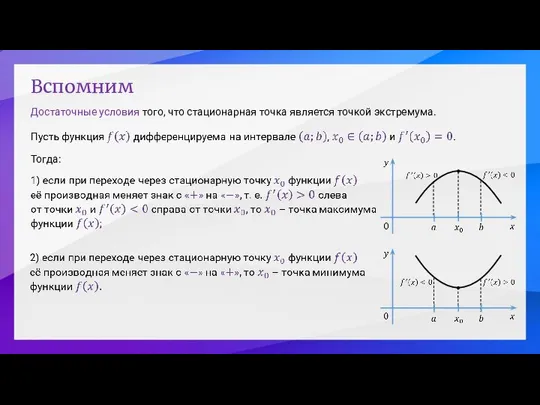
Вспомним
Достаточные условия того, что стационарная точка является точкой экстремума.
Тогда:

Вспомним
– стационарные точки данной функции.
Значение функции в точке максимума:
Значение функции в точке минимума:

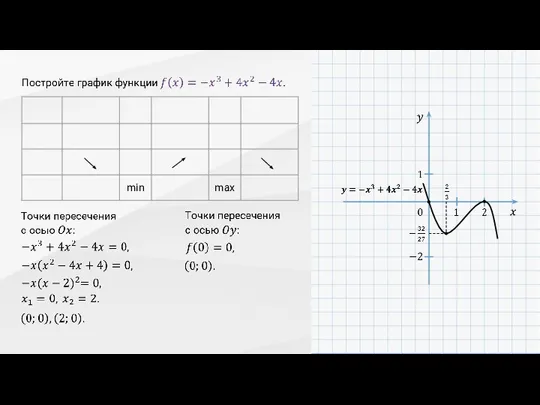
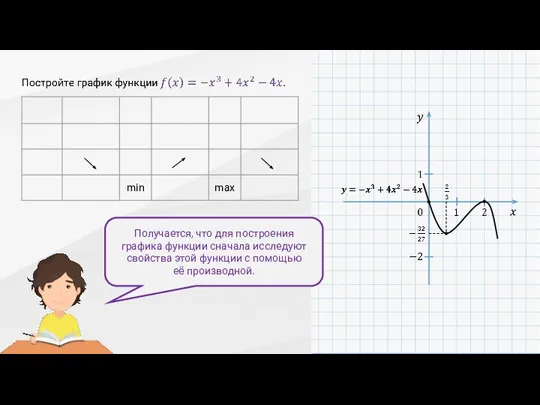
Получается, что для построения графика функции сначала исследуют свойства этой функции с помощью
её производной.

Схема исследования свойств функции
с помощью её производной
При исследовании свойств функции надо найти:
1) область определения;
2) производную;
3) стационарные точки;
4) промежутки возрастания и убывания;
5) точки экстремума и значения функции в этих точках.
Для более точного построения графика обычно находят точки пересечения
с осями координат.
Также можно найти координаты ещё нескольких точек графика.

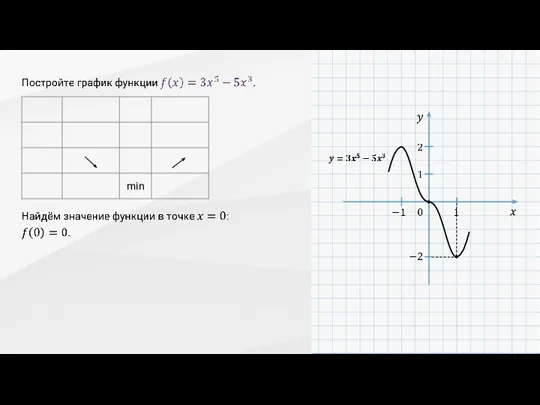
Данная функция нечётная,

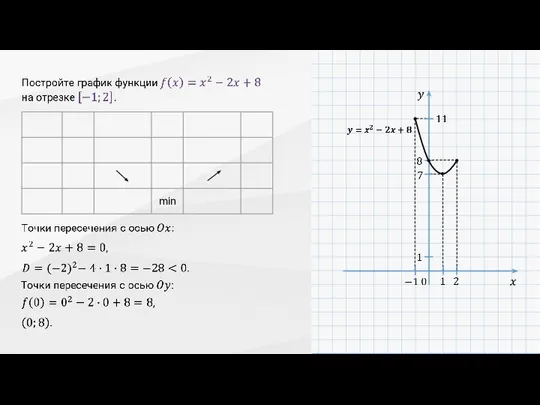
Получается, что график функции
не пересекает ось абсцисс.