Распределенные системы. Математическое представление распределенной системы

Лекция 2
Математическое представление распределенной системы
Сосредоточенные и распределенные системы
Распределенные задачи и алгоритмы
Надежность и безопасность распределенных систем

Математическое представление распределенной системы
Под системой понимается множество элементов и связей между ними.
Обозначим V – множество элементов системы. Тогда бинарное отношение R2 ⊆ V × V задает наличие попарных связей между элементами. Если для некоторых элементов x∈V и y∈V пара (x, y)∈ R2, то в системе существует связь от x к y. Если (x, y)∉ R2 , то такой связи нет.
Порядок элементов в паре важен, так как связи могут быть направленными, несимметричными.

В системе могут быть не только попарные связи, но и связи троек элементов. Такие связи описываются тернарными отношениями R3 ⊆ V × V × V = V3. Например, связь «ребенок и его родители» – связь трех элементов.
В общем случае в системе могут быть также связи, задаваемые отношениями R4 ⊆V4 , R5 ⊆V5 .,…, Rn ⊆Vn . Здесь n – количество элементов в системе.
Математическое представление распределенной системы
С каждым отношением связан определенный смысл, выражаемый высказыванием, например, «x следует за y», «x посылает сигнал y», «x – ребенок y и z» и т.д. Иначе говоря, вместо отношений (или вместе с отношениями) удобно рассматривать соответствующие предикаты P2 , P3 , P4 ,…, Pn . В дополнение к перечисленным рассматривают и предикаты P1, которые можно интерпретировать как выражение свойств элементов множества V.

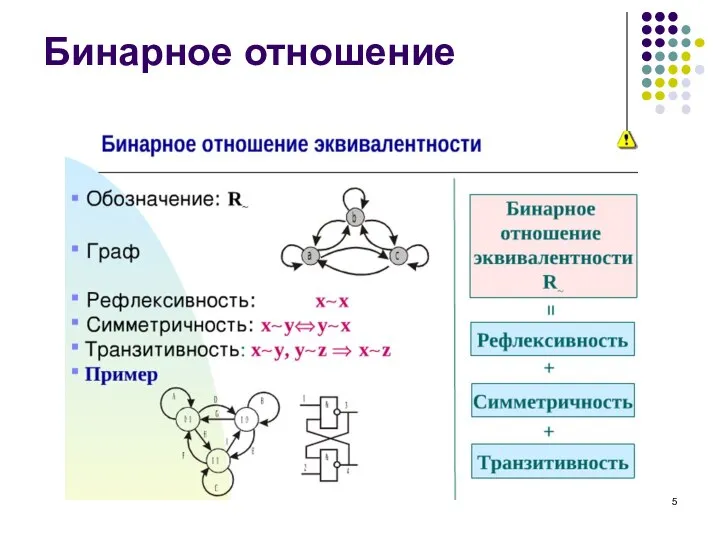
Бинарное отношение

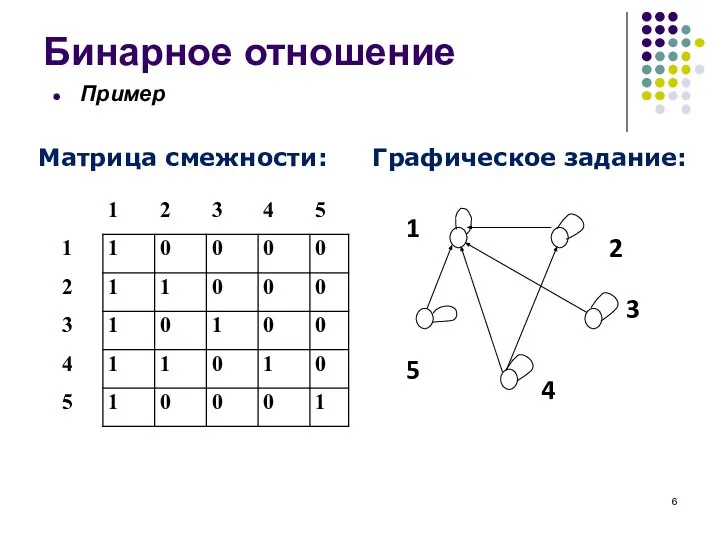
Матрица смежности:
Графическое задание:
Бинарное отношение
Пример

Подчеркнем, что бинарных отношений в системе может быть несколько. Например, в цилиндре двигателя автомобиля газ (бензино-воздушная смесь), загораясь, толкает поршень и, одновременно, нагревает его. Т.е. существует отношение «x толкает y» и отношение «x нагревает y». Ясно, что в зависимости от целей исследования системы одни отношения рассматриваются как существенные, а другие – как второстепенные.
В общем случае систему можно описать как набор
S = {V, {Pi,j}},
где
индекс i обозначает арность отношения (или количество мест предиката),
индекс j дает возможность различать отношения одной и той же арности.
Математическое представление распределенной системы

Некоторые из предикатов P1, j могут характеризовать местоположение элемента системы. Например, его географические координаты, пространственные координаты (спутник связи), нахождение в определенном помещении (компьютер локальной сети) и т.д. Подмножества элементов, имеющих одно и то же (в пределах некоторого допуска, приближения) местоположение, мы будем называть сайтами.
Аналогично, некоторые из предикатов P2, j могут характеризовать взаимное расположение элементов, например, расстояние, время передачи сигнала, стоимость переноса информации или вещества от одного элемента системы к другому. Взаимное расположение может быть существенным и для троек элементов, и для четверок и т.д., и выражаться соответствующими предикатами.
Математическое представление распределенной системы

Распределенными системами будем называть такие системы, для которых предикаты местоположения элементов или групп элементов играют существенную роль с точки зрения функционирования системы, а, следовательно, и с точки зрения анализа и синтеза системы.
Распределенные системы могут быть непрерывными и дискретными.
Непрерывные распределенные системы характеризуются бесконечным количеством элементов;
Элементы дискретной системы четко «очерчены», отделены друг от друга. Один из видов отношений – бинарное отношение «быть соседними элементами».
Математическое представление распределенной системы

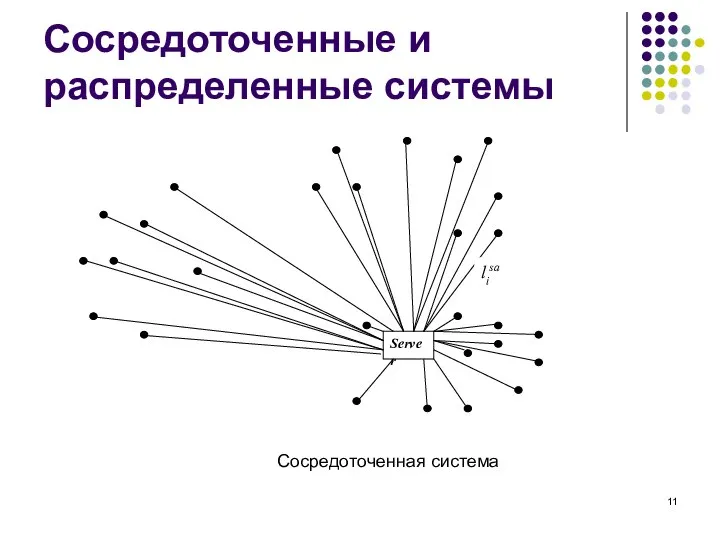
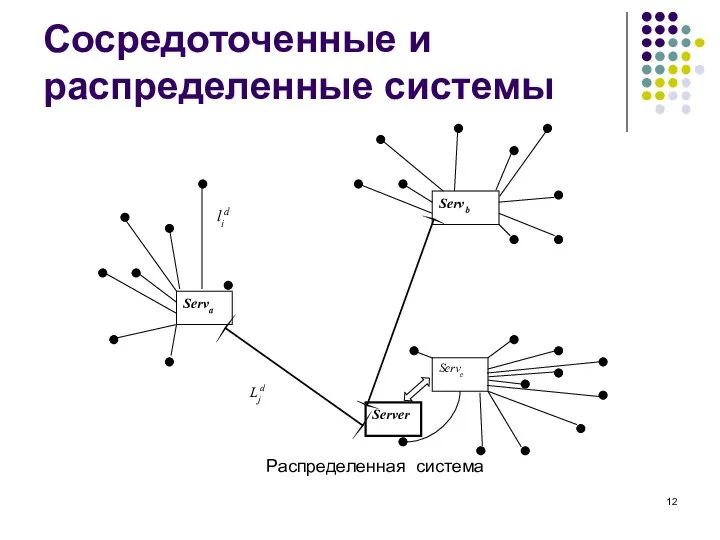
Сосредоточенные и распределенные системы
Обозначим две такие системы Sd и Ssa (от английских терминов distributed и stand-alone), тогда множество элементов в каждой из систем, обычно, можно разделить на два подмножества:
U – подмножество сосредоточенных элементов, занимающих относительно небольшой объем пространства и реализующих некоторую функцию преобразования.
W - подмножество состоящее из элементов связей элементов U между собой. Их основная задача не преобразование, а передача чего-либо в системе от одного элемента к другому.
Тогда формальное описание систем Sd и Ssa:
V(Sd) = Ud ∪ Wd
V(Ssa) = Usa ∪ Wsa

Сосредоточенные и распределенные системы
Сосредоточенная система

Сосредоточенные и распределенные системы
Распределенная система

Сосредоточенные и распределенные системы
элементы из множества Wd (связи распред. систем) могут быть весьма разнообразными, с большим количеством характеристик. Примером является передача сигналов посредством радиосвязи на сверхвысоких частотах. При этом эфир становится элементом системы. Поскольку радиоволны распространяются во всех направлениях, то эфир характеризуется тремя пространственными координатами x, y и z.
Напротив, в сосредоточенных системах элементы из множества Wsa описываются просто, а часто вообще исключаются из рассмотрения как несущественные для анализа свойств системы. Таким элементом, например, в компьютере является набор проводников, соединяющих процессор с микросхемами памяти.

Сосредоточенные и распределенные системы
Множества элементов Usa и Ud сосредоточенной и распределенной систем также могут отличаться.
В сосредоточенной системе функционирование элементов из Usa инвариантно их местоположению.
В распределенной системе функционирование элементов из Ud в общем случае зависит от их местоположения. Эта зависимость может быть нескольких видов:
1) зависимость от источников информации, имеющих определенное местоположение;
2) зависимость от поставленных задач, которые должны решаться элементами системы;
3) зависимость от параметров среды в различных точках.

Тандемы распределенных систем
Рассмотрим две системы, S1 и S2.
Первая система функционирует для достижения некоторой цели G1. При этом в любой момент времени имеется некоторая степень достижения этой цели.
Вторая система функционирует для того, чтобы ускорить достижение цели первой системой или увеличить степень достижения цели первой системой. Таким образом, система S1 является основной, а система S2 – вспомогательной.
Цель G2 создания системы S2 и/или цель ее функционирования является производной от цели G1.
Таким образом, системы S1 и S2 образуют своего рода «тандем», являющийся новой системой – фирмой с корпоративной информационной системой.

Тандемы DS
Систему S1 можно описать как набор
S1 = {V1 , {Pi, j}}, где
индекс i обозначает арность отношения (или количество мест предиката),
индекс j дает возможность различать отношения одной и той же арности.
Отдельные предикаты P1, j характеризуют местоположение элементов системы.
Некоторые из предикатов P2, j характеризуют взаимное расположение элементов.
Соответственно, система S2 описывается как набор
S2 = {V2 , {Qi, j}}.
Здесь отдельные предикаты Q1, j характеризуют местоположение элементов системы,
отдельные предикаты Q2, j характеризуют взаимное расположение элементов системы S2 .
Множество элементов V2 «порождается» множеством элементов V1 . Множества предикатов Q1, j и Q2, j «зависят» от множеств предикатов P1, j и P2, j . В частности, сайты системы S2 формируются, как правило, на основе сайтов системы S1 .

Распределенные задачи и алгоритмы
Распределенная система порождает распределенную задачу, поскольку исходные данные для задачи возникают в различных точках пространства. Также в различных точках требуются те или иные результаты решения задачи. Зачастую, задачу можно разбить на совокупность подзадач, некоторые из них могут быть сосредоточенными: все исходные данные возникают в одной точке пространства, и там же требуются результаты решения подзадачи.
Распределенная задача решается распределенным алгоритмом, собирающим исходные данные из разных точек и посылающим результаты расчетов в разные точки.

Распределенные задачи и алгоритмы
Один из видов распределенных алгоритмов – протоколы. Протокол характеризуется тем, что имеется как минимум две стороны, разделенные каналом связи. На каждой из сторон выполняется локальный (сосредоточенный) алгоритм Ak .
Локальный алгоритм A1 выполняется до некоторого момента времени, когда для продолжения работы ему требуются данные от другого локального алгоритма A2 . Он посылает через линию связи запрос на данные локальному алгоритму A2 . Алгоритм A2 отвечает, пересылая сообщение по линии связи. После этого локальный алгоритм A1 продолжает свою работу.
Протоколы, обычно, играют техническую роль и служат для установления режимов приема/передачи данных между удаленными объектами. В вычислительном отношении локальные алгоритмы – части протокола – не являются сложными.

Распределенные задачи и алгоритмы
Особый вид распределенных алгоритмов – криптографические протоколы. Они предназначены для доказательства одной или обеими сторонами, что они именно те, за кого себя выдают, для обмена конфиденциальной информацией и других подобных целей.
Рассмотрим один из простейших криптографических протоколов – распределенных алгоритмов.
Криптографические протоколы

Распределенные задачи и алгоритмы
Предположим, что в разных точках пространства находятся два объекта, O1 и O2 , каждый из которых решает свою часть (P1 и P2) общей задачи P. Вместе с тем, кроме стремления решить общую задачу, объекты имеют и свои частные задачи, Q1 и Q2 .
Таким образом, объект O1 решает одновременно задачи P1 и Q1, а объект O2 – задачи P2 и Q2 . И, если задачи P1 и P2 совместимы и взаимно дополняют друг друга, то задачи Q1 и Q2 – противоречат друг другу.
Криптографические протоколы
Следовательно, объекты O1 и O2 сотрудничают, но, одновременно, и конкурируют. А можно сказать и, что объекты конкурируют, но вынуждены сотрудничать. Смотря как расставить акценты, какая из задач, Pi или Qi , важнее для объекта Oi .

Распределенные задачи и алгоритмы
В нашей задаче объекты O1 и O2 должны прийти к общему компромиссному решению в интересах решения задачи P.
Предположим, что имеется два равноценных (с точки зрения задачи P) решения. Одно из них также устраивает объект O1, а другое – устраивает объект O2. Тогда объекты O1 и O2 решают бросить жребий, однако, бросить жребий и «увидеть» результат, находясь на большом расстоянии – весьма затруднительно.
Процедуру мог бы выполнить объект O1 и сообщить результат объекту O2. Но объект O2 не вполне доверяет объекту O1.
Выход состоит в следующем:
Криптографические протоколы

Распределенные задачи и алгоритмы
Обозначим одно из решений числом 0, другое – числом 1. Каждый из объектов независимо от другого должен назвать какое-нибудь целое число ni в пределах, например, от 0 до 99. Затем объекты обмениваются числами ni и вычисляют результат (n1 + n2 )(mod 2). Это и будет решение, т.е. число 0 или 1.
Абсолютно одновременно переслать друг другу числа ni объекты не могут. Кто-то пришлет свое число первым и окажется в невыигрышном положении. Например, O1 переслал свое число n1 объекту O2, заинтересованному в том, чтобы выиграло решение «1». Тогда O2, зная n1, решает уравнение (n1 + n2) (mod 2) = 1 относительно переменной n2, и посылает O1 найденное значение n2. Решение уравнения практически не требует времени: получив от O1 четное число, O2 должен ответить нечетным, и наоборот.
Криптографические протоколы

Распределенные задачи и алгоритмы
Эта несправедливость должна быть устранена. Ясно, что какая-то из сторон обмена сообщениями первой пришлет свое число.
Необходимо сделать так, чтобы у второй стороны не хватило времени на «подбор ответа».
Выход:
Объекты O1 и O2 могут договориться, что вся процедура «бросания жребия» на расстоянии должна завершиться за несколько минут. Если, при этом, оба объекта знают, что подбор ответа требует нескольких часов работы суперЭВМ, то они могут быть спокойны за то, что решение не «подстроено» другой стороной.
Для обеспечения таких временных параметров в вычислениях должна использоваться функция f(x), значение которой y = f(x) при известном аргументе x вычислить можно относительно быстро. Но вот решить уравнение f(y) = x, т.е. отыскать неизвестное x при известном значении y быстро нельзя. Более того, желательно, чтобы не было известно никаких математических методов для решения этого уравнения, кроме полного перебора или подобного ему по сложности.
Криптографические протоколы

Распределенные задачи и алгоритмы
Распределенный алгоритм бросания жребия состоит из шагов:
1. Объект O2 выбирает случайным образом число x из большого интервала [0, q – 1]. Вычисляет y = f(x).
2. Объект O2 пересылает число y объекту O1 . Объект O1 не сможет восстановить число x.
3. Объект O1 выбирает случайным образом число z из большого интервала [0, q – 1], и случайный бит w. Эти действия могут выполняться одновременно с п.1.
4. Объект O1 вычисляет s = h(z, y, w). Число z здесь необходимо для «маскировки» бита w, а число y – для «проверки» объектом O2 правильности действий объекта O1 .
5. Объект O1 пересылает число s объекту O2 . Бит w отправляется объекту O2 , но он «запрятан» в числе s. Объект O2 не сможет восстановить этот бит. Объект O2 не сможет восстановить и число z.
6. Объект O2 выбирает случайный бит c и отправляет его объекту O1 открытой пересылкой.
7. Объект O1 пересылает число z и бит w объекту O2 . Открытая пересылка. Объект O1 уже может определить результат бросания жребия: c + w (mod 2).
8. Объект O2 вычисляет t = h(z, y, w). Здесь z и w только что получены от O1 , а y было вычислено в п.1.
9. Объект O2 сравнивает t и s, ранее полученное от объекта O1 .
10. Если t = s, то объект O2 вычисляет результат бросания жребия: c + w (mod 2).
Криптографические протоколы

Распределенные задачи и алгоритмы
Целые числа, с которыми приходится оперировать, должны иметь в десятичной записи не менее 150-200 цифр или не менее 512 бит в двоичной записи. Такие числа называют «длинными».
Пусть f(x) и h(z, y, w) – две таких трудно обращаемых функции.
В функции h(z, y, w) первые два аргумента – длинные числа, а третий – битовый.
Функции f и h известны объектам O1 и O2 , и они владеют алгоритмами быстрого вычисления значений этих функций при заданных значениях аргументов, но не умеют быстро обращать эти функции, т.е. решать уравнения.
Криптографические протоколы (дополнительные условия)

Распределенные задачи и алгоритмы
Функции f и h могут быть различными. В частности, используются функции:
f(x) = gx (mod p) и h(z, y, w) = ywgz (mod p).
Здесь «секретные» значения x, w, z находятся в показателях степеней, и для того, чтобы найти их, требуется решить задачу дискретного логарифмирования, для которой эффективный алгоритм, существенно лучший полного перебора, неизвестен.
Константы p, q, g должны быть известны тому и другому объектам. Число p – длинное простое число. Число q – также длинное простое число, являющееся делителем числа p – 1. Число g < p, не равное 1, удовлетворяет условию
gq = (mod p).

Надежность и безопасность распределенных систем

Надежность и безопасность распределенных систем
Под надежностью понимается в соответствии с ГОСТ 27.002-89 свойство системы сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания и транспортирования.
Многие системы не являются абсолютно надежными, т.е. свойство надежности системы проявляется на конечном интервале времени эксплуатации системы, по истечении которого происходит отказ в работе. Длительность интервала безотказной работы зависит от очень большого числа факторов, предсказать которые нереально, поэтому, отказ обычно считают случайным событием.

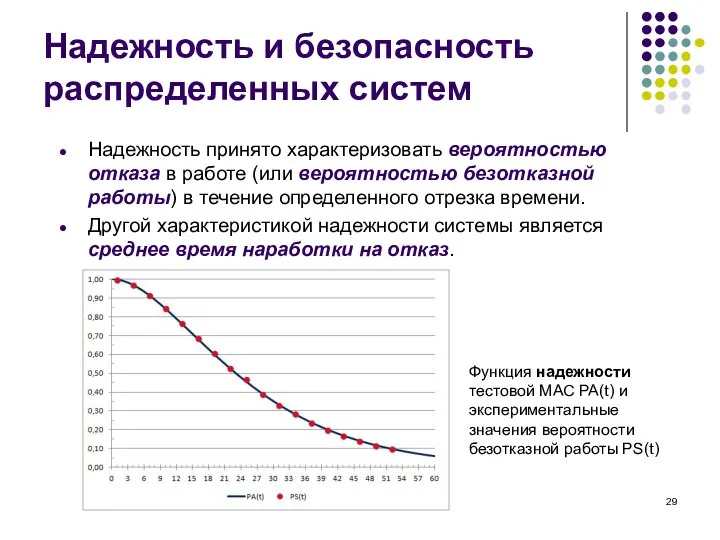
Надежность и безопасность распределенных систем
Надежность принято характеризовать вероятностью отказа в работе (или вероятностью безотказной работы) в течение определенного отрезка времени.
Другой характеристикой надежности системы является среднее время наработки на отказ.
Функция надежности тестовой МАС PA(t) и экспериментальные значения вероятности безотказной работы PS(t)

Надежность и безопасность распределенных систем
Под безопасностью понимается состояние защищенности системы от потенциально и реально существующих угроз, или отсутствие таких угроз. Система находится в состоянии безопасности, если действие внешних и внутренних факторов не приводит к ухудшению или невозможности ее функционирования.
Угрозы могут быть различного рода, в том числе угроза физического разрушения.
В контексте нашей темы интересны угрозы информационные. К ним относятся угрозы получения системой
недостоверной входной информации,
искажения внутрисистемной информации,
утечка информации о функционировании системы.

Надежность и безопасность распределенных систем
Информационная безопасность — состояние защищенности информационной среды общества, обеспечивающее ее формирование, использование и развитие в интересах граждан, организаций, государства.
В качестве стандартной модели безопасности часто приводят модель CIA:
конфиденциальность информации – confidentiality (обязательное для выполнения лицом, получившим доступ к определенной информации, требование не передавать такую информацию третьим лицам без согласия ее владельца);
целостность (integrity) - гарантия существования информации в непротиворечивом виде;
доступность (availability) - возможность получение информации авторизованным пользователем в нужное для него время.

Надежность и безопасность распределенных систем
Выделяют и другие категории безопасности:
аутентичность — возможность установления автора информации;
апеллируемость — возможность доказать что автором является именно заявленный человек, и не никто другой.
Все физические элементы любой системы являются потенциально ненадежными и уязвимыми с точки зрения безопасности.

Надежность и безопасность распределенных систем
Ненадежность элементов системы, осуществляющих переработку информации, может заключаться
в полном отказе от переработки,
в изменении функции (стабильном получении неверных результатов),
в сбоях (периодическом возникновении ошибок).
в полном прекращении передачи, в одностороннем прекращении передачи (для двунаправленных каналов),
в возникновении случайных ошибок при передаче (помех).

Надежность и безопасность распределенных систем
Таким образом, проблемы надежности и безопасности во многом родственны. Они связаны с вмешательством в функционирование системы. Различие заключается в том, что ненадежность определяется физическими, природными факторами и не связана с чьими-то целями.
Небезопасность определяется, в основном, «человеческим фактором» - наличием злоумышленников и/или беспечных сотрудников. Но одна из проблем безопасности – утечка информации при несанкциони-рованном доступе – не имеет аналога среди проблем надежности.

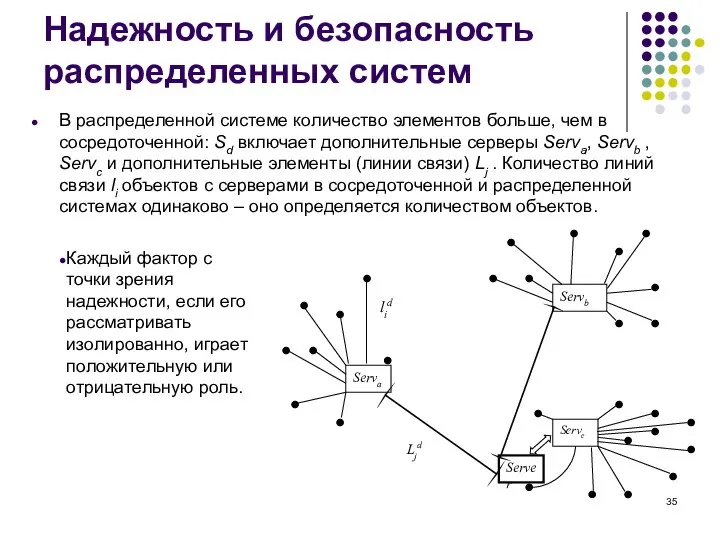
Надежность и безопасность распределенных систем
В распределенной системе количество элементов больше, чем в сосредоточенной: Sd включает дополнительные серверы Serva, Servb , Servc и дополнительные элементы (линии связи) Lj . Количество линий связи li объектов с серверами в сосредоточенной и распределенной системах одинаково – оно определяется количеством объектов.
Каждый фактор с точки зрения надежности, если его рассматривать изолированно, играет положительную или отрицательную роль.

Надежность и безопасность распределенных систем
Негативно влияет на надежность:
увеличение количества ненадежных элементов в системе при прочих равных условиях играет отрицательную роль. Под прочими равными условиями здесь понимается
неизменность архитектуры (соединений и распределения функций) системы,
неизменность параметров элементов и проч.
Если же архитектуру изменить, например, использовать дополнительные элементы для дублирования (резервирования), то надежность, напротив, повышается.
Увеличение длины линий связи: Обычно с увеличением длины линии увеличивается
количество помех,
стоимость передачи,
возможности злоумышленников по съему информации или по ее искажению.

Методики построения алгоритмов для обеспечения надежности DS
Все эти факторы надо учитывать при разработке методики построения алгоритмов:
Она должна быть рассчитана на возможные сбои или рассогласования в работе узлов системы (при программировании в сосредоточенных системах возможность сбоя обычно не учитывается).
В настоящее время существует два подхода к разработке распределенных алгоритмов:
построение отказоустойчивых алгоритмов и
построение стабилизирующих алгоритмов.
В устойчивых алгоритмах каждый шаг каждого процесса предпринимается с достаточной осторожностью, чтобы гарантировать, что, несмотря на сбои, правильные процессы выполняют только правильные шаги.
В стабилизирующих алгоритмах правильные процессы могу быть подвержены сбоям, но алгоритм в целом гарантирует исправление ошибок.

Устойчивые алгоритмы
Разработаны так, чтобы учитывать возможность сбоев в некоторых процессах (относительно небольшом их количестве) и гарантировать при этом правильность выполнения тех процессов, в которых не произошло сбоев.
Эти алгоритмы используют такие стратегии как голосование, вследствие чего процесс воспримет только такую информацию извне, о получении которой объявит достаточно много других процессов. Однако процесс никогда не должен ждать получения информации от всех процессов, потому что может возникнуть тупик, если при выполнении какого-либо процесса произойдет сбой.
Устойчивые алгоритмы защищают систему от отказов ограниченного числа узлов. Остающиеся работоспособными узлы поддерживают правильное (хотя возможно менее эффективное) поведение во время восстановления и реконфигурации системы.
Следовательно, устойчивые алгоритмы должны использоваться, когда невозможно временное прерывание работы.

Стабилизирующие алгоритмы
Предлагают защиту против временных сбоев, то есть, временного аномального поведения компонент системы. Эти сбои могут происходить в больших частях распределенной системы, когда физические условия временно достигают критических значений, стимулируя ошибочное поведение памяти и процессоров.
Примером может быть система управления космической станцией, когда станция подвергается сильному космическому излучению, а также системы, в которых на многие компоненты одновременно воздействуют неблагоприятные природные условия. Когда воздействие этих условий исчезает, процессы восстанавливают свою работоспособность и функционируют на основе программ. Однако из-за их временного аномального поведения глобальное результирующее состояние системы может быть непредвиденным. Свойство стабилизации гарантирует сходимость к требуемому поведению.

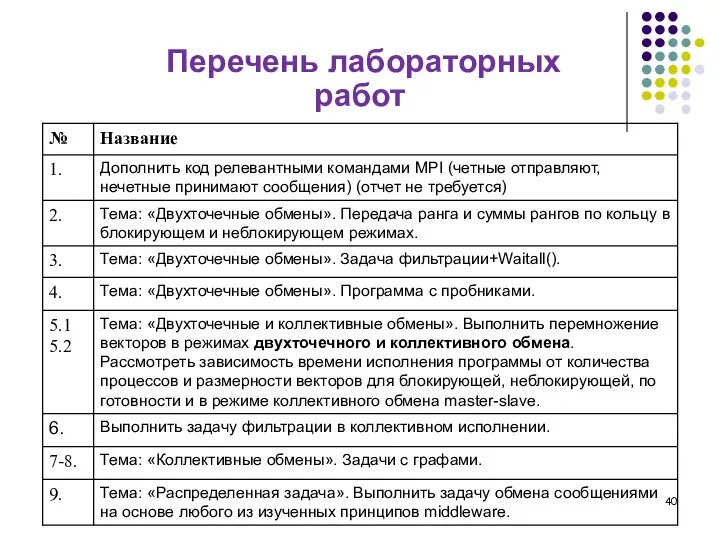
Перечень лабораторных работ