Слайд 2Формулировка задачи 3.33
Рассматривается информация о стоимости коттеджей в Московской области по Киевскому

направлению (по данным строительной компании «Стройсервис», осень 1997 г.)
Данные находятся в файле villa.xls. Переменные описаны в таблице 3.28.
Подберите функциональную форму зависимости цены коттеджа от его параметров, учитывая такие факторы, как t-статистика и коэффициент детерминации R^2
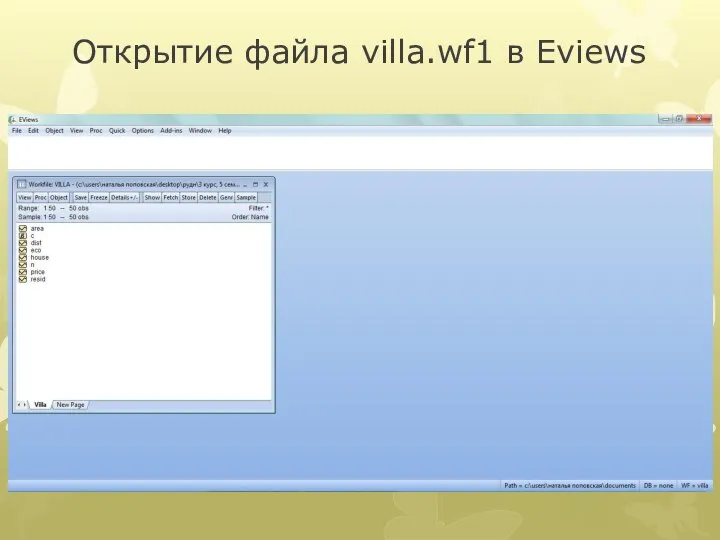
Слайд 3Открытие файла villa.wf1 в Eviews
Слайд 4Построение описательной статистики [1]
![Построение описательной статистики [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-3.jpg)
Слайд 5Построение описательной статистики [2]
![Построение описательной статистики [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-4.jpg)
Слайд 6Построение описательной статистики [3]
![Построение описательной статистики [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-5.jpg)
Слайд 7Построение описательной статистики [4]
![Построение описательной статистики [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-6.jpg)
Слайд 8Сохранение через Freeze->Name [1]
![Сохранение через Freeze->Name [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-7.jpg)
Слайд 9Сохранение через Freeze->Name [2]
![Сохранение через Freeze->Name [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-8.jpg)
Слайд 10Сохранение через Freeze->Name [3]
![Сохранение через Freeze->Name [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-9.jpg)
Слайд 11Сохранение через Freeze->Name [4]
![Сохранение через Freeze->Name [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-10.jpg)
Слайд 12Построение корреляционной матрицы [1]
![Построение корреляционной матрицы [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-11.jpg)
Слайд 13Построение корреляционной матрицы [2]
![Построение корреляционной матрицы [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-12.jpg)
Слайд 14Построение корреляционной матрицы [3]
![Построение корреляционной матрицы [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-13.jpg)
Слайд 15Построение корреляционной матрицы [4]
![Построение корреляционной матрицы [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-14.jpg)
Слайд 16Построение корреляционной матрицы [5]
![Построение корреляционной матрицы [5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-15.jpg)
Слайд 17Построение диаграммы рассеяния [1, house-price]
![Построение диаграммы рассеяния [1, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-16.jpg)
Слайд 18Построение диаграммы рассеяния [2, house-price]
![Построение диаграммы рассеяния [2, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-17.jpg)
Слайд 19Построение диаграммы рассеяния [3, house-price]
![Построение диаграммы рассеяния [3, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-18.jpg)
Слайд 20Построение диаграммы рассеяния [4, house-price]
![Построение диаграммы рассеяния [4, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-19.jpg)
Слайд 21Построение диаграммы рассеяния [5, house-price]
![Построение диаграммы рассеяния [5, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-20.jpg)
Слайд 22Создание lnprice и lnhouse в командной строке командой genr lnprice=log(price) и genr
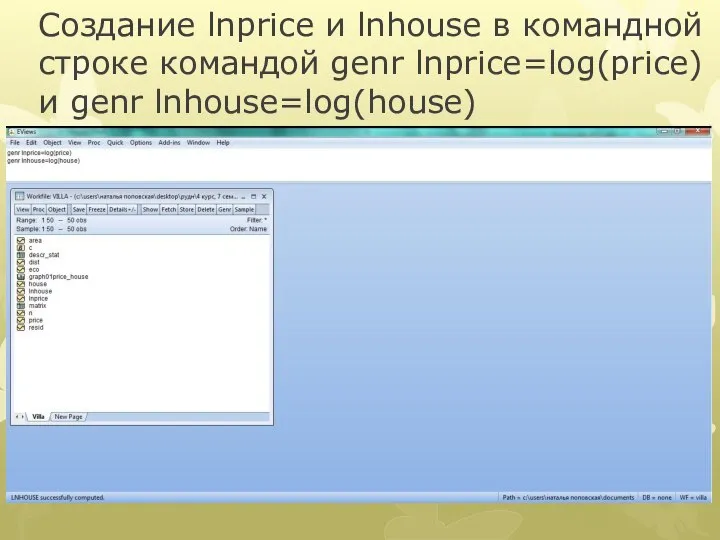
lnhouse=log(house)
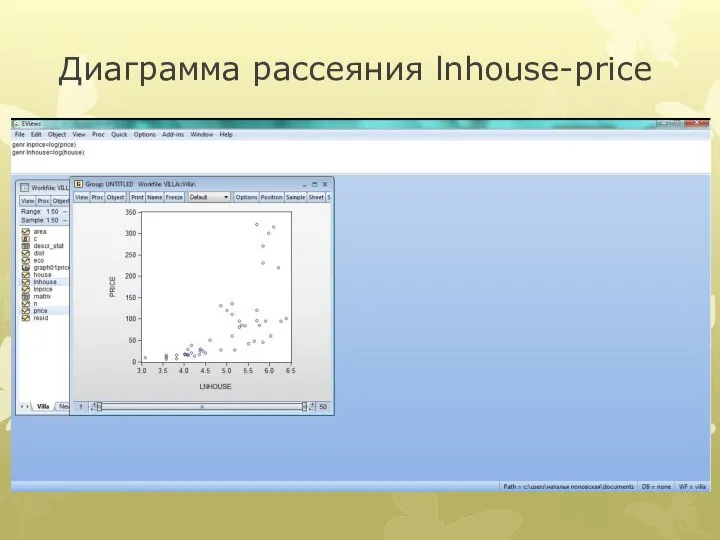
Слайд 23Диаграмма рассеяния lnhouse-price
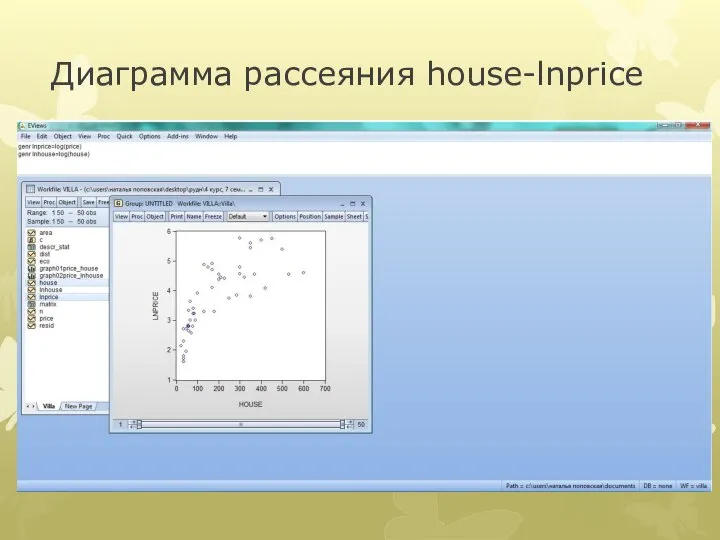
Слайд 24Диаграмма рассеяния house-lnprice
Слайд 25Диаграмма рассеяния lnhouse-lnprice
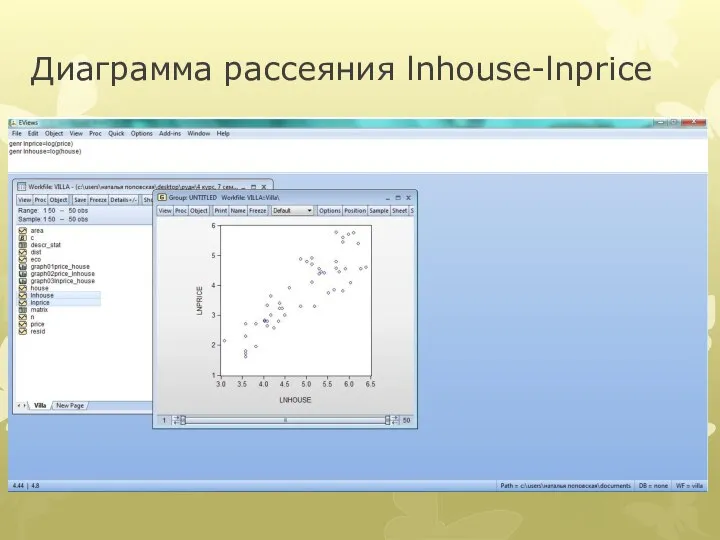
Слайд 26
Проанализировав диаграммы рассеяния, мы приходим к выводу, что самой хорошей функциональной
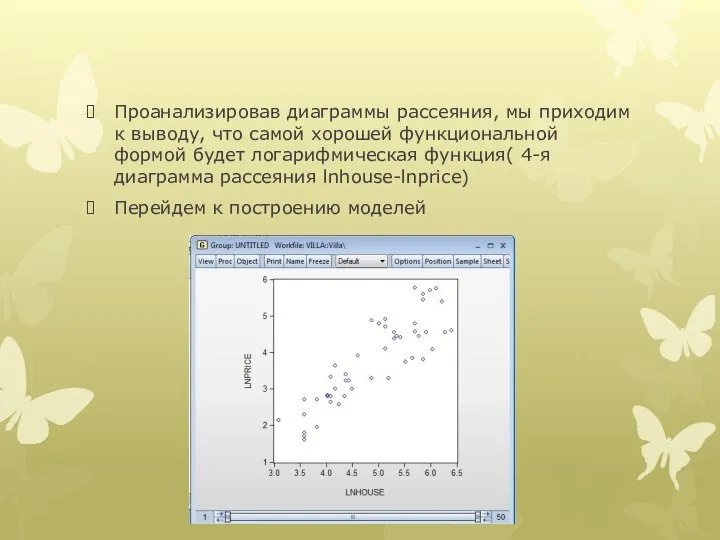
формой будет логарифмическая функция( 4-я диаграмма рассеяния lnhouse-lnprice)
Перейдем к построению моделей
Слайд 271. Линейная модель. Построение [1]
![1. Линейная модель. Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-26.jpg)
Слайд 281. Линейная модель. Построение [2]
![1. Линейная модель. Построение [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-27.jpg)
Слайд 291. Линейная модель. Построение [3]
В линейную модель включаем переменные без логарифмов. Все
![1. Линейная модель. Построение [3] В линейную модель включаем переменные без логарифмов. Все коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-28.jpg)
коэффициенты значимы (Prob<0.05, у Const не учитываем).R^2=0,631855, adj ^2=0.599131, модель значима
Слайд 301. Линейная модель
Вывод уравнения [1]
![1. Линейная модель Вывод уравнения [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-29.jpg)
Слайд 311. Линейная модель
Вывод уравнения [2]. Интерпретация [1]
y= β0+β1x1+β2x2+…+βnxn
При возрастании xj на 1
![1. Линейная модель Вывод уравнения [2]. Интерпретация [1] y= β0+β1x1+β2x2+…+βnxn При возрастании](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-30.jpg)
единицу (своего измерения), у возрастает на βj единиц (своего измерения)
Слайд 321. Линейная модель. Интерпретация [2]
dist – при увеличении расстояния на 1 км
![1. Линейная модель. Интерпретация [2] dist – при увеличении расстояния на 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-31.jpg)
цена коттеджа падает на 739$
house – при увеличении площади дома на 1 кв.м цена коттеджа увеличивается на 175$
Слайд 331. Линейная модель. Интерпретация [3]
eco – если рядом есть реки и озера,
![1. Линейная модель. Интерпретация [3] eco – если рядом есть реки и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-32.jpg)
то цена возрастает на 42 тыс $
area – при увеличении площади участка на 1 сотку цена увеличивается на 3462 $
Слайд 342. Полулогарифмическая модель (log(y)). Построение [1]
![2. Полулогарифмическая модель (log(y)). Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-33.jpg)
Слайд 352. Полулогарифмическая модель (log(y)). Построение [2]
![2. Полулогарифмическая модель (log(y)). Построение [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-34.jpg)
Слайд 362. Полулогарифмическая модель (log(y)). Построение [3]
Коэффициенты значимы (Prob<0.05), R^2=0.782721, adjR^2=0.763408, заметим, что
![2. Полулогарифмическая модель (log(y)). Построение [3] Коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-35.jpg)
они выше, чем у линейной модели. Модель значима.
Слайд 372. Полулогарифмическая модель (log(y)). Вывод уравнения. Интерпретация [1]
ln(y)= β0+β1x1+β2x2+…+βnxn
При изменении xj на
![2. Полулогарифмическая модель (log(y)). Вывод уравнения. Интерпретация [1] ln(y)= β0+β1x1+β2x2+…+βnxn При изменении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-36.jpg)
1 единицу, y меняется на (e^ βj -1)*100% (при малых -0.2< βj <0.2 это примерно равно βj *100%)
Слайд 382. Полулогарифмическая модель (log(y)). Интерпретация [2]
house - при изменении площади дома на
![2. Полулогарифмическая модель (log(y)). Интерпретация [2] house - при изменении площади дома](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-37.jpg)
1 кв.м цена меняется на 0.29% (т.к. -0.2<βj<0.2)
eco – если рядом есть реки и озера, то цена увеличивается на 55%
Слайд 392. Полулогарифмическая модель (log(y)). Интерпретация [3]
dist – при увеличении расстояния на 1
![2. Полулогарифмическая модель (log(y)). Интерпретация [3] dist – при увеличении расстояния на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-38.jpg)
км цена снижается на 1.6% (т.к. -0.2<βj<0.2)
area – при увеличении площади участка на 1 сотку цена меняется на 3.6%
Слайд 403. Полулогарифмическая модель (log(x)). Построение [1]
![3. Полулогарифмическая модель (log(x)). Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-39.jpg)
Слайд 413. Полулогарифмическая модель (log(x)). Построение [2]
Коэффициенты значимы (Prob<0.05, у Const не учитываем).
![3. Полулогарифмическая модель (log(x)). Построение [2] Коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-40.jpg)
R^2=0.641281, adj R^2=0.609395, заметим, что R^2 ниже, чем у полулогарифмической (log(y)) , но выше, чем у линейной. Модель значима.
Слайд 423. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [1]
y= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn)
При измененииxj на 1
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [1] y= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn) При измененииxj](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-41.jpg)
%, у меняется в среднем на βj/100 единиц измерения
Слайд 433. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [2]
house – при увеличении площади
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [2] house – при увеличении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-42.jpg)
дома на 1 кв.м цена увеличивается на 0.24 тыс $
dist – при увеличении расстояния на 1 км цена уменьшится на 0.36 тыс $
Слайд 443. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [3]
area – при увеличении площади
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [3] area – при увеличении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-43.jpg)
участка на 1 сотку цена увеличится на 0.6 тыс $
eco – если рядом есть реки и озера, то цена увеличивается на 40 тыс $ (у eco не стоит log, т.к. принимает значения только 0 и 1)
Слайд 454. Логарифмическая модель. Построение [1]
![4. Логарифмическая модель. Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-44.jpg)
Слайд 464. Логарифмическая модель. Построение [2]
Мы не взяли в модель eco, т.к. это
![4. Логарифмическая модель. Построение [2] Мы не взяли в модель eco, т.к.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-45.jpg)
фиктивная переменная (принимает значения только 0 и 1)Коэффициенты значимы (Prob<0.05, у Const не учитываем). R^2=0.821542, adjR^2=0.809904, коэффициенты выше, чем у других моделей. Модель значима.
Слайд 474. Логарифмическая модель. Интерпретация [1]
ln(y)= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn)
При изменении xj на 1 %, у
![4. Логарифмическая модель. Интерпретация [1] ln(y)= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn) При изменении xj на 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-46.jpg)
меняется на βj %
Слайд 484. Логарифмическая модель. Интерпретация [2]
house – при увеличении площади дома на 1
![4. Логарифмическая модель. Интерпретация [2] house – при увеличении площади дома на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-47.jpg)
% цена увеличивается на 0.79 %
dist – при увеличении расстояния на 1 % цена уменьшается на 0.36 %
area – при увеличении площади участка на 1 % цена увеличится на 0.45 %
Слайд 49Проверка логарифмической модели на гетероскедастичноcть[1]
![Проверка логарифмической модели на гетероскедастичноcть[1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-48.jpg)
Слайд 50Проверка логарифмической модели на гетероскедастичноcть[2]
Выбираем проверку по White.
![Проверка логарифмической модели на гетероскедастичноcть[2] Выбираем проверку по White.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-49.jpg)
Слайд 51Проверка логарифмической модели на гетероскедастичноcть[3]
Гетероскедастичность – непостоянство дисперсии остатков
H0: Остатки гомоскедастичны, σ^2=Const
H1:
![Проверка логарифмической модели на гетероскедастичноcть[3] Гетероскедастичность – непостоянство дисперсии остатков H0: Остатки](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-50.jpg)
Остатки гетероскедастичны σ^2 ≠ Const.
Присутствуют Prob.<0.05, значит принимает гипотезу H1 (гетероскедастичность есть), смотрим коэффициент Durbin-Watson, сравниваем с 1.5( 2.239053>1.5)
Слайд 54Подправка [3]
Т.к. коэффициент Durbin-Watson>1.5, то берем подправку по White, в ином случае(D-W<1.5)
![Подправка [3] Т.к. коэффициент Durbin-Watson>1.5, то берем подправку по White, в ином случае(D-W](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-53.jpg)
– Newey-West.
Слайд 55Подправка [4]
Probability log(area) и log(dist) стали ближе к нулю, то есть стали
![Подправка [4] Probability log(area) и log(dist) стали ближе к нулю, то есть стали лучше значимости коэффициентов.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-54.jpg)
лучше значимости коэффициентов.


![Построение описательной статистики [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-3.jpg)
![Построение описательной статистики [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-4.jpg)
![Построение описательной статистики [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-5.jpg)
![Построение описательной статистики [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-6.jpg)
![Сохранение через Freeze->Name [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-7.jpg)
![Сохранение через Freeze->Name [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-8.jpg)
![Сохранение через Freeze->Name [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-9.jpg)
![Сохранение через Freeze->Name [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-10.jpg)
![Построение корреляционной матрицы [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-11.jpg)
![Построение корреляционной матрицы [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-12.jpg)
![Построение корреляционной матрицы [3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-13.jpg)
![Построение корреляционной матрицы [4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-14.jpg)
![Построение корреляционной матрицы [5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-15.jpg)
![Построение диаграммы рассеяния [1, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-16.jpg)
![Построение диаграммы рассеяния [2, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-17.jpg)
![Построение диаграммы рассеяния [3, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-18.jpg)
![Построение диаграммы рассеяния [4, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-19.jpg)
![Построение диаграммы рассеяния [5, house-price]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-20.jpg)





![1. Линейная модель. Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-26.jpg)
![1. Линейная модель. Построение [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-27.jpg)
![1. Линейная модель. Построение [3] В линейную модель включаем переменные без логарифмов. Все коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-28.jpg)
![1. Линейная модель Вывод уравнения [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-29.jpg)
![1. Линейная модель Вывод уравнения [2]. Интерпретация [1] y= β0+β1x1+β2x2+…+βnxn При возрастании](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-30.jpg)
![1. Линейная модель. Интерпретация [2] dist – при увеличении расстояния на 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-31.jpg)
![1. Линейная модель. Интерпретация [3] eco – если рядом есть реки и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-32.jpg)
![2. Полулогарифмическая модель (log(y)). Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-33.jpg)
![2. Полулогарифмическая модель (log(y)). Построение [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-34.jpg)
![2. Полулогарифмическая модель (log(y)). Построение [3] Коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-35.jpg)
![2. Полулогарифмическая модель (log(y)). Вывод уравнения. Интерпретация [1] ln(y)= β0+β1x1+β2x2+…+βnxn При изменении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-36.jpg)
![2. Полулогарифмическая модель (log(y)). Интерпретация [2] house - при изменении площади дома](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-37.jpg)
![2. Полулогарифмическая модель (log(y)). Интерпретация [3] dist – при увеличении расстояния на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-38.jpg)
![3. Полулогарифмическая модель (log(x)). Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-39.jpg)
![3. Полулогарифмическая модель (log(x)). Построение [2] Коэффициенты значимы (Prob](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-40.jpg)
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [1] y= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn) При измененииxj](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-41.jpg)
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [2] house – при увеличении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-42.jpg)
![3. Полулогарифмическая модель (log(x)). Вывод уравнения. Интерпретация [3] area – при увеличении](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-43.jpg)
![4. Логарифмическая модель. Построение [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-44.jpg)
![4. Логарифмическая модель. Построение [2] Мы не взяли в модель eco, т.к.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-45.jpg)
![4. Логарифмическая модель. Интерпретация [1] ln(y)= β0+β1ln(x1)+β2ln(x2)+…+βnln(xn) При изменении xj на 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-46.jpg)
![4. Логарифмическая модель. Интерпретация [2] house – при увеличении площади дома на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-47.jpg)
![Проверка логарифмической модели на гетероскедастичноcть[1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-48.jpg)
![Проверка логарифмической модели на гетероскедастичноcть[2] Выбираем проверку по White.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-49.jpg)
![Проверка логарифмической модели на гетероскедастичноcть[3] Гетероскедастичность – непостоянство дисперсии остатков H0: Остатки](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-50.jpg)
![Подправка [1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-51.jpg)
![Подправка [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-52.jpg)
![Подправка [3] Т.к. коэффициент Durbin-Watson>1.5, то берем подправку по White, в ином случае(D-W](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-53.jpg)
![Подправка [4] Probability log(area) и log(dist) стали ближе к нулю, то есть стали лучше значимости коэффициентов.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-54.jpg)
![Проверка на нормальность[1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/959293/slide-55.jpg)
 Правила вычисления производных
Правила вычисления производных Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл ЕГЭ. Экономические задачи IV
ЕГЭ. Экономические задачи IV Построение сечений
Построение сечений Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов
Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Старинные задачи на дроби
Старинные задачи на дроби Презентация на тему Что такое функция? 7 класс
Презентация на тему Что такое функция? 7 класс  Правильные многогранник. Повторение
Правильные многогранник. Повторение Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Степени и логарифмы
Степени и логарифмы Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами
Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Вычитание. Решение текстовых задач с помощью сложения и вычитания
Вычитание. Решение текстовых задач с помощью сложения и вычитания Занимательная геометрия (1 класс)
Занимательная геометрия (1 класс) Исследование на принадлежность классам функцию. Практическая работа
Исследование на принадлежность классам функцию. Практическая работа Перпендикулярные прямые
Перпендикулярные прямые Обратные тригонометрические функции
Обратные тригонометрические функции Случайные величины 14 сен
Случайные величины 14 сен Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Решаем практическую задачу
Решаем практическую задачу Загадки и тайны треугольника
Загадки и тайны треугольника Параллелограмм
Параллелограмм Признаки параллельности прямых
Признаки параллельности прямых Геометрический материал
Геометрический материал Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой