Кривые линии. Комплексный чертеж поверхности

содержание лекции
кривые линии
поверхности
поверхности вращения
способы задания поверхности на чертеже
классификация поверхностей
условия принадлежности точки и линии поверхности
точки на цилиндре вращения
точки на сфере
точки на конусе вращения
построение линий на поверхностях

КРИВЫЕ ЛИНИИ

кривая линия
множество точек пространства,
координаты которых – функции одной переменной

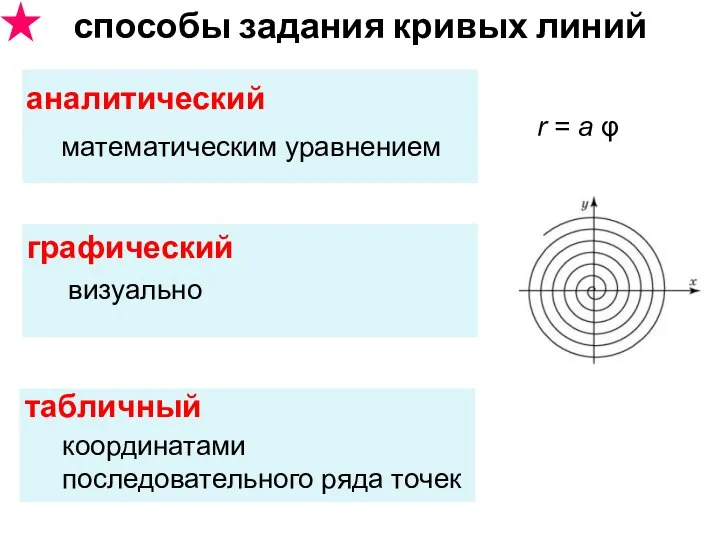
способы задания кривых линий
аналитический
графический
табличный
математическим уравнением
визуально
координатами
последовательного ряда точек
r = a φ

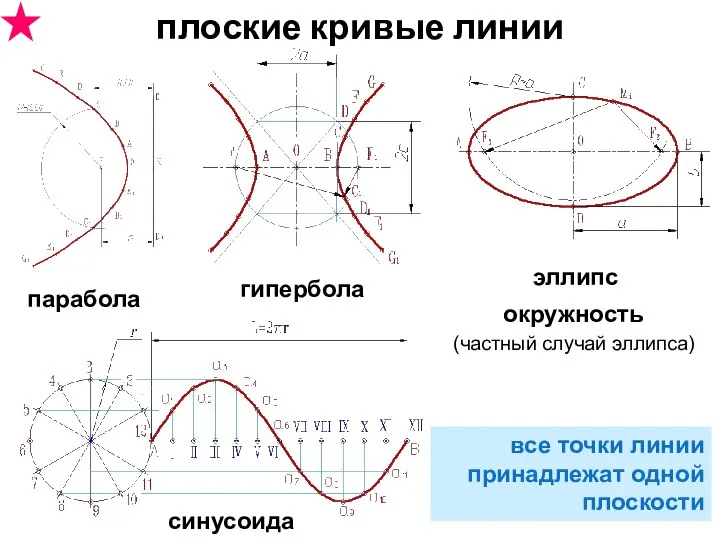
(частный случай эллипса)
плоские кривые линии
парабола
гипербола
эллипс
окружность
синусоида
все точки линии принадлежат одной плоскости

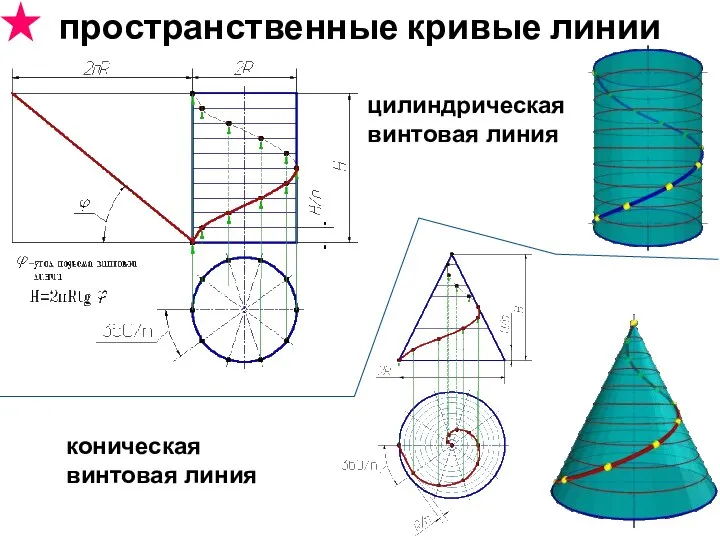
цилиндрическая винтовая линия
пространственные кривые линии
коническая
винтовая линия

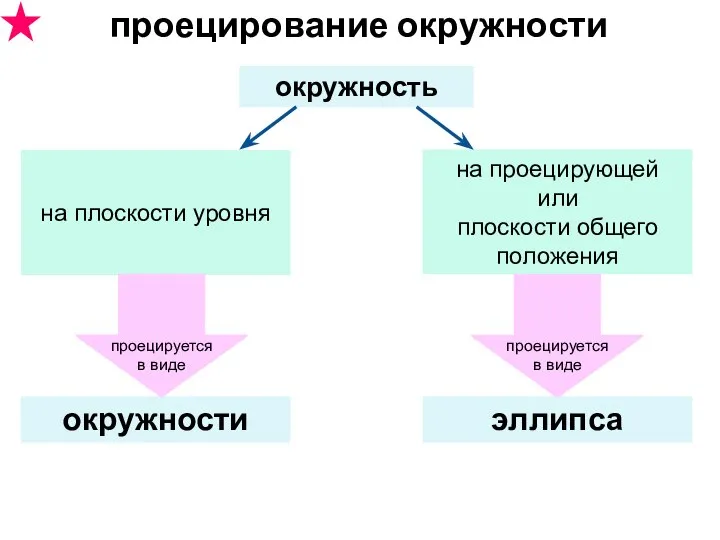
эллипса
проецирование окружности
окружность
окружности
на плоскости уровня
на проецирующей
или
плоскости общего положения

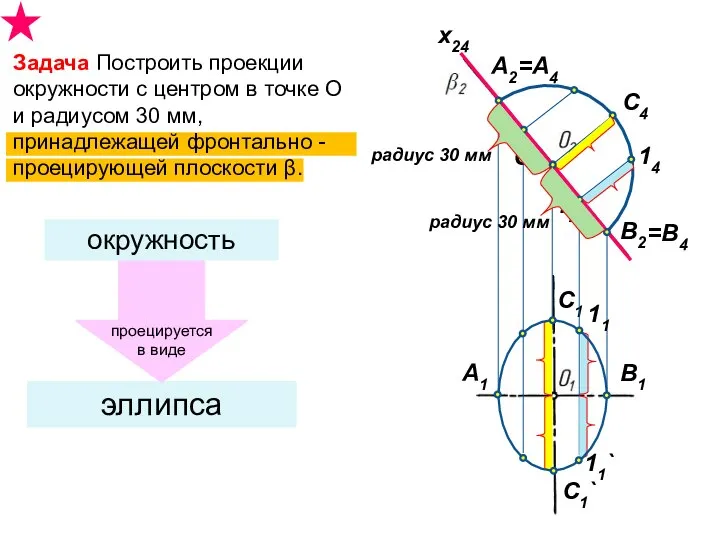
Задача Построить проекции
окружности с центром в точке О
и радиусом 30 мм,
принадлежащей фронтально -проецирующей плоскости β.
12
А2
B2
C4
А1
B1
C1
C1`
C2
=B4
=А4
x24
14
11
11`
радиус 30 мм
радиус 30 мм

ПОВЕРХНОСТИ

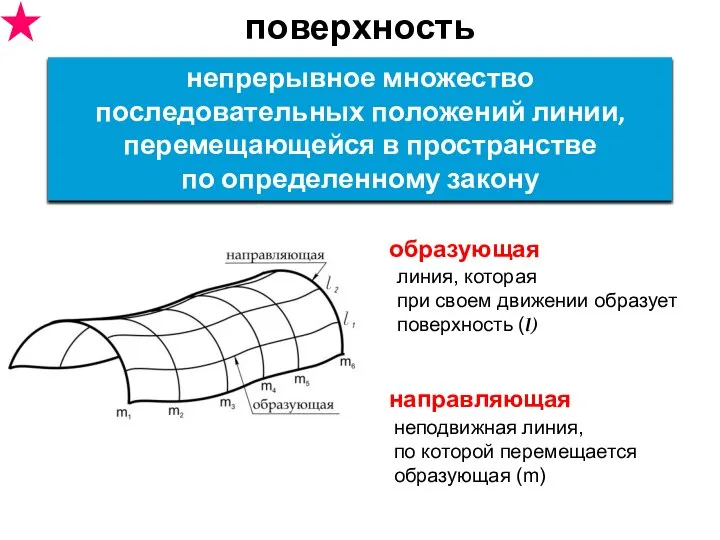
поверхность
неподвижная линия,
по которой перемещается образующая (m)
непрерывное множество
последовательных положений линии,
перемещающейся в пространстве
по определенному закону
образующая
линия, которая
при своем движении образует поверхность (l)
направляющая

способы задания поверхности на чертеже
1. каркас
2. определитель
3. очерк

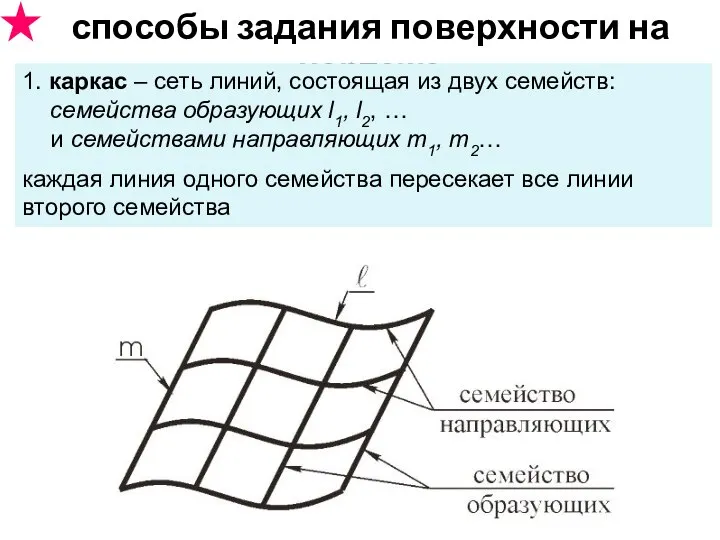
способы задания поверхности на чертеже
1. каркас – сеть линий, состоящая из двух семейств:
семейства образующих l1, l2, …
и семействами направляющих m1, m2…
каждая линия одного семейства пересекает все линии второго семейства

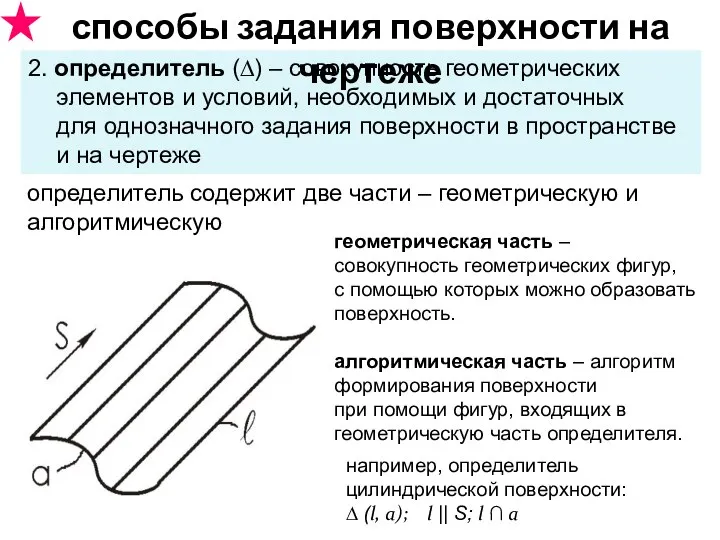
например, определитель цилиндрической поверхности:
∆ (l, а); l || S; l ∩ а
2. определитель (∆) – совокупность геометрических элементов и условий, необходимых и достаточных
для однозначного задания поверхности в пространстве и на чертеже
способы задания поверхности на чертеже
геометрическая часть –
совокупность геометрических фигур,
с помощью которых можно образовать поверхность.
алгоритмическая часть – алгоритм формирования поверхности
при помощи фигур, входящих в геометрическую часть определителя.
определитель содержит две части – геометрическую и алгоритмическую

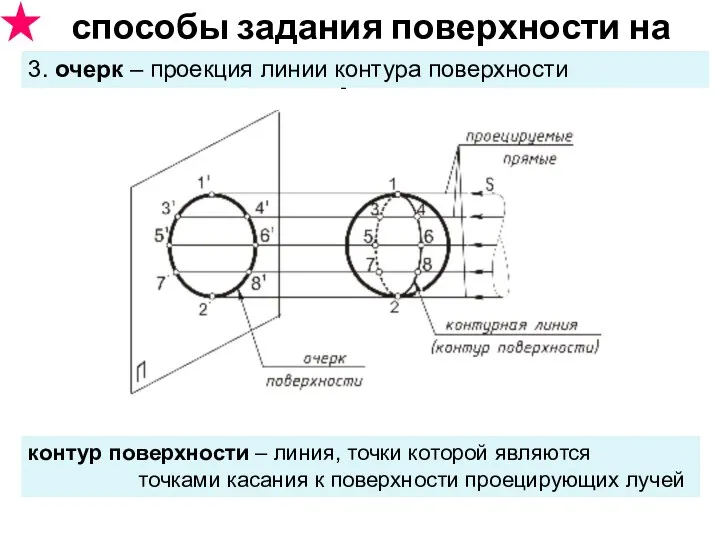
способы задания поверхности на чертеже
3. очерк – проекция линии контура поверхности
контур поверхности – линия, точки которой являются
точками касания к поверхности проецирующих лучей

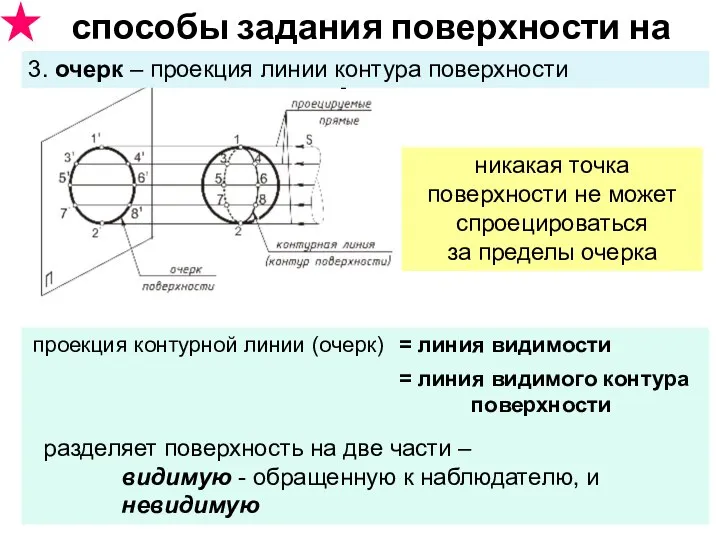
способы задания поверхности на чертеже
3. очерк – проекция линии контура поверхности
никакая точка поверхности не может спроецироваться
за пределы очерка
проекция контурной линии (очерк)
разделяет поверхность на две части –
видимую - обращенную к наблюдателю, и невидимую
= линия видимости
= линия видимого контура поверхности

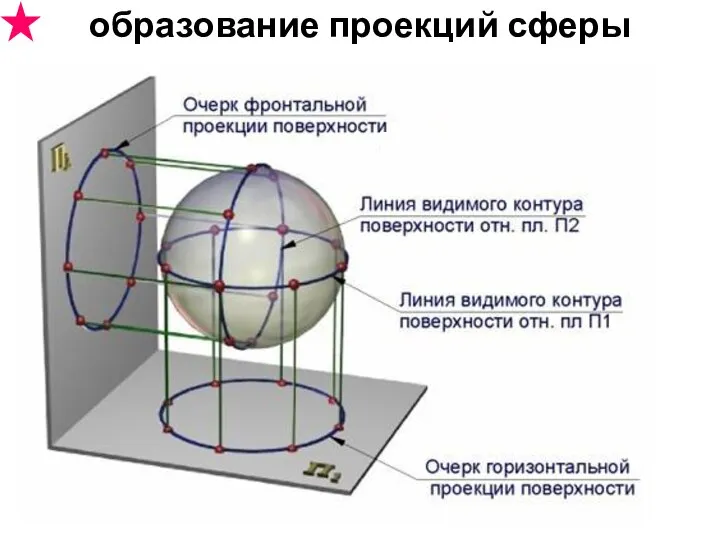
образование проекций сферы

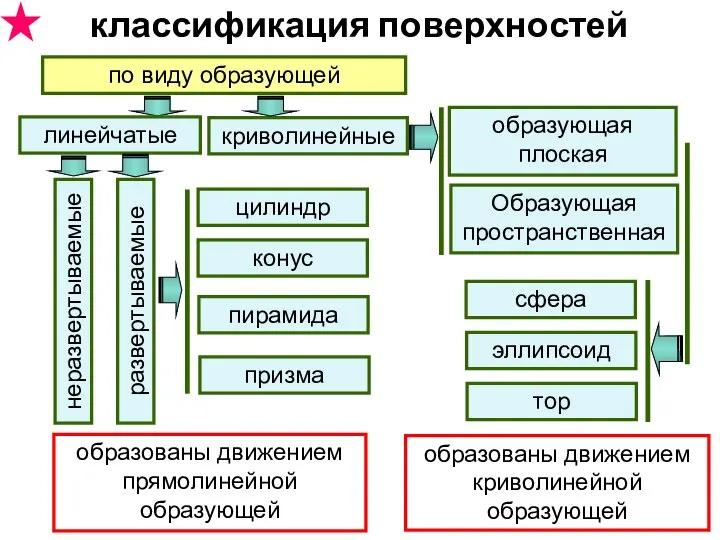
по виду образующей:
1. линейчатые поверхности – с прямолинейной образующей
2. нелинейчатые – с криволинейной образующей
по закону движения образующей: (т. е. по направляющей)
1. поверхности вращения
2. винтовые поверхности
3. поверхности с плоскостью параллелизма (поверхности Каталана)
классификация поверхностей

по виду образующей
линейчатые
криволинейные
развертываемые
неразвертываемые
цилиндр
конус
пирамида
призма
образующая плоская
Образующая пространственная
сфера
эллипсоид
тор
образованы движением прямолинейной образующей
образованы движением криволинейной образующей
классификация поверхностей

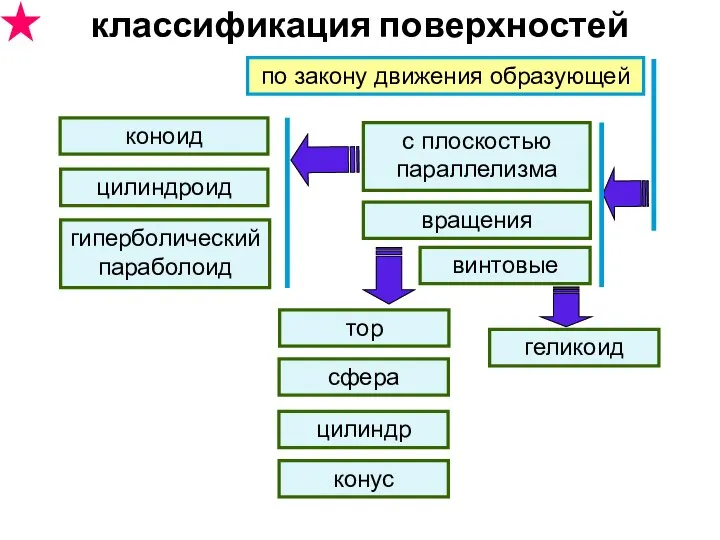
по закону движения образующей
с плоскостью параллелизма
вращения
винтовые
конус
цилиндр
сфера
тор
коноид
цилиндроид
гиперболический параболоид
геликоид
классификация поверхностей

ПОВЕРХНОСТИ ВРАЩЕНИЯ

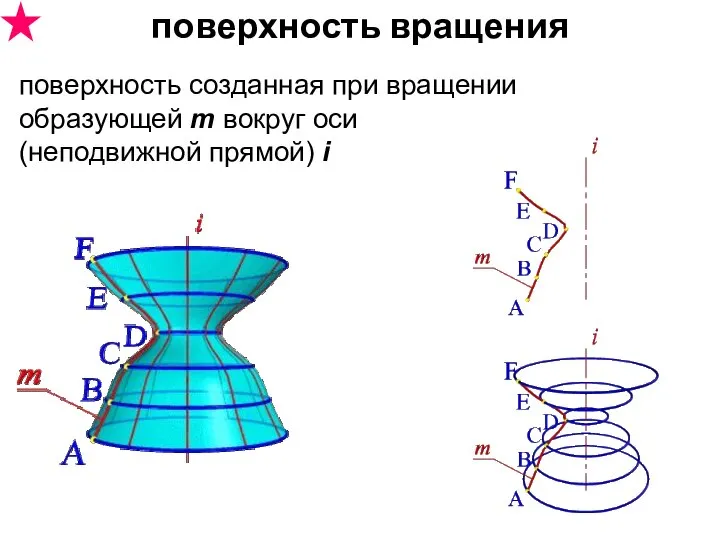
поверхность созданная при вращении образующей m вокруг оси
(неподвижной прямой) i
поверхность вращения

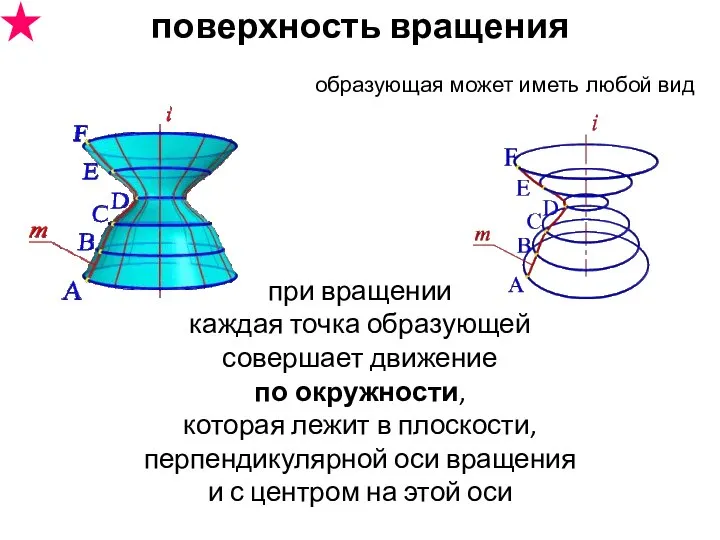
образующая может иметь любой вид
при вращении
каждая точка образующей
совершает движение
по окружности,
которая лежит в плоскости,
перпендикулярной оси вращения
и с центром на этой оси
поверхность вращения

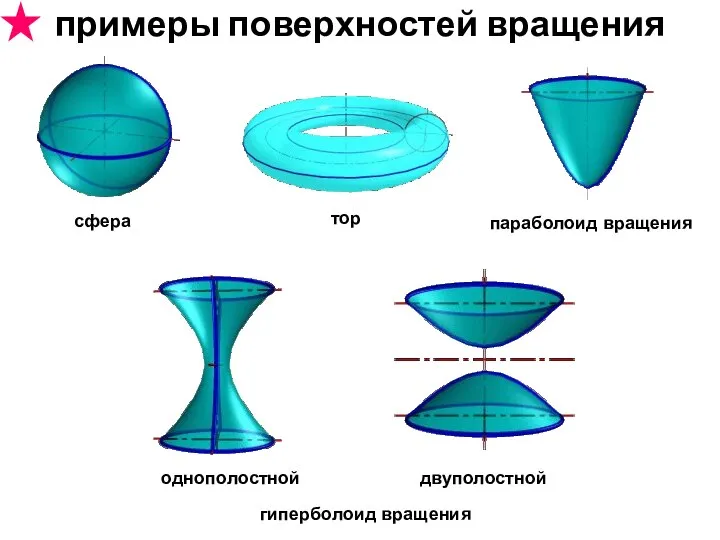
сфера
тор
параболоид вращения
гиперболоид вращения
однополостной
двуполостной
примеры поверхностей вращения

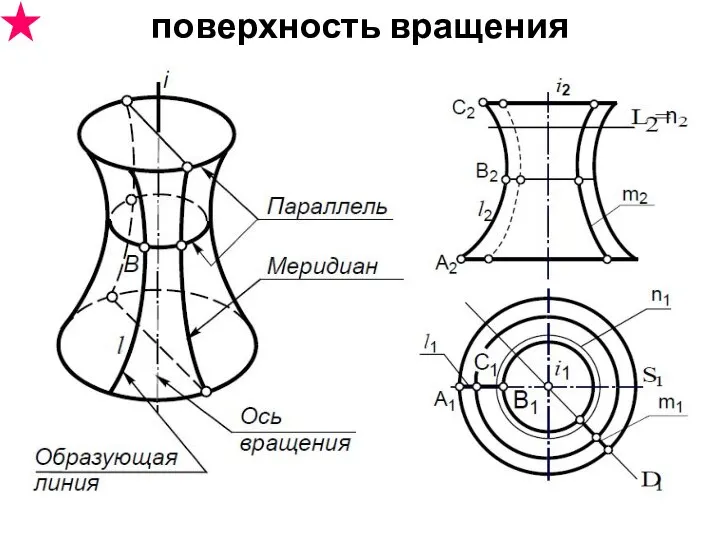
поверхность вращения

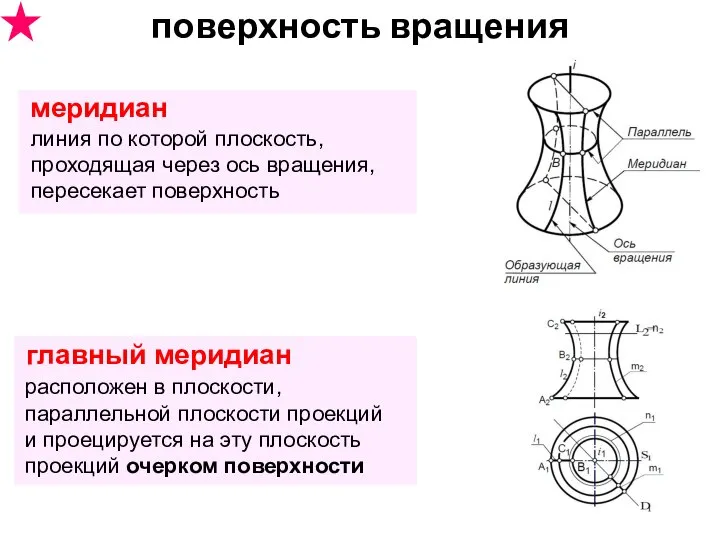
поверхность вращения
меридиан
линия по которой плоскость, проходящая через ось вращения, пересекает поверхность
главный меридиан
расположен в плоскости, параллельной плоскости проекций
и проецируется на эту плоскость проекций очерком поверхности

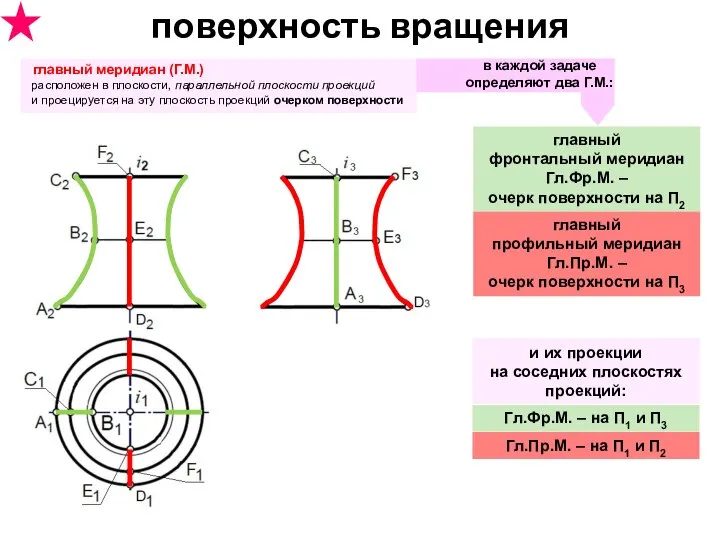
поверхность вращения
главный меридиан (Г.М.)
расположен в плоскости, параллельной плоскости проекций
и проецируется на эту плоскость проекций очерком поверхности
главный
профильный меридиан
Гл.Пр.М. –
очерк поверхности на П3
главный
фронтальный меридиан
Гл.Фр.М. –
очерк поверхности на П2
в каждой задаче определяют два Г.М.:
и их проекции
на соседних плоскостях проекций:
Гл.Фр.М. – на П1 и П3
Гл.Пр.М. – на П1 и П2

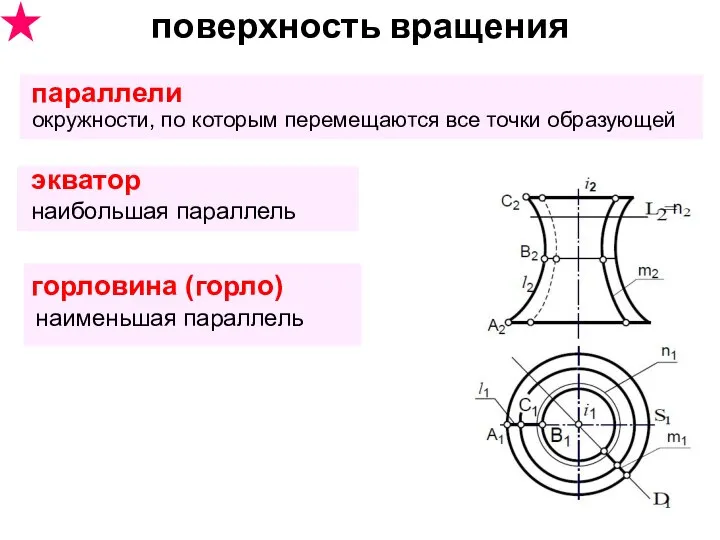
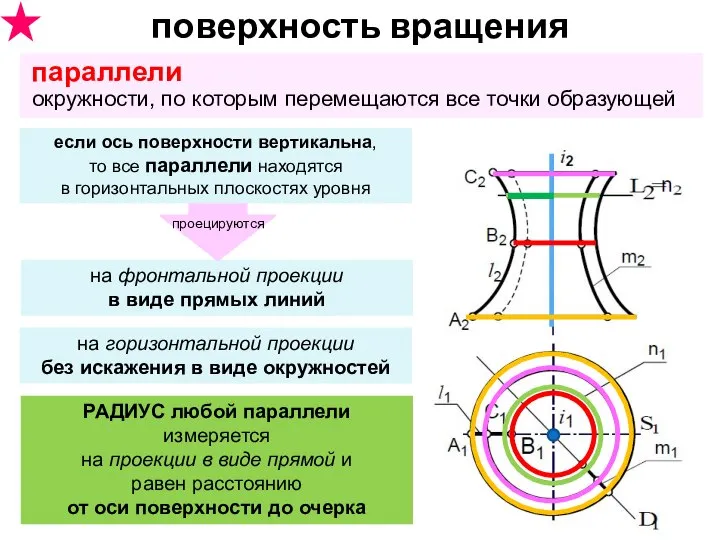
поверхность вращения
параллели
окружности, по которым перемещаются все точки образующей
экватор
наибольшая параллель
горловина (горло)
наименьшая параллель

поверхность вращения
на горизонтальной проекции
без искажения в виде окружностей
на фронтальной проекции
в виде прямых линий
если ось поверхности вертикальна,
то все параллели находятся
в горизонтальных плоскостях уровня
РАДИУС любой параллели измеряется
на проекции в виде прямой и
равен расстоянию
от оси поверхности до очерка

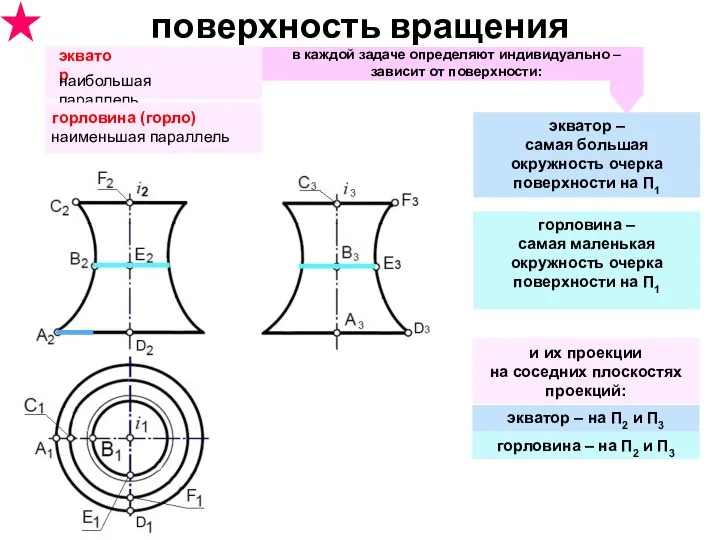
поверхность вращения
горловина –
самая маленькая окружность очерка поверхности на П1
экватор –
самая большая окружность очерка поверхности на П1
в каждой задаче определяют индивидуально – зависит от поверхности:
и их проекции
на соседних плоскостях проекций:
экватор – на П2 и П3
горловина – на П2 и П3

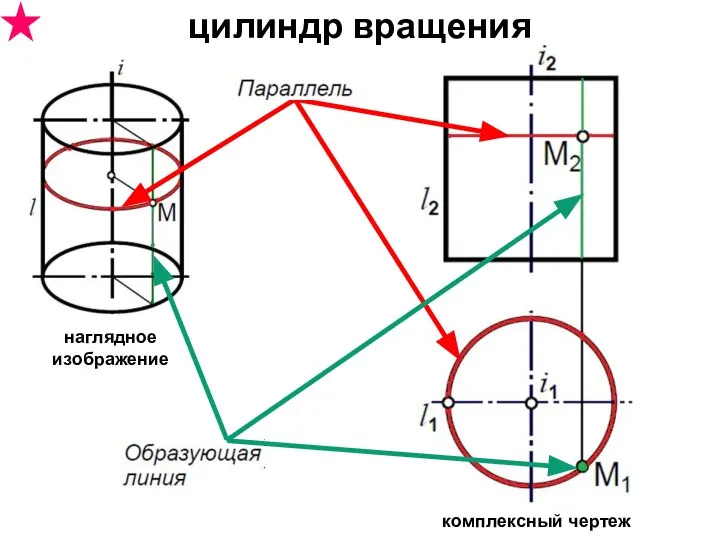
цилиндр вращения
комплексный чертеж
наглядное
изображение

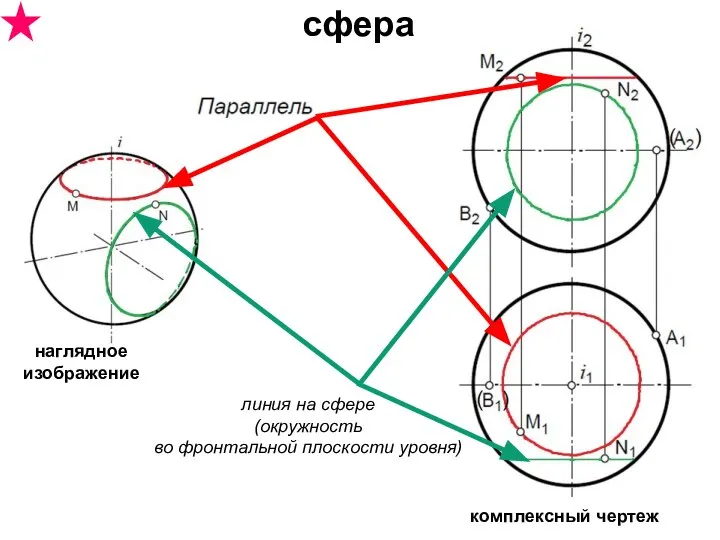
сфера
комплексный чертеж
наглядное
изображение
линия на сфере
(окружность
во фронтальной плоскости уровня)

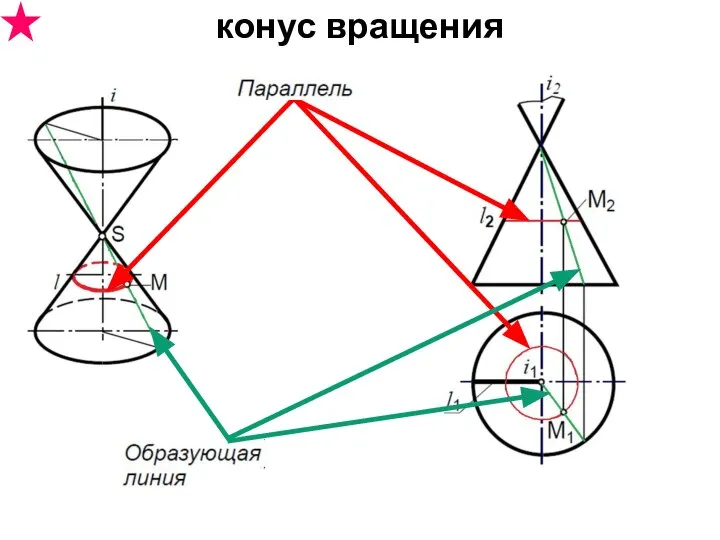
конус вращения

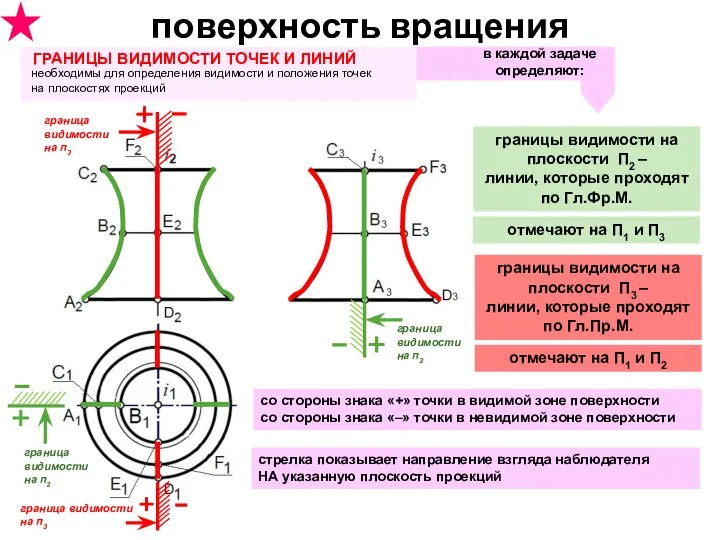
поверхность вращения
ГРАНИЦЫ ВИДИМОСТИ ТОЧЕК И ЛИНИЙ
необходимы для определения видимости и положения точек на плоскостях проекций
в каждой задаче определяют:
границы видимости на плоскости П3 –
линии, которые проходят по Гл.Пр.М.
границы видимости на плоскости П2 –
линии, которые проходят по Гл.Фр.М.
отмечают на П1 и П3
отмечают на П1 и П2
со стороны знака «+» точки в видимой зоне поверхности
со стороны знака «–» точки в невидимой зоне поверхности
стрелка показывает направление взгляда наблюдателя
НА указанную плоскость проекций

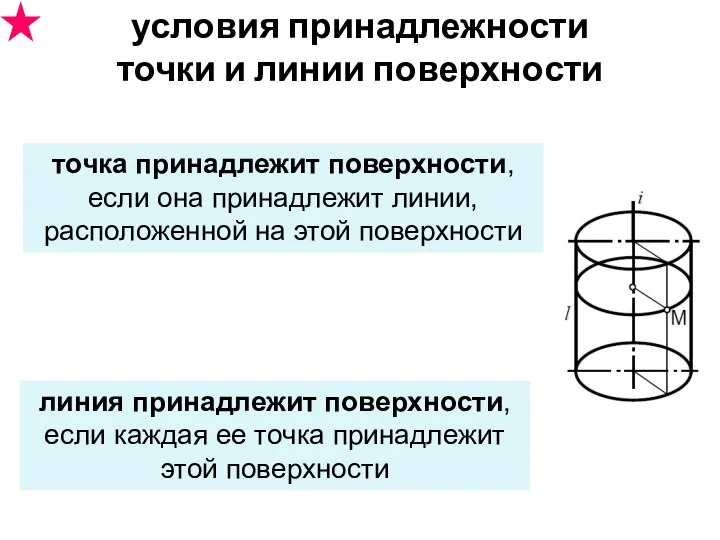
условия принадлежности
точки и линии поверхности
точка принадлежит поверхности,
если она принадлежит линии, расположенной на этой поверхности
линия принадлежит поверхности,
если каждая ее точка принадлежит
этой поверхности

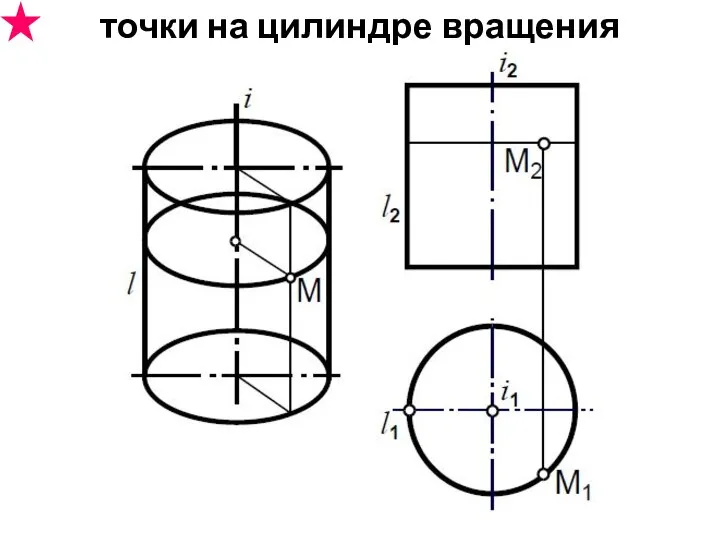
точки на цилиндре вращения

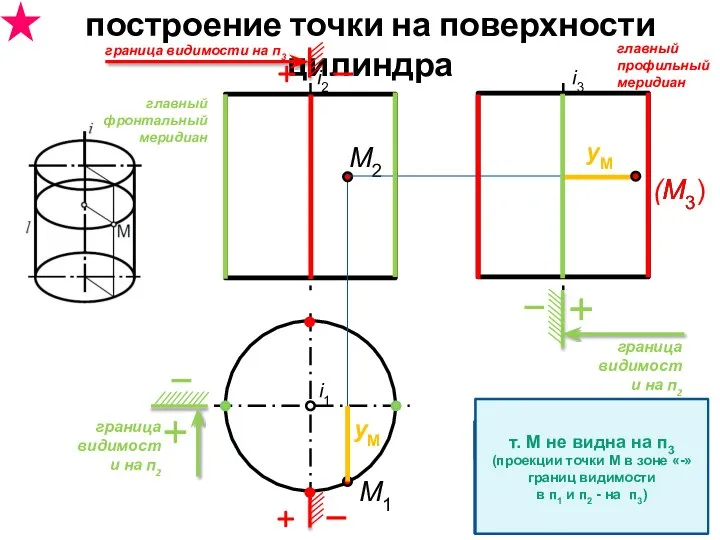
построение точки на поверхности цилиндра
i1
i2
i3
M2
M1
yM
yM
M3
граница видимости на п2
границы видимости
граница видимости на п2
граница видимости на п3
(M3)
главные меридианы
главный
фронтальный
меридиан
главный
профильный
меридиан
провести линию связи вниз на п1 до пересечения с очерком (в виде окружности)
на п1 отмерить координату Y точки М (указанное расстояние циркулем)
провести линию связи вправо на п3
(по высоте точки)
на п3 отложить координату Y точки М (циркулем)
вправо от оси – т.к.
т. М видна на п2
(зона «+» границ видимости
в п3 и п1 - на п2)
т. М не видна на п3
(проекции точки М в зоне «-» границ видимости
в п1 и п2 - на п3)

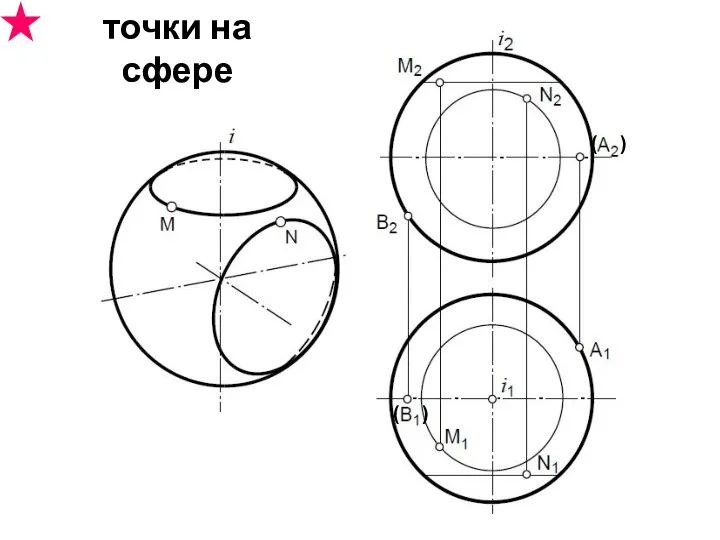
точки на сфере
( )
( )

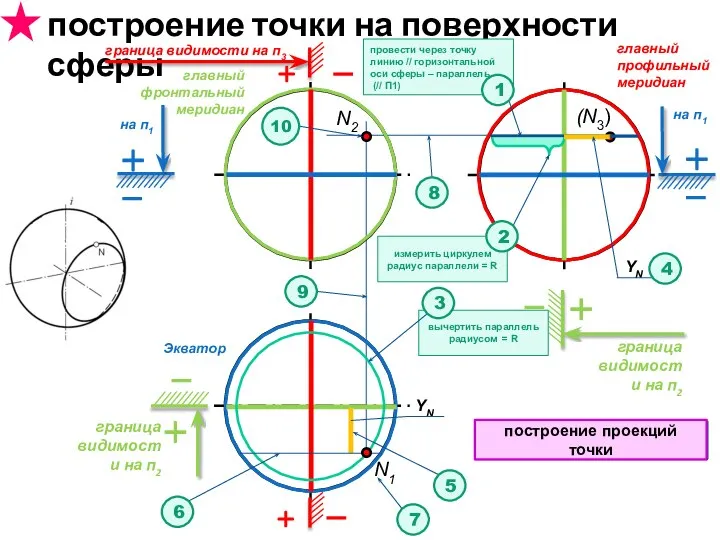
построение точки на поверхности сферы
N1
граница видимости на п2
Границы видимости
граница видимости на п2
граница видимости на п3
(N3)
Главные меридианы
главный
фронтальный
меридиан
главный
профильный
меридиан
Экватор
на п1
на п1
построение проекций точки
N2

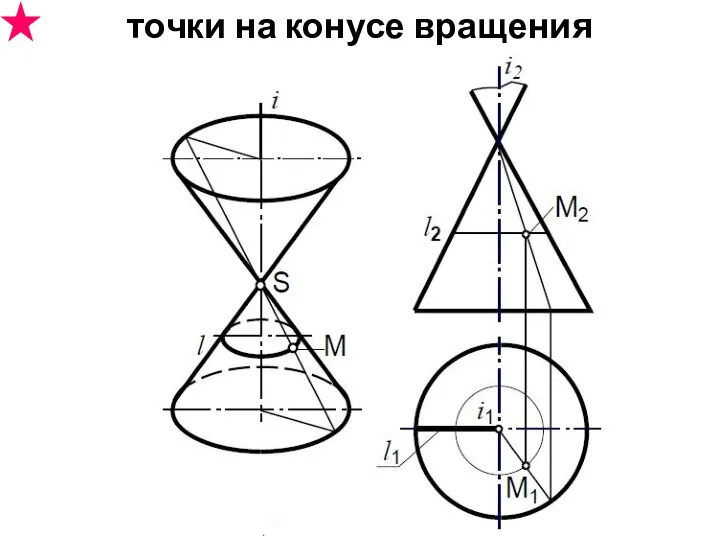
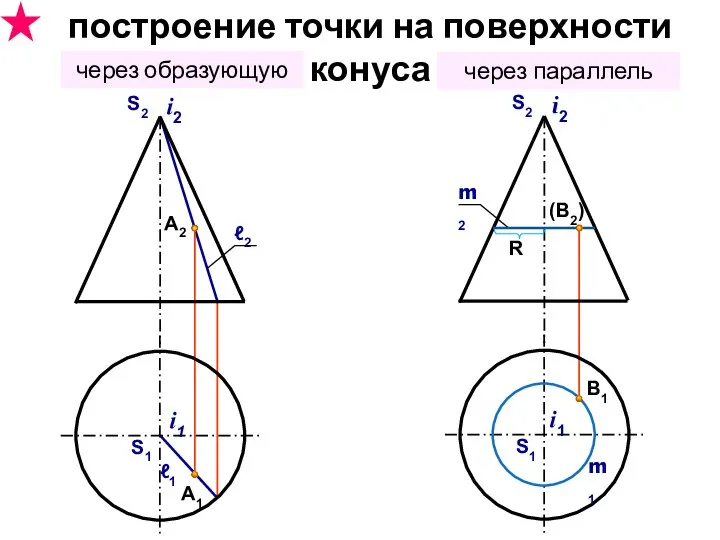
точки на конусе вращения

А2
А1
i2
S2
ℓ2
S1
i1
ℓ1
(B2)
B1
i2
S2
m2
S1
i1
m1
R
построение точки на поверхности конуса
через образующую
через параллель

построить опорные точки
экстремальные точки –
высшая и низшая,
крайняя левая и крайняя правая,
самая далекая и самая ближняя точки кривой
граничные точки видимости кривой,
лежат на очерках поверхности
отделяют видимую часть поверхности от ее невидимой части
алгоритм построения линий на поверхностях
дополнительные точки
1
2
промежуточные точки между опорными
соединить найденные точки
3
определить видимость линии
4