Содержание
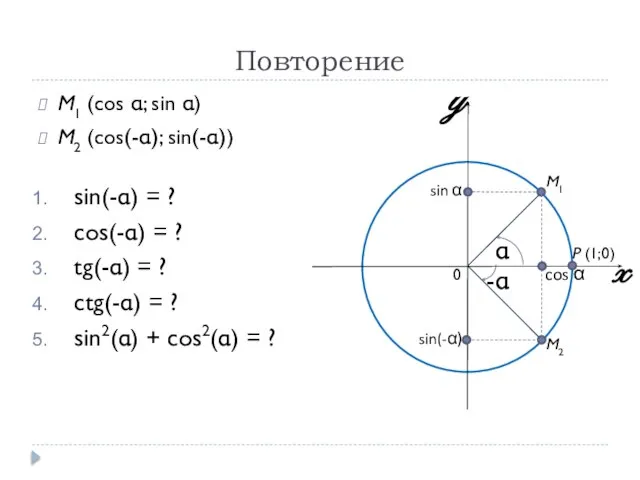
- 2. Повторение M1 (cos α; sin α) M2 (cos(-α); sin(-α)) sin(-α) = ? cos(-α) = ? tg(-α)
- 3. Запишите какой знак имеет выражение:
- 4. Формулы сложения Формулами сложения называют формулы, выражающие cos(α ± β) и sin(α ± β) через косинусы
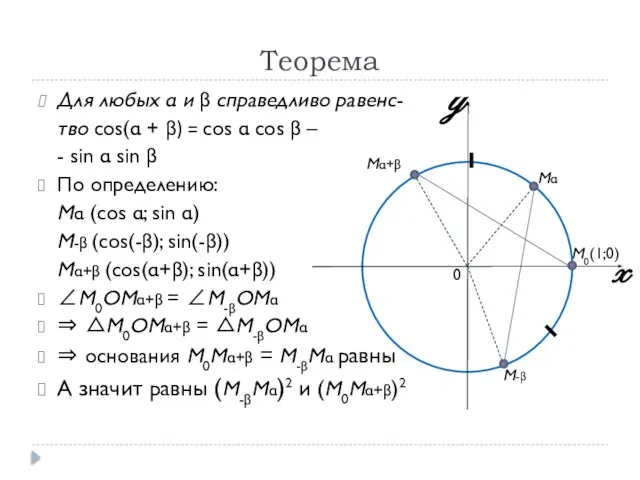
- 5. Теорема Для любых α и β справедливо равенс- тво cos(α + β) = cos α cos
- 6. Теорема Имеем: M0 (1; 0) Mα (cos α; sin α) M-β (cos(-β); sin(-β)) Mα+β (cos(α+β); sin(α+β))
- 7. Следствие 1 cos(α - β) = ? cos(α - β) = cos(α + (-β)) = cos
- 8. Следствие 1 sin(α + β) = cos (π/2 - (α + β)) = cos((π/2 - α)
- 9. Следствие 2 Можно вывести аналогичные формулы для tg(α ± β) и ctg(α ± β). tg(α ±
- 10. Вычислить:
- 11. Вычислить:
- 12. Вычислить:
- 13. Вычислить:
- 15. Скачать презентацию










 Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Вектор. Равенство векторов
Вектор. Равенство векторов Степень, графики функций, пропорции на уроках математики и физики
Степень, графики функций, пропорции на уроках математики и физики Связь деления и умножения
Связь деления и умножения Интегрирование некоторых классов функций. Лекция 2
Интегрирование некоторых классов функций. Лекция 2 Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Математика. 1 класс
Математика. 1 класс Построение графиков функций
Построение графиков функций Площадь фигур
Площадь фигур Уравнение. Правила решения уравнения
Уравнение. Правила решения уравнения Умножение смешанных дробей
Умножение смешанных дробей Площадь геометрических фигур. Задачи
Площадь геометрических фигур. Задачи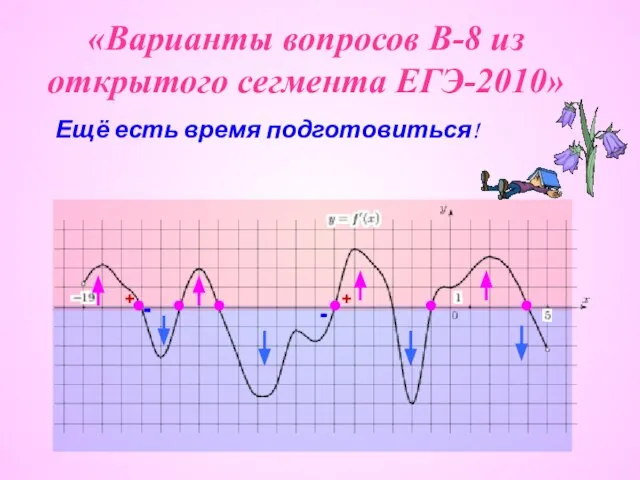 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Критерий Пирсона
Критерий Пирсона Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс Практическая работа
Практическая работа Построение таблиц истинности для логических выражений
Построение таблиц истинности для логических выражений Круг, окружность, длина и площадь окружности
Круг, окружность, длина и площадь окружности Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Вычисли и запомни
Вычисли и запомни Площадь треугольника
Площадь треугольника Применение производной функции для отыскания точек экстремума
Применение производной функции для отыскания точек экстремума Проценты. Часть 2
Проценты. Часть 2 Площадь полной поверхности призмы
Площадь полной поверхности призмы Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника Пирамида
Пирамида Как посчитать консонанс
Как посчитать консонанс