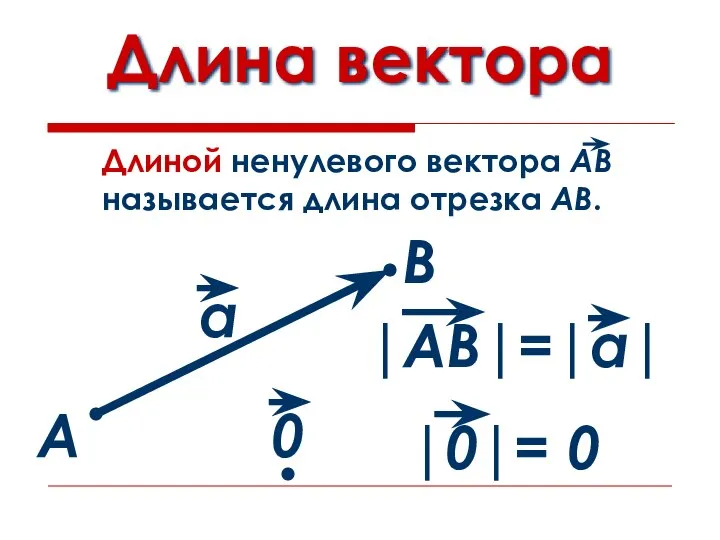
Слайд 2Понятие вектора
А
В
Отрезок, для которого указано, какой из
его концов считается началом,
а какой
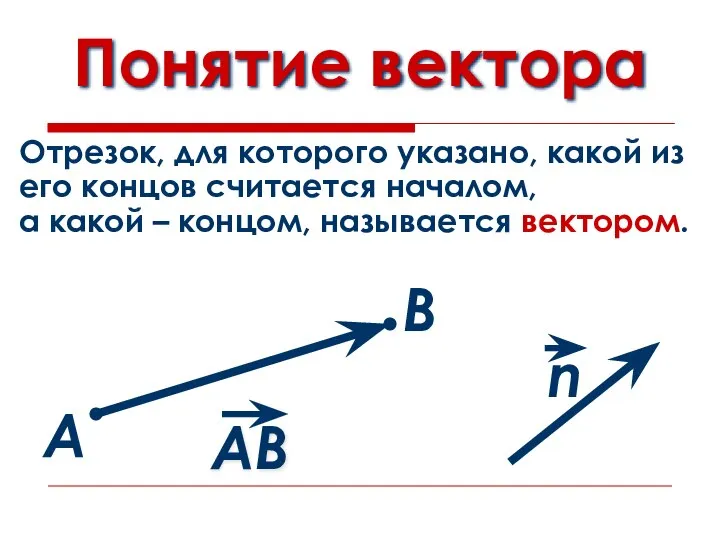
– концом, называется вектором.
Слайд 3Нулевой вектор
Любая точка на плоскости может
рассматриваться как вектор.
М
Такой вектор называется

нулевым.
Слайд 5Коллинеарность векторов
Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой

или на параллельных прямых.
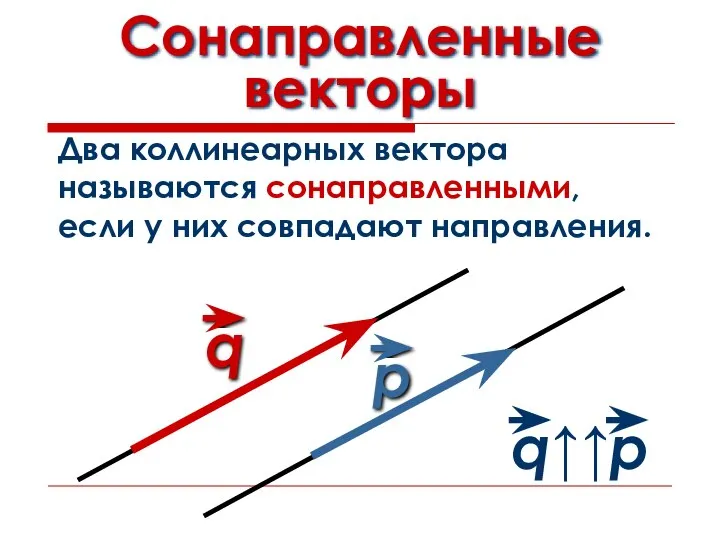
Слайд 6Сонаправленные векторы
Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
Слайд 7Противоположно направленные векторы
Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.

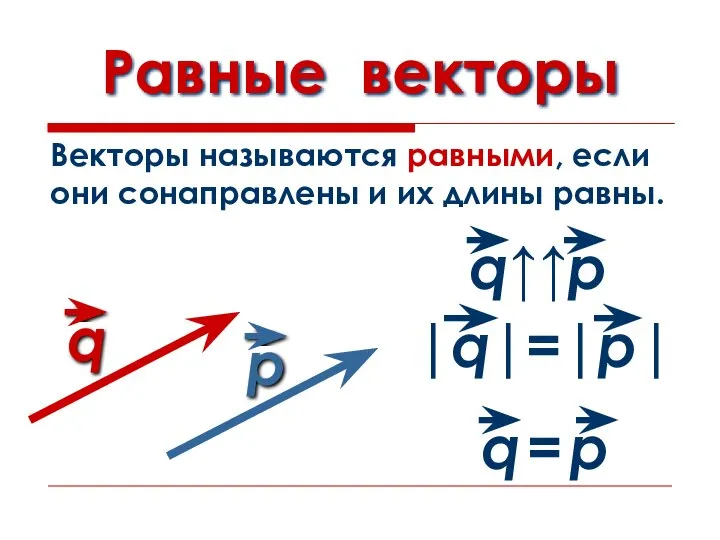
Слайд 8Равные векторы
Векторы называются равными, если
они сонаправлены и их длины равны.
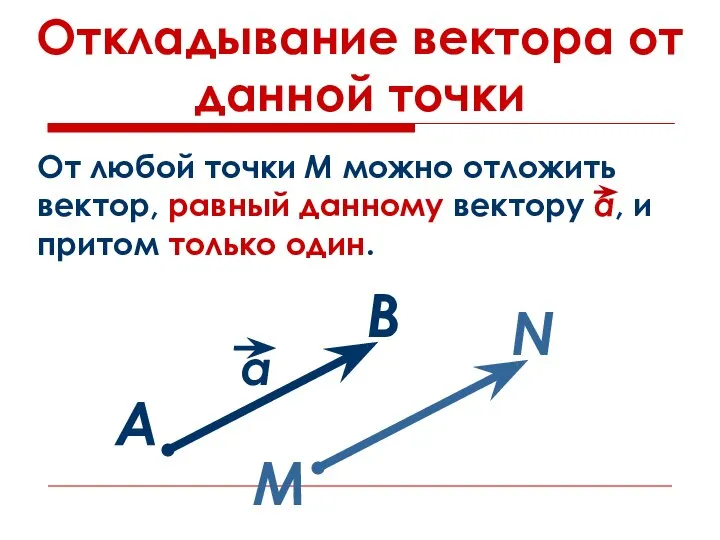
Слайд 9Откладывание вектора от данной точки
А
В
М
N
Слайд 12Домашнее задание:
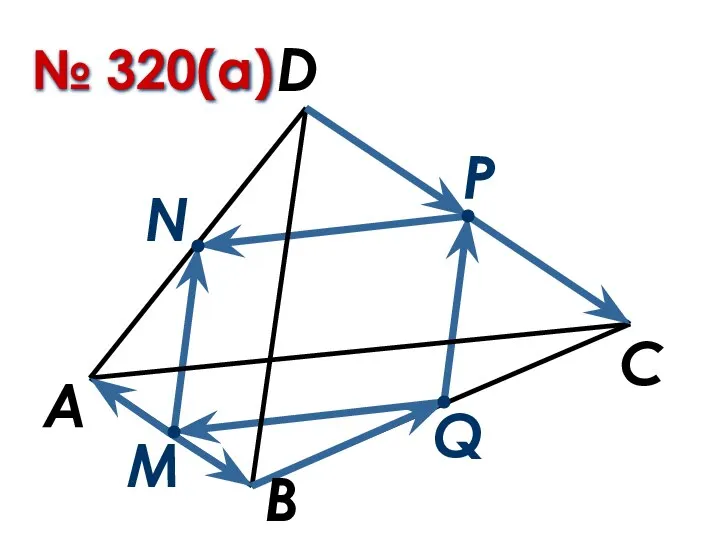
П. 38, 39, № 320(б)










 Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Движение и скорость. Тест
Движение и скорость. Тест Правила теории вероятности
Правила теории вероятности Числа по порялку
Числа по порялку Усеченный конус. Часть 5
Усеченный конус. Часть 5 Системы распознавания образов
Системы распознавания образов Геометрические преобразования
Геометрические преобразования Умножение дробей. Устная работа
Умножение дробей. Устная работа Умножение десятичных дробей
Умножение десятичных дробей Презентация на тему Применение свойств функций к решению уравнений и неравенств
Презентация на тему Применение свойств функций к решению уравнений и неравенств  Понятие вектора
Понятие вектора Урок математики 11.09
Урок математики 11.09 В мире случайных закономерностей. Введение в вероятность. 5 класс
В мире случайных закономерностей. Введение в вероятность. 5 класс Теорема Пифагора (часть 2)
Теорема Пифагора (часть 2) Геометрические преобразования графиков функций
Геометрические преобразования графиков функций Математические ребусы
Математические ребусы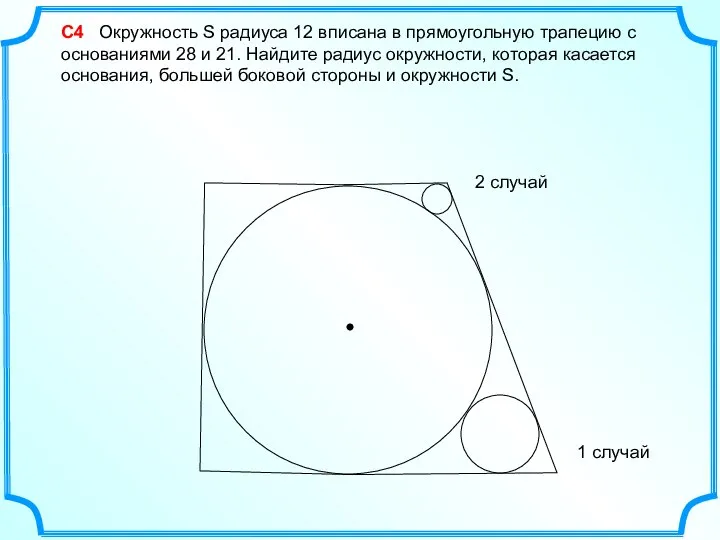 Вписанная окружность. Решение задач
Вписанная окружность. Решение задач Вписанная окружность. Свойство описанного четырехугольника. 8 класс
Вписанная окружность. Свойство описанного четырехугольника. 8 класс Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Анализ результатов диагностики
Анализ результатов диагностики Великолепная пятерка. Игра
Великолепная пятерка. Игра Математический диктант
Математический диктант История системы мер длины (часть 1)
История системы мер длины (часть 1) Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Урок математики 21.09
Урок математики 21.09 Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью