Содержание
- 2. Пусть на промежутке функция задана таблично, а также известны некоторые её производные. Узлы, в которых заданы
- 3. Найти многочлен степени , такой, что: Многочлен Эрмита Утверждение. Многочлен , удовлетворяющий условиям эрмитовой интерполяции, существует
- 4. Доказательство. 1) Единственность (от противного). Пусть существует ещё один многочлен , удовлетворяющий условиям задачи. Найдём их
- 5. 2) Существование. Будем строить алгоритм нахождения многочлена . Что и будет доказательством его существования. Введём узлы
- 7. Выпишем многочлен Ньютона Выразим разделённые разности через производные при Когда т.е.
- 8. Переходя к пределу получим: Пример. Сведения о некоторой функции представлены следующей дискретной информацией:
- 9. Рассчитаем кратности узлов Следует строить многочлен степени
- 11. Для −кратно дифференцируемой функции остаточный член интерполяционного многочлена имеет вид
- 12. Если все узлы простые (однократные), то многочлен Эрмита есть многочлен Лагранжа: Если вся информация об сосредоточена
- 13. Сплайн – интерполяция Кубический сплайн
- 14. Сплайн – некоторая математическая модель гибкого тонкого стержня из упругого материала. Определение. Сплайном называется определённая на
- 15. Прикладное применение. Задача проведения гладкой кривой через точки, произвольным образом лежащие на плоскости, имеет прикладное применение.
- 16. Лаборатория вычисляет координаты по данным, получаемым со спутников GPS (Global Positioning System − глобальной системы позиционирования)
- 17. Примеры сплайнов: Кусочно-линейная функция Степень сплайна – 1, дефект – 1.
- 18. Определение. Кубический сплайн дефекта 1, интерполирующий функцию есть функция удовлетворяющая совокупности условий:
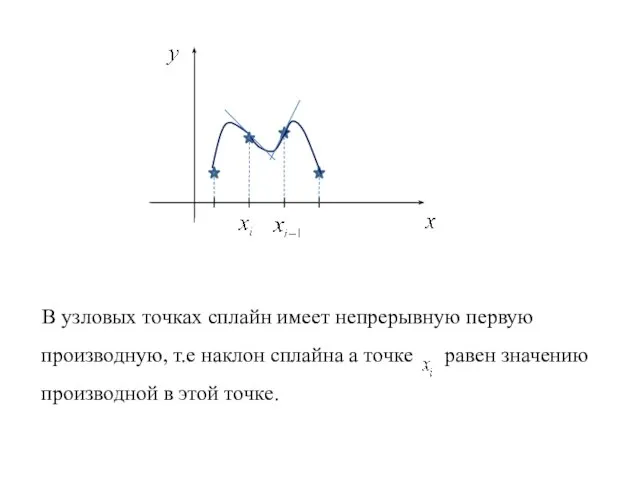
- 19. В узловых точках сплайн имеет непрерывную первую производную, т.е наклон сплайна а точке равен значению производной
- 20. Дано: Найти сплайн Рассмотрим отрезок Вывод: строим интерполяционный многочлен с кратными узлами − кратность 2 −
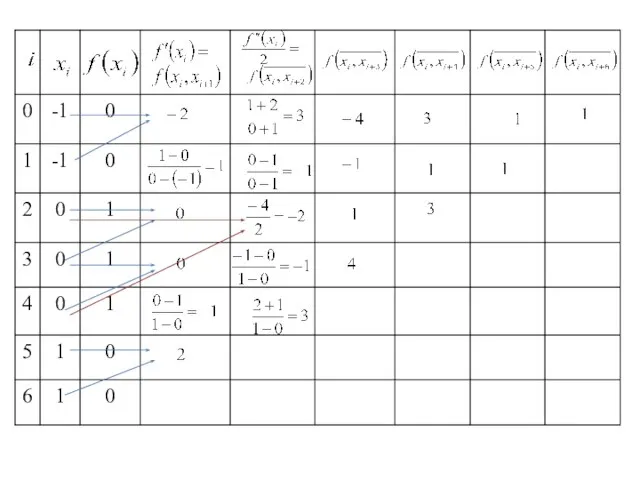
- 21. Составим таблицу разделённых разностей
- 22. Если неизвестны наклоны сплайна (т.е. значения производной в узлах), вычисляют их примерное значение по формулам численного
- 24. Скачать презентацию




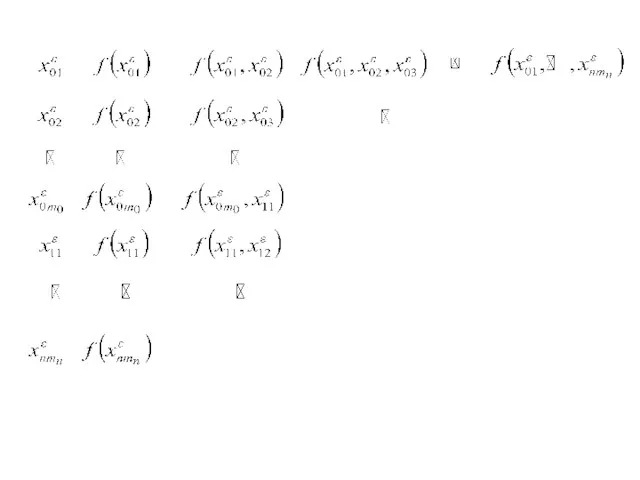














 Планиметрия. Стереометрия
Планиметрия. Стереометрия Правильные многоугольники
Правильные многоугольники Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Урок математики в 1 классе
Урок математики в 1 классе Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Решение квадратного уравнения общего вида
Решение квадратного уравнения общего вида Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Уравнения математической физики
Уравнения математической физики Интегральные уравнения
Интегральные уравнения Критерий Манна-Уитни
Критерий Манна-Уитни Ребусы от тётушки Совы
Ребусы от тётушки Совы Уравнения – это ключ, открывающий все математические сезамы. С.Коваль
Уравнения – это ключ, открывающий все математические сезамы. С.Коваль Соединения с повторениями
Соединения с повторениями Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  формулы сокрощенного умножения
формулы сокрощенного умножения Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест
Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест Упрощение выражений. Тест
Упрощение выражений. Тест Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат В мире цифр. Дидактическое пособие
В мире цифр. Дидактическое пособие Состав чисел первого десятка
Состав чисел первого десятка Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Тригонометрические уравнения
Тригонометрические уравнения Правильные многоугольники
Правильные многоугольники Презентация на тему ГИА 2013. Модуль алгебра №6
Презентация на тему ГИА 2013. Модуль алгебра №6  Сложение, вычитание, умножение,
Сложение, вычитание, умножение,