Решение логических задач

Наиболее распространены три способа решения логических задач:
Средствами алгебры логики
Табличный
С помощью рассуждений

Этапы решения задач средствами алгебры логики
Изучаем условие задачи
Вводим систему обозначений для логических высказываний
Создается логическая формула, описывающая логические связи между всеми условиями задачи
Определяются значения истинности этой логической формулы
Из полученных значений истинности формулы определяются значения истинности введенных логических высказываний, на основании которых делается заключение о решении

Решение задач средствами алгебры логики
ЗАДАЧА
Внимание Андрея, Дениса и Коли привлек промчавшийся мимо автомобиль. Ребята выдвинули три версии:
1. Английская машина «Феррари»
2. Итальянская машина «Понтиак»
3. Машина «Сааб»
Проходящий мимо человек сказал, что каждый из ребят прав только в одном из двух высказываний.
Какой же марки был тот автомобиль?

РЕШЕНИЕ
Введем обозначение для логических высказываний:
А – машина английская;
Ф – «Феррари»;
И – итальянская машина;
П – «Понтиак»;
С – «Сааб».
Из того факта, что каждый из друзей прав в чем-то одном, получаем три истинных составных высказывания:
А · ͞Ф ν ͞А · Ф; И ·͞П ν ͞И·П; ͞А·͞С ν А·С
Перемножаем все эти истинные логические выражения:
(А · ͞Ф ν ͞А · Ф) · (И ·͞П ν ͞И·П) · (͞А·͞С ν АС).

Для решения нужно определить, при каких значениях логических переменных А, И, Ф, П, С это высказывание истинно.
Упростим выражение, т.к машина не может одновременно быть английской и итальянской (А · И=0), также не может одновременно иметь два названия (Ф · С=0; Ф · П=0; П · С=0).
(А · ͞Ф ν ͞А · Ф)·(И·͞П ν ͞И·П)·(͞А·͞С ν АС)=А· ͞Ф·И·͞П· ͞А·͞С ν А· ͞Ф·И·͞П·А·С ν А· ͞Ф· ͞И·П · ͞А· ͞С ν А· ͞Ф· ͞И·П·А·С ν ͞А·Ф·И·͞П·А·͞С ν А·Ф·И·͞П·А·С ν ͞А·Ф ·͞И·П ·͞ ͞А·͞С ν ͞А · Ф ·͞И·П·А ·͞ С=0 ν 0 ν 0 ν 0 ν А · ͞Ф · И ·͞П · ͞А·͞С ν 0 ν 0 ν 0= ͞А · Ф ·И ·͞ П · ͞А·͞С.
Высказывание: ͞А · Ф ·И ·͞ П · ͞А·͞С истинно только при И=1,Ф=1,А=0, П=0, С=0.
ОТВЕТ: машина итальянская марки «Феррари».

Решение задач табличным способом
ЗАДАЧА
В оркестр приняли 3-х музыкантов – Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
Смит – самый высокий
Играющий на скрипке меньше ростом играющего на флейте
Играющие на скрипке и флейте также как и Браун любят пиццу
Когда между альтистом и трубачом возникает ссора, их мирит Смит
Браун не умеет играть на трубе и гобое.
Так же известно, что каждый из музыкантов владеет двумя инструментами.

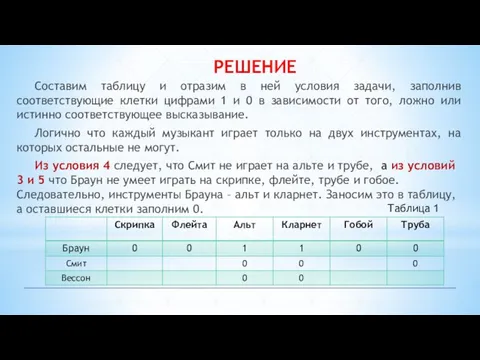
РЕШЕНИЕ
Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 1 и 0 в зависимости от того, ложно или истинно соответствующее высказывание.
Логично что каждый музыкант играет только на двух инструментах, на которых остальные не могут.
Из условия 4 следует, что Смит не играет на альте и трубе, а из условий 3 и 5 что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна – альт и кларнет. Заносим это в таблицу, а оставшиеся клетки заполним 0.
Таблица 1

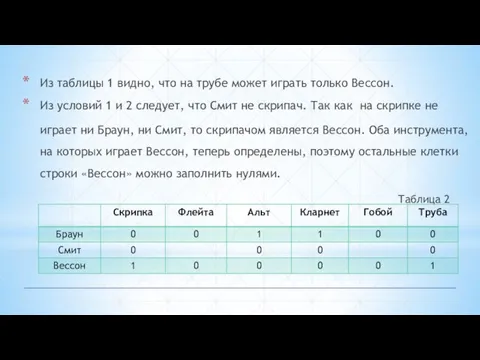
Из таблицы 1 видно, что на трубе может играть только Вессон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки «Вессон» можно заполнить нулями.
Таблица 2

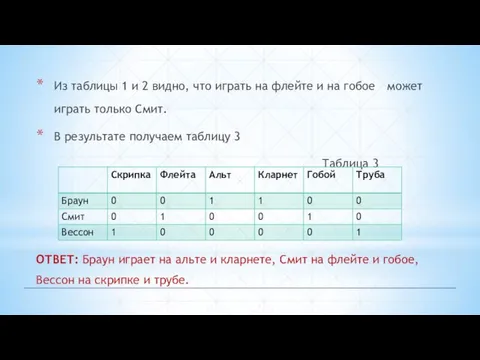
Из таблицы 1 и 2 видно, что играть на флейте и на гобое может играть только Смит.
В результате получаем таблицу 3
Таблица 3
ОТВЕТ: Браун играет на альте и кларнете, Смит на флейте и гобое, Вессон на скрипке и трубе.

Решение логических задач с помощью рассуждений
ЗАДАЧА
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский.
На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский».
Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны.
Какой язык изучает каждый из молодых людей?

РЕШЕНИЕ
Имеется три утверждения:
Сергей не изучает китайский
2. Вадим изучает китайский
3. Михаил не изучает арабский
Если верно первое утверждение, то верно и второе и третье, так как они изучают различные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что двое изучают китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.

Остается считать верным третье утверждение, первое и второе – ложными.
Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
ОТВЕТ: Сергей изучает китайский, Михаил – японский, Вадим – арабский.