Содержание
- 2. Задание 1
- 3. Задание 2
- 4. Рассказ Л.Н. Толстого Много ли человеку земли надо
- 5. Задача 1 Каким должен быть прямоугольник, чтобы его площадь при заданном периметре Р была максимальной. Этапы
- 6. Составление технологической карты решения задач на оптимизацию Задача 1. Какую наибольшую площадь может иметь прямоугольник с
- 7. Составление технологической карты решения задач на оптимизацию Задача 1. Какую наибольшую площадь может иметь прямоугольник с
- 8. Этап 1.
- 9. Этап 2.
- 11. Скачать презентацию




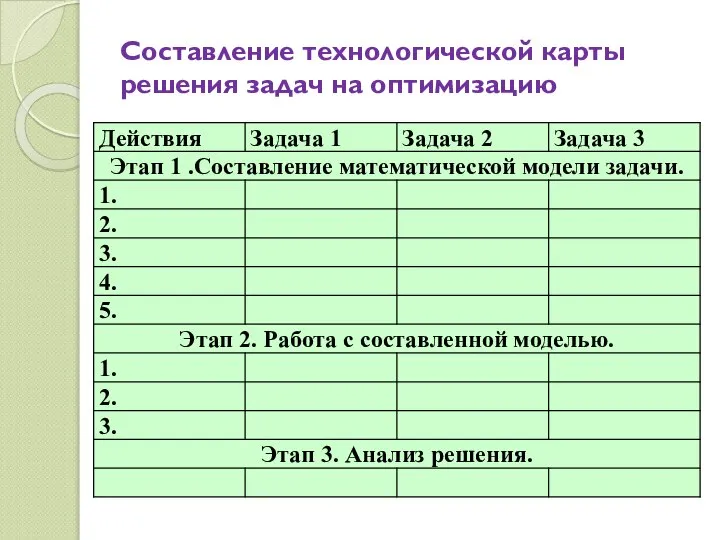
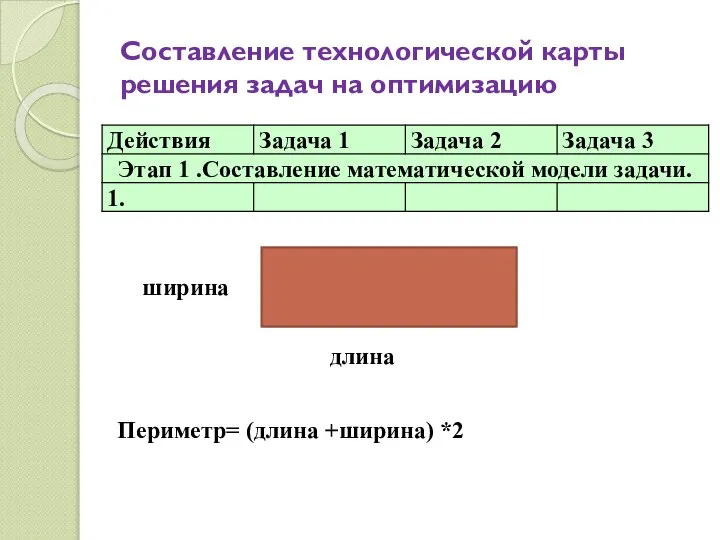

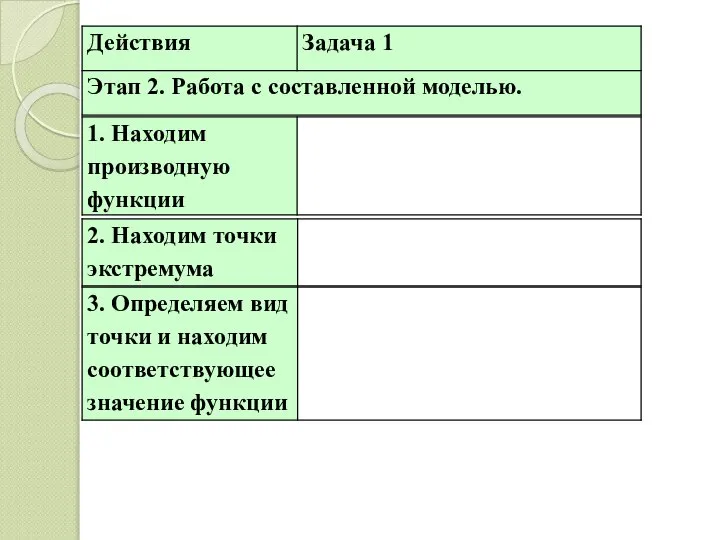
 Схема Горнера. Уильям Джордж Горнер
Схема Горнера. Уильям Джордж Горнер Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА  Рефлексия. Задачи. Домашняя работа
Рефлексия. Задачи. Домашняя работа Урок - игра В мире математики 6 класс
Урок - игра В мире математики 6 класс Элементы математической логики. Теория моделей
Элементы математической логики. Теория моделей Гипербола
Гипербола Прикидка результата. 5 класс
Прикидка результата. 5 класс Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Задачи о дачном участке
Задачи о дачном участке Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры
Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато
Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато Линейная независимость
Линейная независимость Урок математики. Повторение изученного
Урок математики. Повторение изученного Начальное понятие стереометрии. Аксиомы в стереометрии. Тема 8.1 лекция (2ч)!!
Начальное понятие стереометрии. Аксиомы в стереометрии. Тема 8.1 лекция (2ч)!! Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Математическая игра
Математическая игра Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику)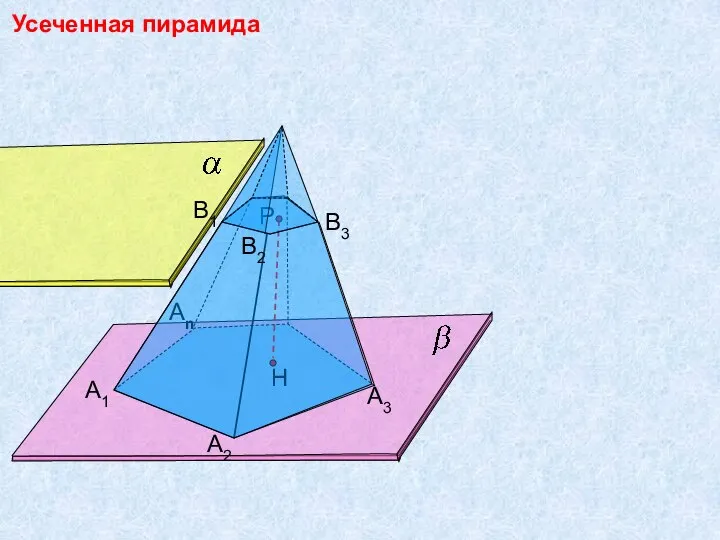 Усеченная пирамида
Усеченная пирамида Математический тренажёр
Математический тренажёр Расстояние между двумя точками (9 класс)
Расстояние между двумя точками (9 класс) Соотношение между сторонами и углами треугольника
Соотношение между сторонами и углами треугольника Степень с целым показателем
Степень с целым показателем График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Эварист Галуа
Эварист Галуа Презентация на тему Подобные слагаемые
Презентация на тему Подобные слагаемые  Исчисление высказываний
Исчисление высказываний Вычитание чисел. Математический тренажер
Вычитание чисел. Математический тренажер Основы функционального анализа
Основы функционального анализа