Парный регрессионный анализ

Уравнение регрессии
Регрессия - математическое выражение, отражающее зависимость зависимой переменной у от независимых переменных х при условии, что это выражение будет иметь статистическую значимость
yˆ = f (x)

ŷ = f (x1,x2,...,xp) – уравнение множественной регрессии
Назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной

линейные и нелинейные регрессии
Линейная регрессия описывается уравнением
yˆ = a + b ⋅ x
Примеры часто используемых нелинейных регрессий

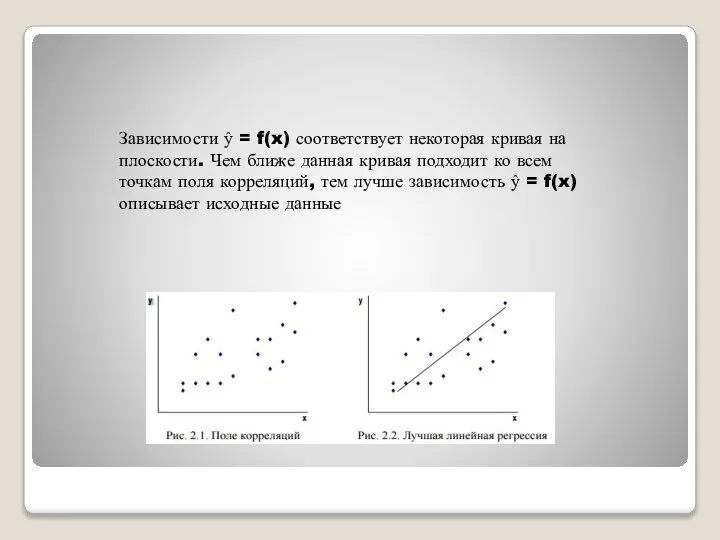
Зависимости ŷ = f(x) соответствует некоторая кривая на плоскости. Чем ближе данная кривая подходит ко всем точкам поля корреляций, тем лучше зависимость ŷ = f(x) описывает исходные данные