Содержание
- 2. Решение тригонометрических неравенств графическим способом Составим алгоритм решения. 1. Если аргумент — сложный (отличен от х),
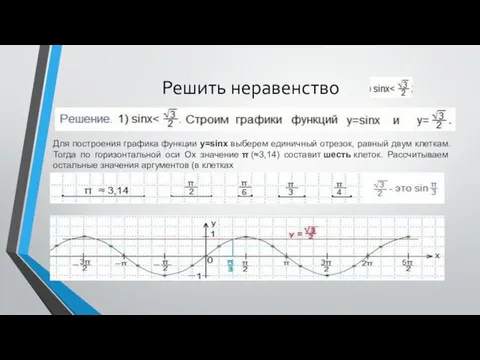
- 3. Решить неравенство Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной
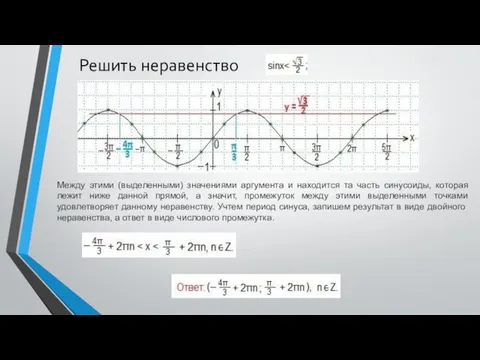
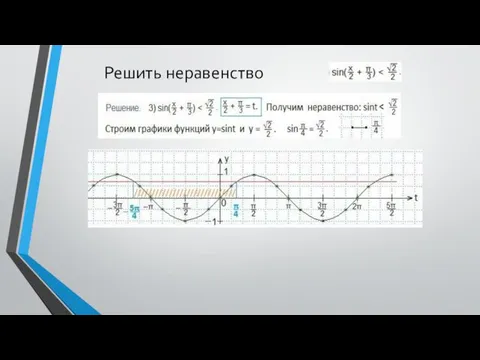
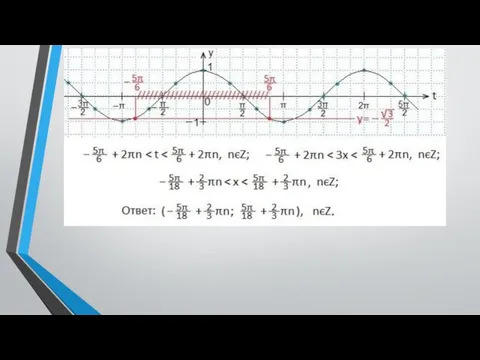
- 4. Решить неравенство Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной
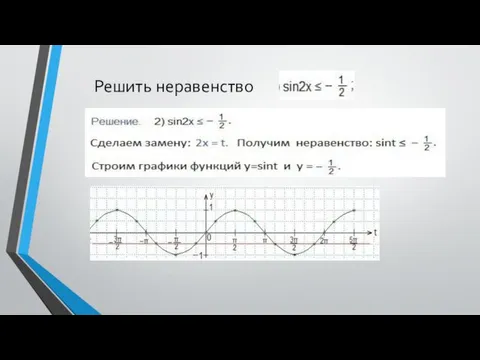
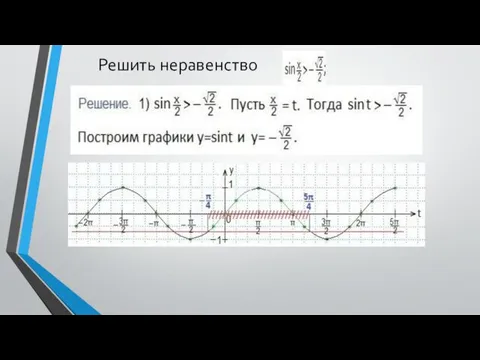
- 5. Решить неравенство
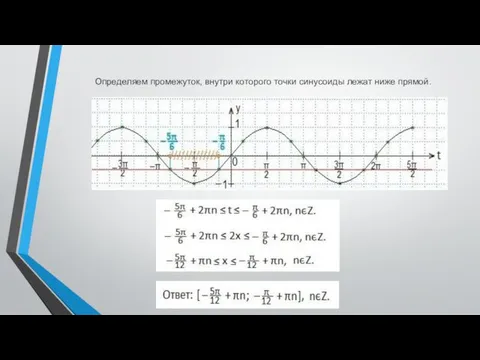
- 6. Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.
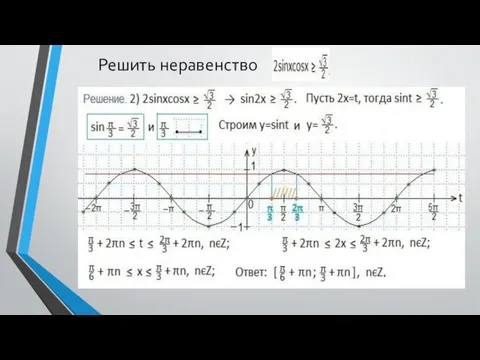
- 7. Решить неравенство
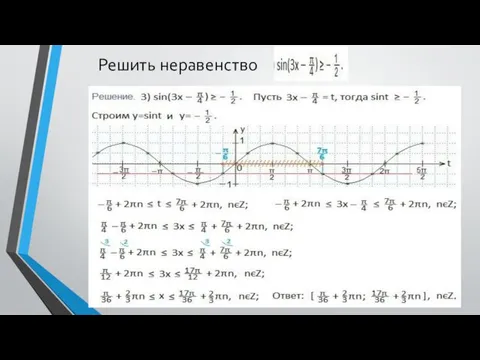
- 9. Решить неравенство
- 11. Решить неравенство
- 12. Решить неравенство
- 13. Решить неравенство
- 15. Решить неравенство
- 17. Решить неравенство
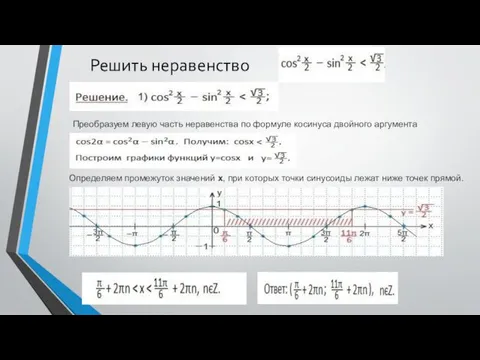
- 19. Решить неравенство Преобразуем левую часть неравенства по формуле косинуса двойного аргумента Определяем промежуток значений х, при
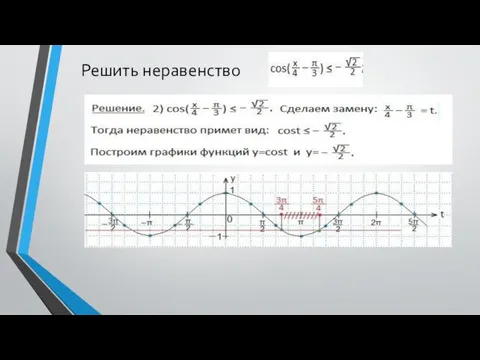
- 20. Решить неравенство
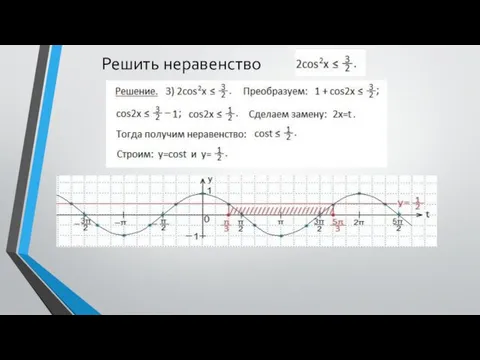
- 22. Решить неравенство
- 24. ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint справедлива формула: — π — arcsin a + 2πn
- 25. Если sint>a, где -1≤a≤1, то arcsin a + 2πn
- 26. Если cost arccos a + 2πn
- 27. - arccos a + 2πn . Если cost>a, (-1≤а≤1), то
- 29. Скачать презентацию














 Возведение в квадрат суммы и разности двух выражений. Тест
Возведение в квадрат суммы и разности двух выражений. Тест Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0  54 задачи на чертежах по планиметрии. Теорема Пифагора
54 задачи на чертежах по планиметрии. Теорема Пифагора Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс
Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс  Я тебя слышу
Я тебя слышу Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Великие математики
Великие математики Преобразование выражений с помощью формул сокращенного умножения
Преобразование выражений с помощью формул сокращенного умножения Производная функции
Производная функции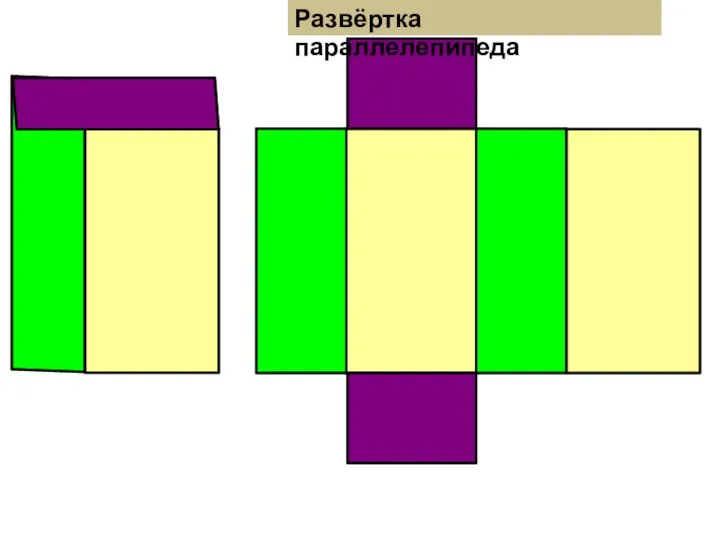 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1)
TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1) Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Нахождение угла между прямой и плоскостью
Нахождение угла между прямой и плоскостью Математико-картографическое моделирование
Математико-картографическое моделирование Презентация на тему Квадратный дециметр (3 класс)
Презентация на тему Квадратный дециметр (3 класс)  Шар и сфера
Шар и сфера ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум
ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс
Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс Легенды о Пифагоре и его теореме
Легенды о Пифагоре и его теореме Математический диктант. Шаблон проверки
Математический диктант. Шаблон проверки Ряды распределения
Ряды распределения Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок
Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Ознакомление с понятием сантиметр
Ознакомление с понятием сантиметр