Содержание
- 2. q = quad (f, a, b) q = quad (f, a, b, tol) q = quad
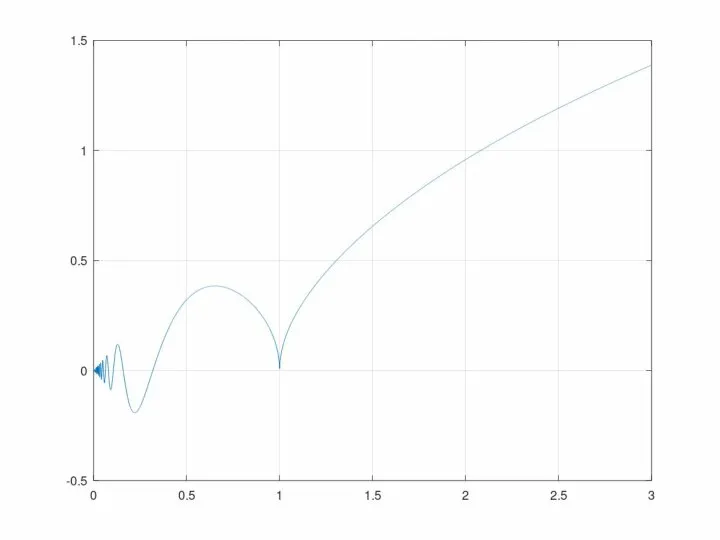
- 3. Вычислить интеграл: Напишем анонимную функцию: f=@(x)x .* sin (1./x) .* sqrt (abs (1 - x)) Построим
- 5. >> f=@(x)x .* sin (1./x) .* sqrt (abs (1 - x)) y=quad(f,0,3) ABNORMAL RETURN FROM DQAGP
- 6. Особенности интегрирования >> f=@(x)x.^-0.9 >> y=quad(f,0,1) y = 9.999999999999792 >> y=quadv(f,0,1) warning: quadv: minimum step size
- 7. Вычислить интеграл: >> f=(@(x) 1 ./ (sqrt (x) .* (x + 1)) >> quadgk(f, 0, Inf)
- 8. Интегрирование таблично заданных функций x=0:0.1:pi/2; y=sin(x); z=trapz (x, y) % Интегрирование методом % трапеций z=0.9966636 Рассмотрим
- 9. Вычисление интеграла с переменным верхним пределом Для вычисления такого интеграла надо составить файл-функцию вида: function y=Fax(f,a,x)
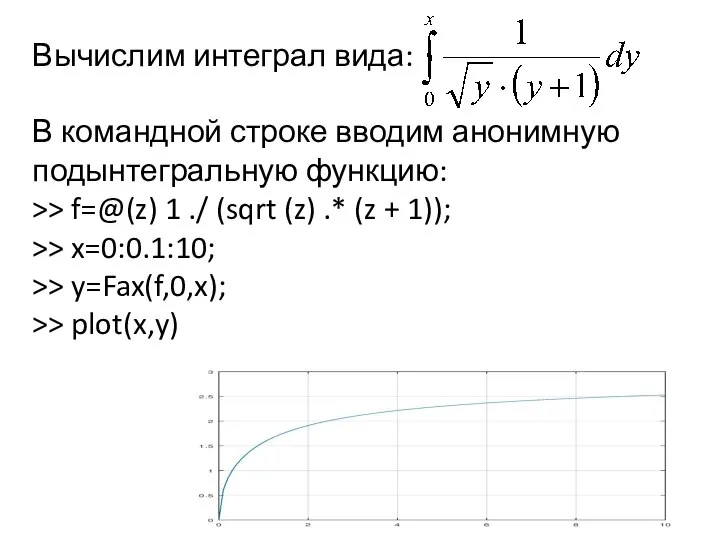
- 10. Вычислим интеграл вида: В командной строке вводим анонимную подынтегральную функцию: >> f=@(z) 1 ./ (sqrt (z)
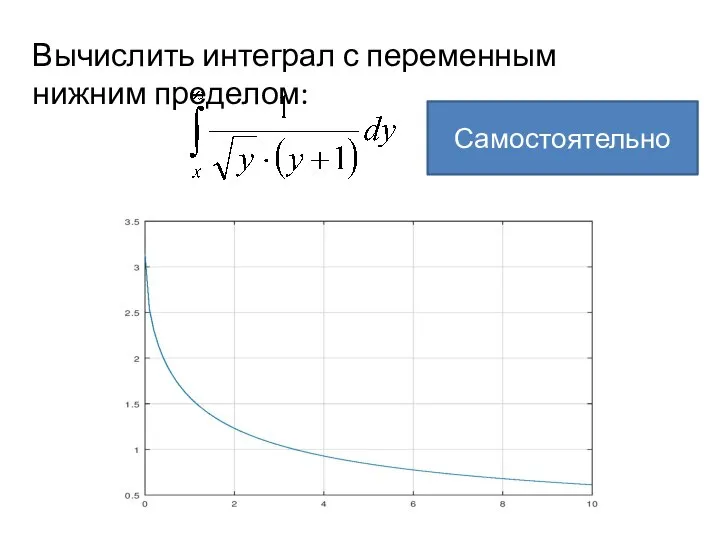
- 11. Вычислить интеграл с переменным нижним пределом: Самостоятельно
- 12. Двумерные интегралы Двумерные интегралы можно вычислять приведением двумерного интеграла к повторному (двумя способами). Особенностями двумерных интегралов
- 13. Вначале напишем функцию, вычисляющую внутренний интеграл по х при различных значениях y: function q = gint(y,a,b)
- 14. В командной строке найдем двумерный интеграл: >> ggint=@(x)gint(x,2,3);In=quadgk(ggint,0,1) In = 0.045377 Этот алгоритм осуществлен в функции
- 15. dblquad (f, xa, xb, ya, yb) dblquad (f, xa, xb, ya, yb, tol) dblquad (f, xa,
- 16. Примеры различных вызовов функции dblquad: >> f=@(x,y)sin(pi*x.*y).*sqrt(x.*y); >> format long; >> In=dblquad (f, 2, 3, 0,
- 17. Рекурсивный алгоритм для интегрирования, представленный выше, называется повторным интегрированием. Существует отдельный двумерный метод интегрирования, который осуществлен
- 18. q = quad2d (f, xa, xb, ya, yb) q = quad2d (f, xa, xb, ya, yb,
- 19. >> f=@(x,y)sin(pi*x.*y).*sqrt(x.*y); >> In=quad2d(f,2,3,0,1) In = 4.537731177584814e-02 Рассмотрим интегрирование по области в двумерном пространстве: y 0.5
- 20. Задание для самостоятельной работы Пусть необходимо построить график функции, которая задается следующей формулой: Собственные значения и
- 21. Исходные данные N=16 f1=0:1023 f2=0:7 T=0.002 df1=1 df2=3 P=1000 Выдать промежуточные данные: Построить график N/2 –й
- 23. Скачать презентацию

















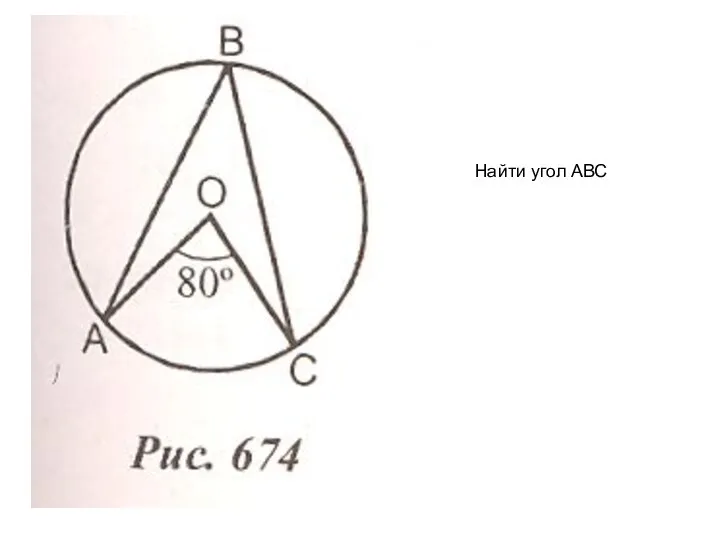 Найти угол АВС
Найти угол АВС Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Применение производной. Задание 8 (профильный уровень)
Применение производной. Задание 8 (профильный уровень) Урок математики
Урок математики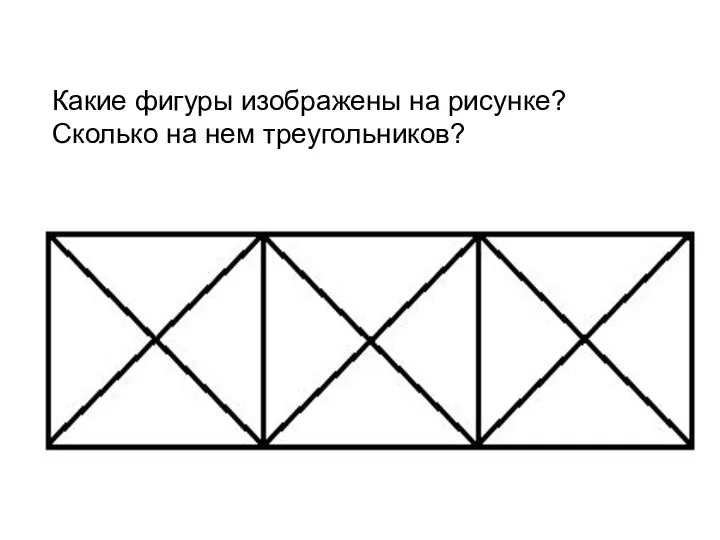 Периметр треугольника
Периметр треугольника Иерархическая кластеризация
Иерархическая кластеризация Проценты чисел
Проценты чисел Подмножество. Операции над множествами. Самостоятельная работа
Подмножество. Операции над множествами. Самостоятельная работа Пропорция
Пропорция Násobíme a delíme s Mimoňmi
Násobíme a delíme s Mimoňmi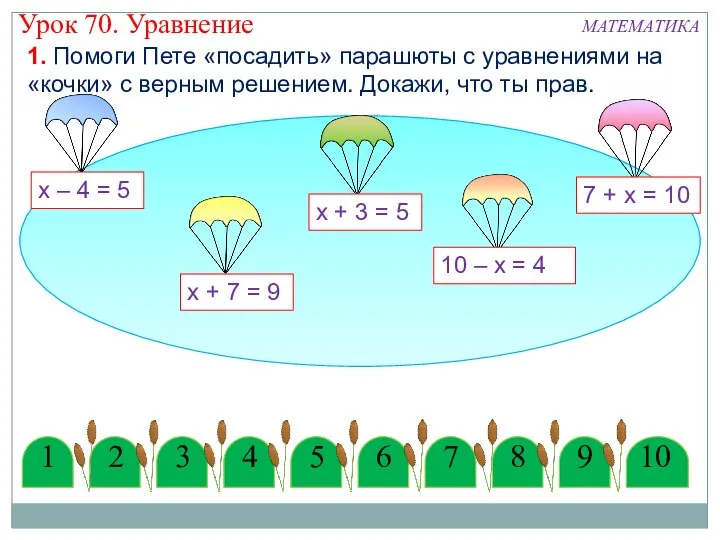 Уравнение. Математика. Урок 70
Уравнение. Математика. Урок 70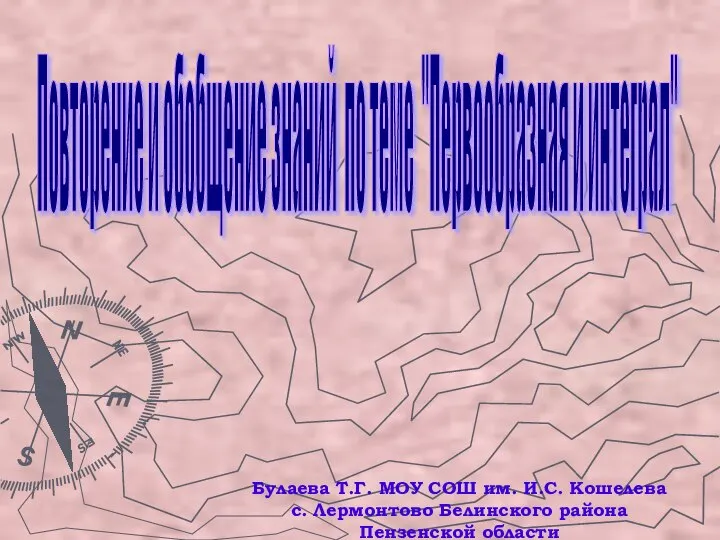 Первообразная и интеграл
Первообразная и интеграл Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Преобразование формул
Преобразование формул Дополнительные задачи. 7 класс
Дополнительные задачи. 7 класс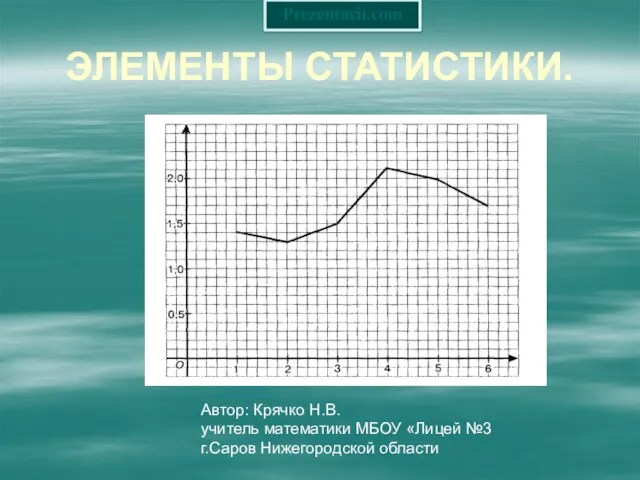 Презентация на тему Элементы статистики
Презентация на тему Элементы статистики  Шкала. Координатный луч
Шкала. Координатный луч 08.09
08.09 Производная вокруг нас
Производная вокруг нас Длина ломанной
Длина ломанной Введение в теорию графов
Введение в теорию графов Геометрические фигуры
Геометрические фигуры Проценты. Ж.Ж. Руссо (1712–1778 гг.)
Проценты. Ж.Ж. Руссо (1712–1778 гг.) Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Разложение многочлена на множители с помощью формулы сокращенного умножения
Разложение многочлена на множители с помощью формулы сокращенного умножения Один - много. 1 класс
Один - много. 1 класс Статистика и ее роль в развитии общества
Статистика и ее роль в развитии общества Правильные многоугольники
Правильные многоугольники